Unit outcomes

By the end of this unit you will be able to:

• Define Coulomb’s law.
• Apply Coulomb’s law to calculate the force between charges.

What you should know

Before you start this unit, make sure you can:

• Describe how objects become charged. You can refer to level 2, subject outcome 4.2, unit 1 to revise this.
• Describe how charged objects interact. You can refer to level 2, subject outcome 4.2, unit 2 to revise this.
• Find the resultant of vectors. You can refer to level 2, subject outcome 4.2, unit 4 to revise this.

Introduction

Parts of the text in this unit were sourced from Siyavula Physical Science Gr 11 Learner’s Book, Chapter 9, released under a CC-BY licence

You know that charged objects exert forces on each other and that the rule of electrostatics is ‘like charges repel and unlike charges attract’. In this unit you will learn about the factors that determine the strength of this electrostatic force and how to calculate the force.

Measuring charge

You know that objects become charged by gaining or losing electrons. The number of electrons lost or gained will determine how charged the object is. The unit in which charge is measured is called a coulomb (C). One coulomb is a very large charge. In electrostatics we therefore often work with charges in micro-coulombs ([latex]\scriptsize 1\text{ }\mu \text{C}=1\text{ x }{{10}^{{-6}}}\text{C}[/latex]) and nanocoulombs ([latex]\scriptsize 1\text{ }n\text{C}=1\text{ x }{{10}^{{-9}}}\text{C}[/latex]).

Coulomb’s law

The electrostatic force between charges increases when the magnitude (size) of the charges increases or the distance between the charges decreases.

The electrostatic force was first studied in detail by Charles-Augustin de Coulomb around 1784. Through his observations he was able to show that the magnitude of the electrostatic force between two point charges is inversely proportional to the square of the distance between the charges ([latex]\scriptsize F\alpha \displaystyle \frac{1}{{{{r}^{2}}}}[/latex]). He also discovered that the magnitude of the force is proportional to the product of the charges ([latex]\scriptsize F\alpha {{Q}_{1}}{{Q}_{2}}[/latex]). Using the results of his observations he derived the following formula to calculate the electrostatic force between two charged objects:

[latex]\scriptsize F=\displaystyle \frac{{k{{Q}_{1}}_{{}}{{Q}_{2}}}}{{{{r}^{2}}}}[/latex]
Where:
[latex]\scriptsize F[/latex] is the electrostatic force (in N)
[latex]\scriptsize k[/latex] is the electrostatic constant ([latex]\scriptsize 9\text{ x }{{10}^{9}}\text{ N}\text{.}{{\text{m}}^{2}}.{{\text{C}}^{{-2}}}[/latex])
[latex]\scriptsize {{Q}_{1}}\text{ and }{{Q}_{2}}[/latex] are the charges on each object (in coulombs)
[latex]\scriptsize r[/latex] is the distance between the centres of the charges (in m)

Coulomb’s law is defined as follows:

The following example demonstrates how to solve a problem using Coulomb’s Law.

Example 1.1

Study the arrangement of charges below and answer the questions that follow.

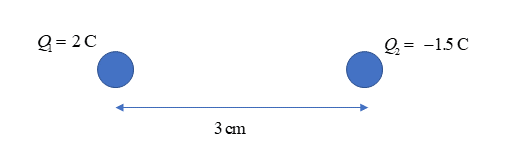
1. What is the magnitude and direction of the force exerted by [latex]\scriptsize {{Q}_{2}}[/latex] on [latex]\scriptsize {{Q}_{1}}[/latex]?
2. What is the magnitude and direction of the force exerted by [latex]\scriptsize {{Q}_{1}}[/latex] on [latex]\scriptsize {{Q}_{2}}[/latex]?

Solutions

Step 1: Write down the given information and what is being asked for in the questions

[latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{2}\text{.0 C}\\{{Q}_{2}}&=\text{1}.5\text{ C}\\r&=\text{3 cm}\\F&=\text{?}\end{align*}[/latex] (there is no need to use [latex]\scriptsize +[/latex] and [latex]\scriptsize -[/latex] signs for charges at this stage)

Step 2: Check units and convert if necessary

[latex]\scriptsize r=\text{ 3 cm = 0}\text{.03 m}[/latex]

Step 3: Write down the formula

[latex]\scriptsize F=\displaystyle \frac{{k{{Q}_{1}}_{{}}{{Q}_{2}}}}{{{{r}^{2}}}}[/latex]

Step 4: Substitute the values into the formula and calculate the answer

[latex]\scriptsize F=\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(2.0)(1.5)}}{{{{{0.03}}^{2}}}}\text{ = 3 x 1}{{\text{0}}^{{13}}}\text{ N}[/latex]

Step 5: Look at the signs of the charges to determine the direction of the force

[latex]\scriptsize {{Q}_{1}}[/latex] is positive and [latex]\scriptsize {{Q}_{2}}[/latex] is negative. Opposite charges attract. Therefore the force exerted by [latex]\scriptsize {{Q}_{2}}[/latex] on [latex]\scriptsize {{Q}_{1}}[/latex] will be to the right.

Step 6: Write the answers with magnitude and direction

1. The force exerted by [latex]\scriptsize {{Q}_{2}}[/latex] on [latex]\scriptsize {{Q}_{1}}[/latex] will be [latex]\scriptsize \text{3 x 1}{{\text{0}}^{{13}}}\text{ N}[/latex] to the right.
2. The force on charge [latex]\scriptsize {{Q}_{2}}[/latex] is equal and opposite to the force on charge [latex]\scriptsize {{Q}_{1}}[/latex]. Therefore the force on charge [latex]\scriptsize {{Q}_{2}}[/latex] is [latex]\scriptsize \text{3 x 1}{{\text{0}}^{{13}}}\text{ N}[/latex] to the left.

Example 1.2

A charged object of [latex]\scriptsize 1.6\text{ }\mu \text{C}[/latex] experiences a force of [latex]\scriptsize 7\text{ }200\text{ N}[/latex] to the right when it is placed [latex]\scriptsize 2\text{ mm}[/latex] to the left of an unknown charge [latex]\scriptsize Q[/latex]. What is the charge on [latex]\scriptsize Q[/latex]?

Solution

Step 1: Write down the given information and what is being asked for in the question

[latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{1}\text{.6 }\mu \text{C}\\r&=\text{2 mm}\\F&=\text{7 200 N}\\{{Q}_{2}}&=\text{?}\end{align*}[/latex]

Step 2: Check the units and convert if necessary

[latex]\scriptsize \begin{align*}r&=\text{ 2 mm = 0}\text{.002 m}\\{{Q}_{1}}&=\text{1}\text{.6 }\mu \text{C = 1}\text{.6 x 1}{{\text{0}}^{{-6}}}\text{ C}\end{align*}[/latex]

Step 3: Write down the formula

[latex]\scriptsize F=\displaystyle \frac{{k{{Q}_{1}}_{{}}{{Q}_{2}}}}{{{{r}^{2}}}}[/latex]

Step 4: Substitute the values and calculate the answer

[latex]\scriptsize \begin{align*}7\text{ 200}&=\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(1.6\text{ x 1}{{\text{0}}^{{-6}}}){{Q}_{2}}}}{{{{{0.002}}^{2}}}}\text{ }\\{{Q}_{2}}&=\text{ 2 x 1}{{\text{0}}^{{-6}}}\text{ C}\end{align*}[/latex]

Step 5: Determine whether the unknown charge has a positive or negative charge from the direction of the force given in the question

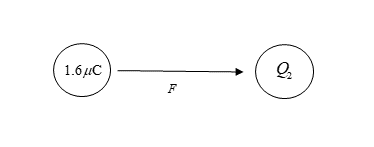
Force is attraction, therefore [latex]\scriptsize {{Q}_{2}}[/latex] must have the opposite charge to [latex]\scriptsize {{Q}_{1}}[/latex]. So, it must be negative.

Step 6: Write the answer with magnitude and sign

The unknown charge is [latex]\scriptsize -2\text{ x 1}{{\text{0}}^{{-6}}}\text{ C}[/latex].

Summary

In this unit you have learnt the following:

• Charge is measured in the units called coulombs (C).
• Coulomb’s law states that the electrostatic force between two point charges is directly proportional to the product of the magnitude of the charges (in coulombs) and inversely proportional to the square of the distance between their centres.
• The magnitude of the force [latex]\scriptsize F[/latex] between point charges [latex]\scriptsize {{Q}_{1}}[/latex] and [latex]\scriptsize {{Q}_{2}}[/latex] that are a distance [latex]\scriptsize r[/latex] apart, can be found using Coulomb’s law, which you can write mathematically as:
  [latex]\scriptsize F=\displaystyle \frac{{k{{Q}_{1}}_{{}}{{Q}_{2}}}}{{{{r}^{2}}}}[/latex] where [latex]\scriptsize k=9\text{ x 1}{{\text{0}}^{9}}\text{ N}\text{.}{{\text{m}}^{2}}.{{\text{C}}^{{-2}}}[/latex].
• The magnitude of the force on each charge will be equal but opposite in direction.
• The direction of the force can be determined by applying the law of electrostatics: like charges repel and unlike charges attract.

Unit 1: Assessment

Suggested time to complete: 40 minutes

1. Study the arrangement of charges in the diagram and answer the questions that follow:
   
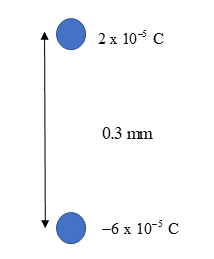
   1. Find the magnitude and the direction of the force on the [latex]2\text{ x 1}{{\text{0}}^{{-5}}}\text{ C}[/latex] charge.
   2. Find the magnitude and the direction of the force on the [latex]\scriptsize -6\text{ x 1}{{\text{0}}^{{-5}}}\text{ C}[/latex] charge.
2. Study the arrangement of charges in the diagram and answer the question.
   
   .
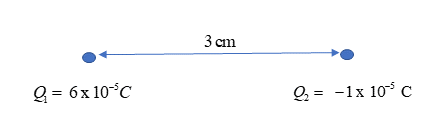
   Calculate the magnitude and direction of the force that charge [latex]\scriptsize {{Q}_{1}}[/latex] experiences.
3. Two point charges of [latex]\scriptsize +3\text{ x 1}{{\text{0}}^{{-9}}}\text{ C}[/latex] and [latex]\scriptsize +5\text{ x 1}{{\text{0}}^{{-9}}}\text{ C}[/latex] are [latex]\scriptsize 2\text{ mm}[/latex]. Determine the magnitude of the force between them and state whether it is attractive or repulsive.
4. Calculate the distance between two charges of [latex]\scriptsize +4\text{ nC}[/latex] and [latex]\scriptsize -3\text{ nC}[/latex] if the electrostatic force between them has a magnitude of [latex]\scriptsize 0.005\text{ N}[/latex].
5. Three point charges are in a straight line as illustrated below. The distances between the charges are given.
   
   .
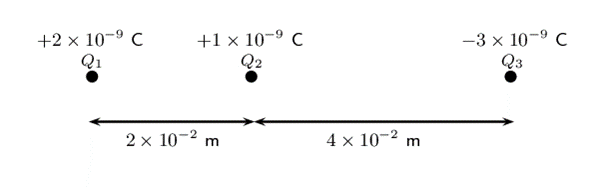
   Calculate the resultant force on [latex]\scriptsize {{Q}_{2}}[/latex].
6. Three point charges, [latex]\scriptsize {{Q}_{1}}[/latex], [latex]\scriptsize {{Q}_{2}}[/latex] and [latex]\scriptsize {{Q}_{3}}[/latex], form a right-angled triangle as illustrated below:
   
   .
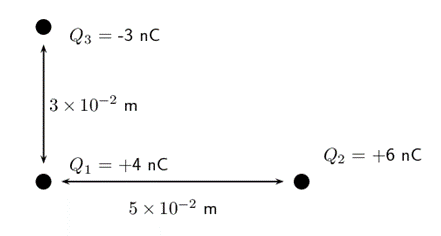
   Calculate the resultant electrostatic force on [latex]\scriptsize {{Q}_{1}}[/latex].
7. The magnitude of the force between two unknown charges is [latex]\scriptsize 8\text{ N}[/latex]. The distance between the charges is then halved. What is the new force between these charges? Explain your answer.
8. The force between two charged objects is [latex]\scriptsize F[/latex]. Which of the following changes will increase the force between the charges to [latex]\scriptsize 4F[/latex]? (Just write YES or NO)
   1. Double the charge on one of the objects.
   2. Increase the charge on one of the objects by a factor of [latex]\scriptsize 4[/latex].
   3. Double the charge on both objects.
   4. Increase the charge on both objects by a factor of [latex]\scriptsize 4[/latex].
   5. Halve the distance between the charges.
   6. Double the distance between the charges.
   7. Reduce the distance between the charges by a factor of [latex]\scriptsize 4[/latex].
   8. Increase the distance between the charges by a factor of [latex]\scriptsize 4[/latex].

The full solutions are at the end of the unit.

Unit 1: Solutions

Unit 1: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{ 2 x 1}{{\text{0}}^{{-5}}}\text{ C}\\{{\text{Q}}_{2}}&=6\text{ x 1}{{\text{0}}^{{-5}}}\text{ C}\\r&=\text{0}\text{.3 mm = 0}\text{.0003 m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(2\text{ x 1}{{\text{0}}^{{-5}}})(6\text{ x 1}{{\text{0}}^{{-5}}})}}{{{{{0.0003}}^{2}}}}\text{ = 1}\text{.2 x 1}{{\text{0}}^{8}}\end{align*}[/latex]
      Unlike charges, therefore force will be attraction.
      The force on [latex]\scriptsize {{Q}_{1}}[/latex] will be [latex]\scriptsize \text{1}\text{.2 x 1}{{\text{0}}^{8}}\text{ N}[/latex] downwards.
   2. The force on [latex]\scriptsize {{Q}_{2}}[/latex] will be [latex]\scriptsize \text{1}\text{.2 x 1}{{\text{0}}^{8}}\text{ N}[/latex] upwards.
2. .
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{ 6 x 1}{{\text{0}}^{{-5}}}\text{ C}\\{{\text{Q}}_{2}}&=1\text{ x 1}{{\text{0}}^{{-5}}}\text{ C}\\r&=\text{3 cm = 0}\text{.03 m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(6\text{ x 1}{{\text{0}}^{{-5}}})(1\text{ x 1}{{\text{0}}^{{-5}}})}}{{{{{0.03}}^{2}}}}\text{ = 6 000}\end{align*}[/latex]
   Unlike charges, therefore force is attraction. Force on [latex]\scriptsize {{Q}_{1}}[/latex] will be [latex]\scriptsize 6\text{ 000 N}[/latex] to the right.
3. .
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{3 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{\text{Q}}_{2}}&=5\text{ x 1}{{\text{0}}^{{-9}}}\text{ C}\\r&=\text{2 mm = 0}\text{.002 m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(3\text{ x 1}{{\text{0}}^{{-9}}})(5\text{ x 1}{{\text{0}}^{{-9}}})}}{{{{{0.002}}^{2}}}}\text{ = 0}\text{.034 N}\end{align*}[/latex]
   Like charges, therefore force will be repulsion.
4. .
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{ 4 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{\text{Q}}_{2}}&=3\text{ x 1}{{\text{0}}^{{-9}}}\text{ C}\\F&=\text{0}\text{.005 N}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\\0.005&=\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(4\text{ x 1}{{\text{0}}^{{-9}}})(3\text{ x 1}{{\text{0}}^{{-9}}})}}{{{{r}^{2}}}}\\r&=\text{ 4}\text{.65 x 1}{{\text{0}}^{{-3}}}\text{ m}\end{align*}[/latex]
   (Do not forget to square root to find [latex]\scriptsize r[/latex].)
5. First calculate force of [latex]\scriptsize {{Q}_{2}}[/latex] on [latex]\scriptsize {{Q}_{1}}[/latex]:
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{2 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{\text{Q}}_{2}}&=\text{1 x 1}{{\text{0}}^{{-9}}}\text{ }{{\text{C}}^{{}}}\\r&=\text{2 x 1}{{\text{0}}^{{-2}}}\text{ m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(2\text{ x 1}{{\text{0}}^{{-9}}})(1\text{ x 1}{{\text{0}}^{{-9}}})}}{{{{{(2\text{ x 1}{{\text{0}}^{{-2}}})}}^{2}}}}\text{ = 4}\text{.5 x 1}{{\text{0}}^{{-5}}}\end{align*}[/latex]
   These are like charges so they will repel. The force on [latex]\scriptsize {{Q}_{2}}[/latex] will be [latex]\scriptsize 4.5\text{ x 1}{{\text{0}}^{{-5}}}\text{ N }[/latex] to the right.
   Now calculate the force of [latex]\scriptsize {{Q}_{3}}[/latex] on [latex]\scriptsize {{Q}_{2}}[/latex]:
   [latex]\scriptsize \begin{align*}{{Q}_{3}}&=\text{3 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{Q}_{2}}&=\text{1 x 1}{{\text{0}}^{{-9}}}\text{ }{{\text{C}}^{{}}}\\r&=\text{4 x 1}{{\text{0}}^{{-2}}}\text{ m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{3}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(3\text{ x 1}{{\text{0}}^{{-9}}})(1\text{ x 1}{{\text{0}}^{{-9}}})}}{{{{{(4\text{ x 1}{{\text{0}}^{{-2}}})}}^{2}}}}\text{ = 1}\text{.69 x 1}{{\text{0}}^{{-5}}}\end{align*}[/latex]
   These are unlike charges so they will attract. The force on [latex]\scriptsize {{Q}_{2}}[/latex] will be [latex]\scriptsize 1.69\text{ x 1}{{\text{0}}^{{-5}}}\text{ N }[/latex] to the right.
   [latex]\scriptsize {{F}_{{net}}}=\text{ }{{F}_{1}}\text{ + }{{F}_{2}}[/latex] Let to the right be +ve
   
   .
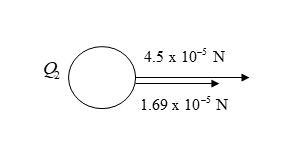
   [latex]\scriptsize =\text{ (4}\text{.5 x 1}{{\text{0}}^{{-5}}})+\text{ (1}\text{.69 x 1}{{\text{0}}^{{-5}}})=6.19\text{ x 1}{{\text{0}}^{{-5}}}\text{ N}[/latex] to the right
6. First calculate force of [latex]\scriptsize {{Q}_{2}}[/latex] on [latex]\scriptsize {{Q}_{1}}[/latex]:
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{ 4 nC = 4 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{Q}_{2}}&=6\text{ nC = }6\text{ x 1}{{\text{0}}^{{-9}}}\text{ }{{\text{C}}^{{}}}\\r&=\text{5 x 1}{{\text{0}}^{{-2}}}\text{ m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(4\text{ x 1}{{\text{0}}^{{-9}}})(6\text{ x 10}9)}}{{{{{(5\text{ x 1}{{\text{0}}^{{-2}}})}}^{2}}}}\text{ = 8}\text{.64 x 1}{{\text{0}}^{{-5}}}\end{align*}[/latex]
   These are like charges, so they repel. The force on [latex]\scriptsize {{Q}_{1}}[/latex] will be [latex]\scriptsize 8.64\text{ x1}{{\text{0}}^{{-5}}}\text{ N }[/latex] to the left.
   Now calculate force of [latex]\scriptsize {{Q}_{3}}[/latex] on [latex]\scriptsize {{Q}_{2}}[/latex]:
   [latex]\scriptsize \begin{align*}{{Q}_{1}}&=\text{ 4 nC = 4 x 1}{{\text{0}}^{{-9}}}\text{ C}\\{{Q}_{3}}&=3\text{ nC = 3 x 1}{{\text{0}}^{{-9}}}\text{ }{{\text{C}}^{{}}}\\r&=\text{3 x 1}{{\text{0}}^{{-2}}}\text{ m}\\F&=\text{ }\displaystyle \frac{{k{{Q}_{1}}{{Q}_{2}}}}{{{{r}^{2}}}}\text{ = }\displaystyle \frac{{(9\text{ x 1}{{\text{0}}^{9}})(4\text{ x 1}{{\text{0}}^{{-9}}})(3\text{ x 1}{{\text{0}}^{{-9}}})}}{{{{{(3\text{ x 1}{{\text{0}}^{{-2}}})}}^{2}}}}\text{ = 1}\text{.2 x 1}{{\text{0}}^{{-4}}}\end{align*}[/latex]
   These are unlike charges so they will attract. The force on [latex]\scriptsize {{Q}_{1}}[/latex] will be [latex]\scriptsize \text{1}\text{.2 x1}{{\text{0}}^{{-4}}}\text{ N }[/latex]upwards.
   Now find the resultant of these two forces:
   
   .
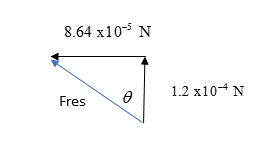
   [latex]\scriptsize \begin{align*}{{({{F}_{{ne{{t}^{{}}}}}})}^{2}}&=\text{ (8}\text{.64 x 1}{{\text{0}}^{{-5}}}{{)}^{2}}+\text{ (1}\text{.2 x 1}{{\text{0}}^{{-4}}}{{)}^{2}}\\{{F}_{{net}}}&=\text{ 1}\text{.48 x 1}{{\text{0}}^{{-4}}}\text{ N}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\tan \theta &=\text{ }\displaystyle \frac{{8.64\text{ x1}{{\text{0}}^{{-5}}}}}{{1.2\text{ x 1}{{\text{0}}^{{-4}}}}}\\\theta &=\text{35}\text{.7}{{\text{5}}^{o}}\end{align*}[/latex]
   Resultant force on [latex]\scriptsize {{Q}_{1}}[/latex] is [latex]\scriptsize \text{1}\text{.48 x 1}{{\text{0}}^{{-4}}}\text{ N}[/latex] at [latex]\scriptsize \text{35}\text{.7}{{\text{5}}^{o}}[/latex] from the vertical.
7. From Coulomb’s law, the magnitude of the force between two charges is inversely proportional to the square of the distance between the charges. You write this mathematically as: [latex]\scriptsize F\propto \text{ }\displaystyle \frac{1}{{{{r}^{2}}}}[/latex].
   If the distance between the charges is halved, this means that the new force ([latex]\scriptsize {{F}_{2}}[/latex]) is related to the old force [latex]\scriptsize F[/latex] in this way:
   [latex]\scriptsize {{F}_{2}}\propto \text{ }\displaystyle \frac{1}{{{{{(\displaystyle \frac{1}{2})}}^{2}}}}\text{ }     F\text{ }\propto \text{ }\displaystyle \frac{1}{{\displaystyle \frac{1}{4}}}\text{ = 4}F[/latex]
   .
   So the new force will be greater than the previous force [latex]\scriptsize F[/latex] by a factor of [latex]\scriptsize 4[/latex]. Therefore the magnitude of the force will be [latex]\scriptsize 8\text{ x 4 = 32 N}[/latex].
8. .
   1. Double the charge on one of the objects. NO
      ([latex]\scriptsize F\text{ }\propto \text{ }Q[/latex], force is proportional to charge, so this will increase the force to [latex]\scriptsize 2F[/latex], not [latex]\scriptsize 4F[/latex].)
   2. Increase the charge on one of the objects by a factor of [latex]\scriptsize 4[/latex]. YES
      ([latex]\scriptsize F\text{ }\propto \text{ }Q[/latex], force is proportional to charge, so this will increase the force to [latex]\scriptsize 4F[/latex].)
   3. Double the charge on both objects. YES
      ([latex]\scriptsize F\text{ }\propto \text{ }Q[/latex], force is proportional to charge, so this will increase the force to [latex]\scriptsize 4F[/latex].)
   4. Increase the charge on both of the objects by a factor of 4. NO
      ([latex]\scriptsize F\text{ }\propto \text{ }Q[/latex], force is proportional to charge, so this will increase the force to [latex]\scriptsize 16F[/latex], not [latex]\scriptsize 4F[/latex].)
   5. Halve the distance between the charges. YES
      ([latex]\scriptsize F\text{ }\propto \text{ }\displaystyle \frac{1}{{{{r}^{2}}}}[/latex], force is inversely proportional to the square of the distance between the charges, so this will increase the force to [latex]\scriptsize 4F[/latex].)
   6. Double the distance between the charges. NO
      ([latex]\scriptsize F\text{ }\propto \text{ }\displaystyle \frac{1}{{{{r}^{2}}}}[/latex], force is inversely proportional to the square of the distance between the charges, so this will decrease the force to [latex]\scriptsize \displaystyle \frac{1}{4}F[/latex].)
   7. Reduce the distance between the charges by a factor of [latex]\scriptsize 4[/latex]. NO
      ([latex]\scriptsize F\text{ }\propto \text{ }\displaystyle \frac{1}{{{{r}^{2}}}}[/latex], force is inversely proportional to the square of the distance between the charges, so this will increase the force to [latex]\scriptsize 16F[/latex].)
   8. Increase the distance between the charges by a factor of [latex]\scriptsize 4[/latex]. NO
      ([latex]\scriptsize F\text{ }\propto \text{ }\displaystyle \frac{1}{{{{r}^{2}}}}[/latex], force is inversely proportional to the square of the distance between the charges, so this will decrease the force to [latex]\scriptsize \displaystyle \frac{1}{{16}}F[/latex].)

Back to Unit 1: Assessment