Waves, sound and light: Describe, analyse and apply principles of longitudinal waves in everyday life
Unit 3: Resonance
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Identify and describe resonance in musical instruments and structures (building and bridges).
What you should know
Before you start this unit, make sure you can:
- Describe and calculate:
- wave speed
- wavelength
- frequency
- amplitude.
- Distinguish between standing and moving waves.
- Identify and describe superposition in standing waves.
Introduction
In level 2 subject outcome 3.1 unit 4 we learnt about standing waves and resonance and the importance of these concepts in acoustics, architecture and the large structures such as buildings and bridges.
In this unit, we are going to dive a little deeper into these topics and their real-world applications. We will see how these concepts explain why different instruments, playing the same note, still sound different; why some bridges sway badly in the wind; and why modern skyscrapers are far more stable than they might appear even in high winds or during earthquakes.
Resonance revision: Interference and standing waves
From level 2 subject outcome 3.1 unit 4 we know that a standing wave is a perceived wave pattern that results from the interaction of two travelling waves moving in opposite directions in a medium (like a guitar string or a column of air). A standing wave is so called because it appears to stand still.
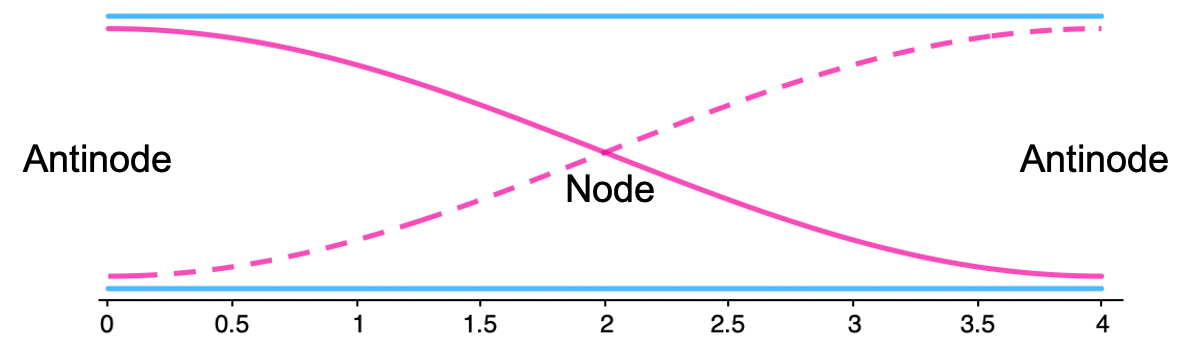
Remember, the interaction of two or more waves in the same location is called superposition. When the amplitudes of superimposed waves combine, constructive interference occurs. This happens when two positive or two negative disturbances combine, resulting in a bigger amplitude than either of the two individual amplitudes (see figure 1).

Destructive interferences occurs when a positive and a negative disturbance combine, resulting in a smaller amplitude than that of the bigger of the two original amplitudes (see figure 2).
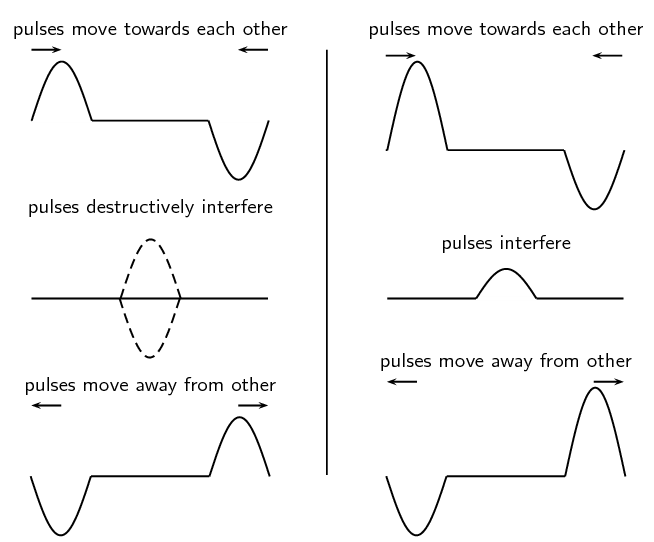
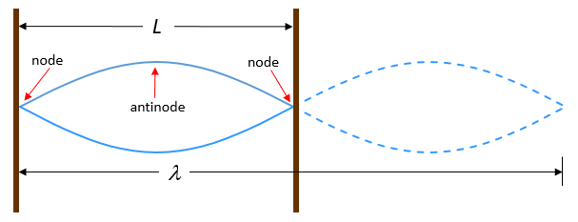
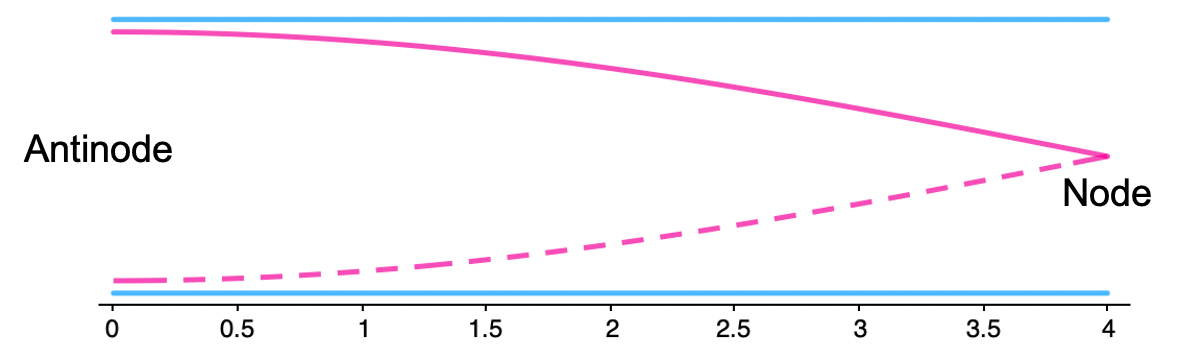
A point of perfect destructive interference in a standing wave is called a node. A node represents a point of zero amplitude on a standing wave. A point of perfect constructive interference in a standing wave is called an antinode. An antinode represents a point of maximum amplitude on a standing wave (see figure 3).
Note
If you have an internet connection, have a look at a standing wave on a string simulation.
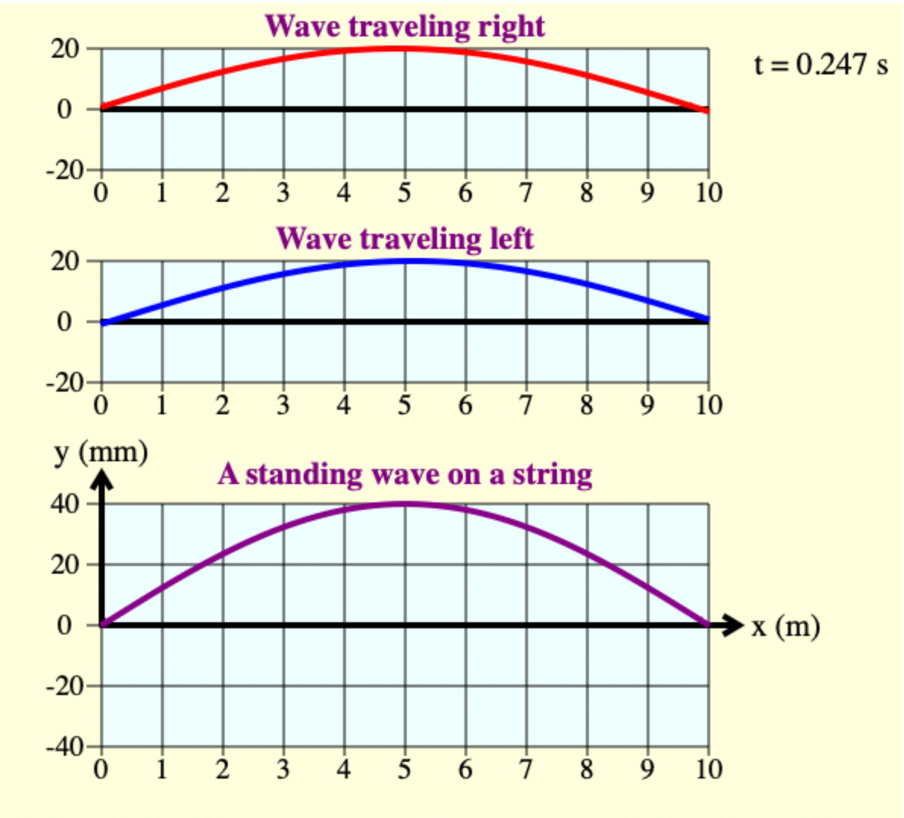
This is an example of a standing wave produced on a string as the waves moving in opposite directions along the string interfere constructively and destructively creating nodes and antinodes.
Figure 4 shows an image taken from the standing wave simulation. It is important to note that, because of the constructive interference at the antinode, the amplitude of the standing wave is twice as great as the amplitude of either of the individual waves. When standing waves are produced, the energy of the whole system is increased.
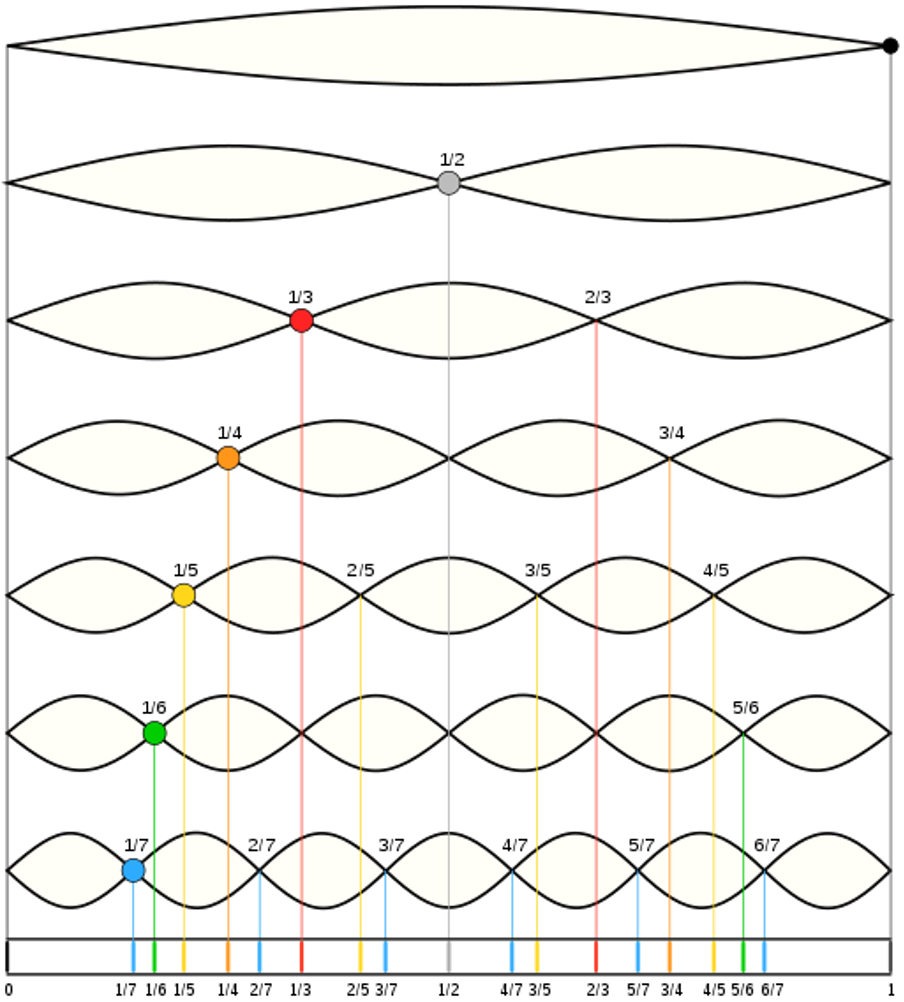
Now you can see that a standing wave forming on a string of a certain length depends entirely on the wavelength of the wave traveling along that string (and hence its frequency). If the wavelength is too short or too long (or the frequency is too high or too low), the interference of the waves travelling in opposite directions along the string will not be such as to let the peaks and troughs line up just right to create a standing wave.
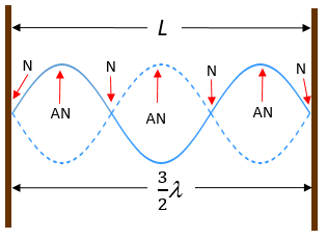
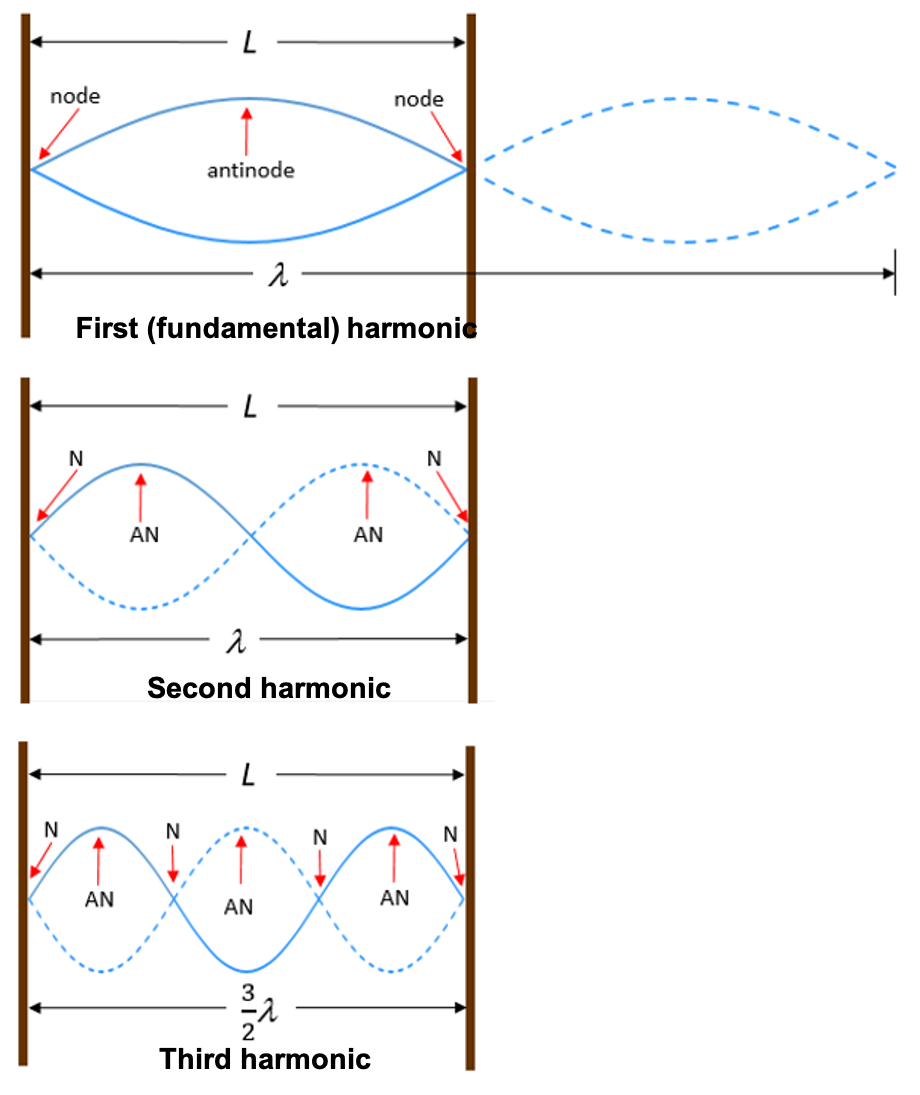
In figure 3, you can see that a standing wave will form if the wavelength of the wave is exactly double the length of the string. In figure 5 and figure 6 you can see that a standing wave will also form if the wavelength of the wave is exactly the same as the length of the string (figure 5) or exactly two-thirds the length of the string (figure 6).
The standing wave equation
In level 2 subject outcome 3.1 unit 4, we discovered that the relationship between the length of the string and the wavelength of waves that result in standing waves is [latex]\scriptsize \displaystyle L=\displaystyle \frac{{n{{\lambda }_{n}}}}{2}[/latex], where [latex]\scriptsize \displaystyle L[/latex] is the length of the string, [latex]\scriptsize \displaystyle n[/latex] is any natural number and [latex]\scriptsize \displaystyle {{\lambda }_{n}}[/latex] is the wavelength of the wave creating the [latex]\scriptsize {{n}^{{th}}}[/latex] kind of standing wave.
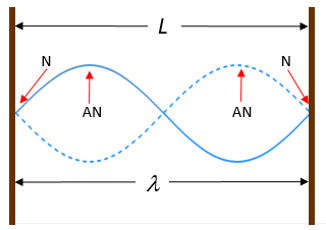
We call the different standing wave patterns . Figure 7 shows the first or fundamental harmonic, the second harmonic, and the third harmonic.
We can rewrite the equation in terms of the wavelength of the wave that results in a harmonic standing wave pattern as [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex].
Note
Go back to the standing wave simulation and click the ‘n=2’, ‘n=3’, ‘n=4’, ‘n=5’ and ‘n=6’ buttons at the bottom to see what the second, third, fourth, fifth and sixth harmonics look like. Notice how the frequency of the first harmonic wave is lower than the frequency of the fifth harmonic, but that the wavelength of the first harmonic standing wave is bigger.
An object vibrating at one (or more) of its harmonics is said to be resonating. This phenomenon is called resonance. Every material has a natural frequency at which it will vibrate, called its resonant frequency. When a material resonates, its natural vibration is amplified because of the standing wave patterns created through constructive interference, which increases the amplitude of the waves travelling through the object (the medium).
This is what happens when you pluck a guitar string. The string naturally vibrates at one or more of its resonant frequencies (those frequencies that result from waves of just the right wavelength to cause standing wave patterns to form on the string). As you shorten the sting by placing your finger at various positions on the fretboard (see figure 8), you change the length of the string, hence the wavelength of the waves that result in resonance and hence the frequency of these waves. In other words, you change the pitch of the sound produced.

Now, think of a bridge across a river. A bridge is similar to a guitar string fixed at both ends. If a wind blows or there is an earthquake that causes the bridge to vibrate at just the right frequency (its resonant frequency), a standing wave will appear across the bridge amplifying the inputs that got the bridge vibrating in the first place. As the amplitude increases, the energy of the wave increases until the bridge can no longer handle the forces, and so collapses. This is partly what happened to the Tacoma bridge in 1940.
Did you know?
The famous Tacoma Bridge collapse was not purely the result of wind causing the bridge to vibrate at its resonant frequency. Vortices of wind catching the bridge from the side and causing it to sway back and forth were actually the more immediate cause of its failure.
Note
The same phenomenon explains why certain frequencies of sound can cause wine glasses to shatter. If you have an internet connection, watch the video called “How I broke a wine glass with my VOICE (using science!)” to see the principle of resonance and resonant frequency in action and hear a really good explanation for what is going on.
Note
Before moving on, if you have an internet connection, watch the video called “Standing waves on strings” for a more detailed explanation of what we have covered so far.
Resonance in tubes
We saw in the section on standing waves in strings that a resonant system, like a guitar string, always has nodes on both ends because the string is fixed at both ends. By definition, if it is fixed at these points, it cannot vibrate at these points.
But systems like those created by guitar strings are not the only kinds of systems that can experience resonance. Two other types of systems can experience resonance. These are tubes that are open at both ends and tubes that are open at one end. A flute is an example of a tube open at both ends (an open tube). A clarinet or an empty bottle is an example of a tube open at only one end (a closed tube).
Resonance in open tubes
Open-tube systems, as we will see, can be thought of as the ‘inverse’ of string systems. Like string systems, waves with particular wavelengths (relative to the length of the tube or column of air) will cause standing wave patterns to occur inside the column of air and, hence, resonance.
Activity 3.1: Investigate resonance in open tubes
Time required: 20 minutes
What you need:
- an internet connection
- a pen or pencil
- a blank piece of paper
What to do:
- Open the ‘Harmonics of open pipe’ simulation.
.
Here you will find an open tube system with two sliders – one for the harmonic number and another for the length of the tube. With Harmonic = 1, identify the location of and count the number of nodes and antinodes. - Change the number of the harmonic to 2, 3, 4, 5 and 6, each time locating and counting the number of nodes and antinodes. Are nodes or antinodes always created at the ends of the tube? How does this compare to the string system?
- Now create a table like the one below to record the wavelength of the resulting standing waves for each harmonic as well as the number of nodes.
Harmonic Number of nodes Wavelength of standing wave 1 2 3 4 5 6 - Using the data, determine an equation that relates the wavelength of the standing wave for each harmonic to the length of the tube for each harmonic. Change the length of the open tube to [latex]\scriptsize 2\ \text{m}[/latex] to make sure your equation is correct. How does this equation relate to the one for the standing wave wavelength equation for a string?
- Set the harmonic to 1. What is the frequency of the standing wave when the open tube is [latex]\scriptsize 4\ \text{m}[/latex] long? What is its frequency when the tube is [latex]\scriptsize 3\ \text{m}[/latex] long? If this were a musical instrument, what change would you hear when you changed the length of the open tube from [latex]\scriptsize 4\ \text{m}[/latex] to [latex]\scriptsize 3\ \text{m}[/latex]?
- Look back at the standing wave on a string simulation or figures 3, 5 and 6 and describe the difference between the pattern of nodes and antinodes of the different harmonics on a string and in an open tube.
What did you find?
- The first harmonic is a standing wave pattern with two antinodes and one node. The antinodes are at each end of the tube and the node is in the centre.
.
- The following table shows a summary of the second to sixth harmonics.
Harmonic Number of nodes Number of antinodes Nodes and antinodes 2 2 3 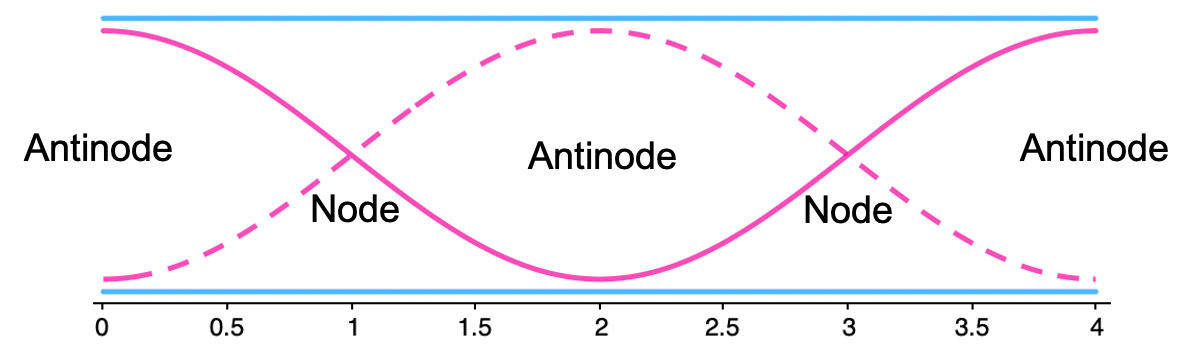
3 3 4 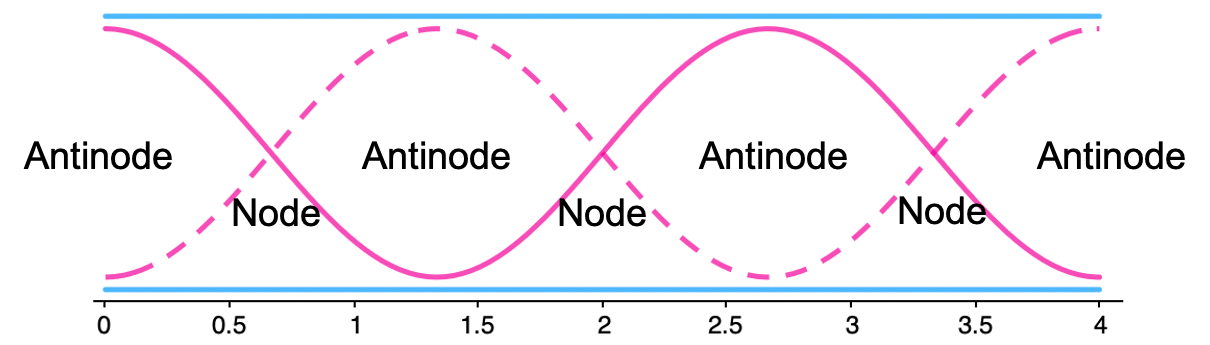
4 4 5 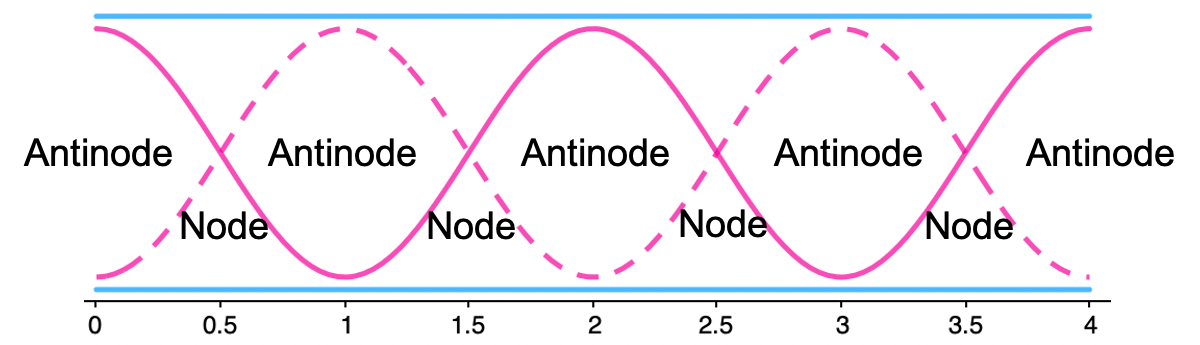
5 5 6 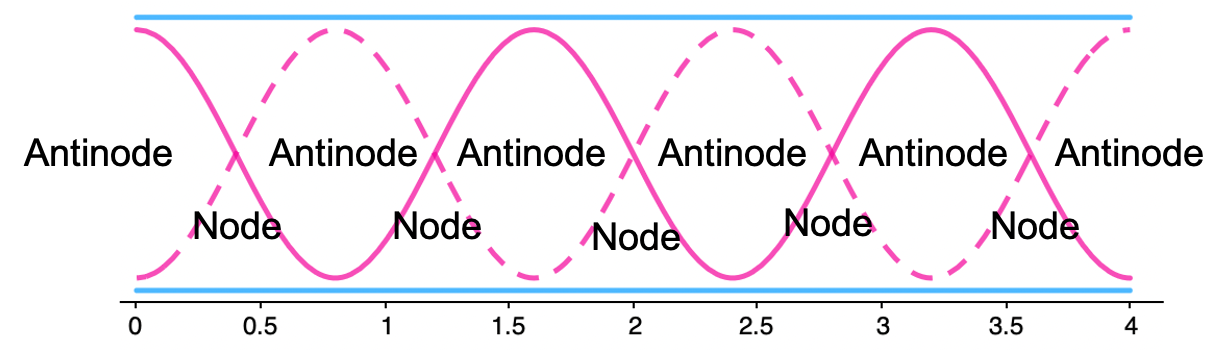
6 6 7 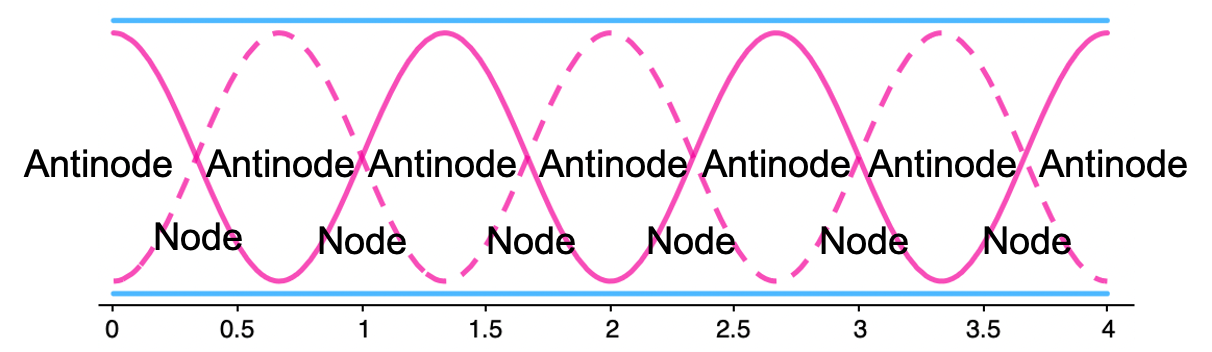
Antinodes are always created at the ends of the tube. This is the opposite of string systems, where nodes are always created at the ends.
- The table below shows the wavelengths of the resulting standing waves for each harmonic and the corresponding number of nodes present.
Harmonic Number of nodes Wavelength of standing wave 1 1 [latex]\scriptsize 8\ \text{m}[/latex] 2 2 [latex]\scriptsize 4\ \text{m}[/latex] 3 3 [latex]\scriptsize 2.67\ \text{m}[/latex] 4 4 [latex]\scriptsize 2\ \text{m}[/latex] 5 5 [latex]\scriptsize 1.6\ \text{m}[/latex] 6 6 [latex]\scriptsize 1.33\ \text{m}[/latex] - The equation relating the wavelength of the standing wave for the different harmonics for an open tube of length [latex]\scriptsize L[/latex] is [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex]where [latex]\scriptsize n[/latex] is the harmonic number. This is the same equation as that for a string.
- The frequency of the first harmonic for a tube [latex]\scriptsize L=4\ \text{m}[/latex] is [latex]\scriptsize 42.5\ \text{Hz}[/latex]. The frequency of the first harmonic for a tube [latex]\scriptsize L=3\ \text{m}[/latex] is [latex]\scriptsize 56.67\ \text{Hz}[/latex]. Because the frequency of the first harmonic for the [latex]\scriptsize 3\ \text{m}[/latex] tube is higher than for the [latex]\scriptsize 4\ \text{m}[/latex] tube, a note with a higher pitch would be heard.
- Remember, the standing wave pattern of nodes and antinodes for an open tube is the exact inverse of that for a string. Where there are nodes on the string, there are antinodes in the open tube and vice versa.
We have seen from activity 3.1 that the resonance and harmonics of an open tube are very similar to those of a string. Where a string is fixed at both ends, an open tube is open at both ends. The pattern of nodes and antinodes for each harmonic on a string is the inverse of that in an open tube. However, the equation relating the wavelength of the standing wave to the harmonic number in each system is exactly the same.
Sometimes people refer to the harmonics of a system as overtones. In simple terms, the first overtone is the second harmonic, the third overtone is the fourth harmonic, and so on.
Take note!
[latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex] for [latex]\scriptsize n=1,2,3,\ldots[/latex] relates the wavelength of the standing waves in an open tube to the length of the tube.
This is the same equation that relates the wavelengths of the standing waves on a string to the length of the string.
Example 3.1
Find the length of an open tube that has a fundamental frequency of [latex]\scriptsize 128\ \text{Hz}[/latex]. What is the frequency of the fifth harmonic? Assume that the speed of sound in air is [latex]\scriptsize 344\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex].
Solution
We know that the length of an open tube is related to the wavelength of the harmonics (the wavelengths of the different resonant frequencies) by [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex]. If we are interested in the fundamental frequency, we are interested in the first harmonic. In other words, [latex]\scriptsize n=1[/latex].
But first, we need to determine what the wavelength of the wave with a frequency of [latex]\scriptsize 128\ \text{Hz}[/latex] is.
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}=\displaystyle \frac{{344\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{128\ \text{Hz}}}=2.69\ \text{m}\end{align*}[/latex]
[latex]\scriptsize n=1[/latex]
[latex]\scriptsize \lambda =2.69\ \text{m}[/latex]
[latex]\scriptsize \begin{align*}{{\lambda }_{1}} & =\displaystyle \frac{{2L}}{1}\\\therefore L & ={{\lambda }_{1}}\times \displaystyle \frac{1}{2}=2.69\ \text{m}\times \displaystyle \frac{1}{2}=1.34\ \text{m}\end{align*}[/latex]
The length of the tube would need to be [latex]\scriptsize 1.34\ \text{m}[/latex].
To work out the frequency of the fifth harmonic, we need to let [latex]\scriptsize n=5[/latex] for a tube of length [latex]\scriptsize L=1.34\ \text{m}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}{{\lambda }_{5}} &=\displaystyle \frac{{2L}}{5}\\ & =\displaystyle \frac{{2\times 1.34\ \text{m}}}{5}=0.54\ \text{m}\end{align*}[/latex]
We have the wavelength of the fifth harmonic. Now we can calculate its frequency.
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }=\displaystyle \frac{{344\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{0.54\ \text{m}}}=637.04\ \text{Hz}\end{align*}[/latex]
Note
If you have an internet connection watch the video called Standing waves in open tubes for another explanation.
Resonance in closed tubes
Closed-tube systems are those which are closed at one end only. Like string systems and open tubes, waves with particular wavelengths (relative to the length of the tube or column of air) will cause standing wave patterns to occur inside the column of air contained inside a closed tube and, hence, resonance.
Because a standing wave in a closed tube has a node at the closed end and an antinode at the open end, standing waves occur only at the odd harmonics (i.e. 1, 3, 5, 7, etc.).
Note
If you have an internet connection, watch Standing waves in closed tubes for an explanation as to why.
Activity 3.2: Investigate resonance in closed tubes
Time required: 20 minutes
What you need:
- an Internet connection
- a pen or pencil
- a blank piece of paper
What to do:
- Open the ‘Harmonics of closed pipe’ simulation.
.
Here you will find a closed-tube system with two sliders – one for the number of nodes and another for the length of the tube. - With Number of nodes = 1, identify the location of and count the number of nodes and antinodes.
- Change the number of nodes to 2, 3, 4, 5 and 6, each time locating and counting the number of nodes and antinodes. These correspond to harmonics 3, 5, 7, 9 and 11.
- Now create a table like the one below to record the wavelength of the resulting standing waves for each harmonic as well as the number of nodes.
Harmonic Number of nodes Wavelength of standing wave 1 3 5 7 9 11 - Using the data, determine an equation that relates the wavelength of the standing wave for each harmonic to the length of the tube for each harmonic. Change the length of the open tube to [latex]\scriptsize 2\ \text{m}[/latex] to make sure your equation is correct. How does this equation relate to the one for the standing wave wavelength equation for a string?
- Set the number of nodes to 1. What is the frequency of the standing wave when the closed tube is [latex]\scriptsize 4\ \text{m}[/latex] long? What is its frequency when the tube is [latex]\scriptsize 3\ \text{m}[/latex] long? If this were a musical instrument, what change would you hear when you changed the length of the open tube from [latex]\scriptsize 4\ \text{m}[/latex] to [latex]\scriptsize 3\ \text{m}[/latex]?
What did you find?
- The first harmonic is a standing wave pattern with one antinode and one node.
.
- The table below shows a summary of the second to sixth harmonics.
Harmonic Number of nodes Wavelength of standing wave 3 2 2 5 3 3 7 4 4 9 5 5 11 6 6 - The table below shows the wavelengths of the resulting standing waves for each harmonic and the corresponding number of nodes present.
Harmonic Number of nodes Wavelength of standing wave 1 1 [latex]\scriptsize 16\ \text{m}[/latex] 3 2 [latex]\scriptsize 5.33\ \text{m}[/latex] 5 3 [latex]\scriptsize 3.2\ \text{m}[/latex] 7 4 [latex]\scriptsize 2.29\ \text{m}[/latex] 9 5 [latex]\scriptsize 1.78\ \text{m}[/latex] 11 6 [latex]\scriptsize 1.45\ \text{m}[/latex] - The equation relating the wavelength of the standing wave for the different harmonics for an open tube of length [latex]\scriptsize L[/latex]is [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{4L}}{n}[/latex]where [latex]\scriptsize n[/latex] is the harmonic number. This is the same equation as that for a string.
- The frequency of the first harmonic for a tube [latex]\scriptsize L=4\ \text{m}[/latex] is [latex]\scriptsize 21.25\ \text{Hz}[/latex]. The frequency for the first harmonic for a tube [latex]\scriptsize L=3\ \text{m}[/latex] is [latex]\scriptsize 56.67\ \text{Hz}[/latex]. Because the frequency of the first harmonic for the [latex]\scriptsize 3\ \text{m}[/latex] tube is higher than for the [latex]\scriptsize 4\ \text{m}[/latex] tube, a note with a higher pitch would be heard.
Activity 3.2 showed us three important things:
- Closed tubes can also experience resonance and have different wavelengths of waves that cause standing waves.
- Closed tubes have only odd harmonics.
- The equation relating the wavelength of the standing wave to the length of the tube is [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{4L}}{n}[/latex] for [latex]\scriptsize n=1,3,5,\ldots[/latex], which is different from that of open tubes and strings ([latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex] for [latex]\scriptsize n=1,2,3,\ldots[/latex]).
Take note!
[latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{4L}}{n}[/latex] for [latex]\scriptsize n=1,3,5,\ldots[/latex] relates the wavelength of the standing waves in a closed tube to the length of the tube. Remember only odd harmonics are allowed.
Example 3.2
A closed tube has a length of [latex]\scriptsize 32\ \text{cm}[/latex]. What is the frequency of the fifth harmonic? Assume that the speed of sound in air is [latex]\scriptsize 344\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex].
Solution
In order to find the frequency of the fifth harmonic, we need to find its wavelength. We have an equation that relates the wavelength of the harmonics with the length of a closed tube. This is [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{4L}}{n}[/latex] for [latex]\scriptsize n=1,3,5,\ldots[/latex]. In our case [latex]\scriptsize n=5[/latex] and [latex]\scriptsize L=0.32\ \text{m}[/latex].
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{4L}}{n}\\\therefore {{\lambda }_{5}} & =\displaystyle \frac{{4\times 0.32\ \text{m}}}{5}=0.256\ \text{m}=25.6\ \text{cm}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }=\displaystyle \frac{344\ \text{m.s}^{-1}}{0.256\ \text{m}}=1\ 343.75\ \text{Hz}\end{align*}[/latex]
Resonance in real life
Resonance and harmonics are a big part of the reason that different instruments sound different. The A string of a bass produces a sound with a frequency of [latex]\scriptsize 110\ \text{Hz}[/latex]. This is the first or fundamental harmonic. However, it also produces sound waves of frequencies related to all of the other possible harmonics.
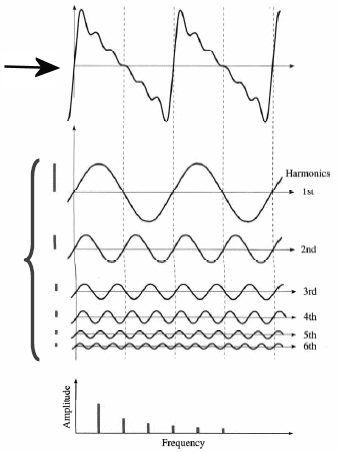
The second harmonic, for example, has a wavelength half the fundamental or first harmonic (see figure 9). Therefore, it has a frequency double the first harmonic of [latex]\scriptsize 220\ \text{Hz}[/latex]. Remember that the speed of the wave does not change and that [latex]\scriptsize v=f\times \lambda[/latex]. The second harmonic is said to be one octave higher than the first harmonic. The third harmonic is higher still but not another whole octave. Its wavelength is one third the first harmonic’s (see figure 9).
It is the combination and interaction of these different harmonics that give a guitar its distinctive sound. The same note, played on a cello will also be dominated by the same first harmonic at [latex]\scriptsize 110\ \text{Hz}[/latex], but a different combination of other harmonics with be produced and will interact to give the cello its own unique sound. Figure 10 illustrates how the combination of the different harmonics combine to produce a unique waveform for an instrument.
A guitar player produces notes of different frequencies (pitches) by changing the length of each string. The shorter the string, the higher the fundamental frequency or first harmonic that is produced and so the higher the note.
Wind instruments such as flutes (open tubes) and clarinets (closed tubes) have keys that open and close the tube at different places. By manipulating these keys, the musician can change the length of the open or closed tube created inside the instrument. Once again, the shorter the tube, the higher the note that is produced.
An understanding of resonance and the frequency of standing waves is also used when building skyscrapers. Skyscrapers, being fixed to the ground but not to the sky, behave like closed tubes. If an earthquake or wind causes the building to start vibrating at any of its resonant frequencies, this energy will get amplified and might cause the building to collapse.
To stop this happening, engineers use . As the building starts to sway, big heavy masses (usually near the top of the building) start to move like a pendulum. But these systems are designed to have resonant frequencies very similar to the building’s. The result of this is that they remove energy from the building and, therefore, keep it from swaying too much.
Note
If you have an internet connection, watch the video called What is a Tuned Mass Damper? for an explanation of how these systems work.
Exercise 3.1
- Why is the lowest note that can be played on a clarinet (a closed tube) lower note than what can be played on a flute (open tube) when both instruments are about the same length?
- What length should a tube open at both ends have to produce a fundamental frequency of [latex]\scriptsize 110\ \text{Hz}[/latex] on a day when the speed of sound is [latex]\scriptsize 340\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]?
- What are the first three overtones of a bassoon that has a fundamental frequency of [latex]\scriptsize 90\ \text{Hz}[/latex]? It is open at both ends.
- How long must a flute (an open tube) be in order to play middle C, which has a fundamental frequency of [latex]\scriptsize 262\ \text{Hz}[/latex], on a day when the speed of sound in air is [latex]\scriptsize 340\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]?
The full solutions can be found at the end of the unit.
Summary
In this unit you have learnt the following:
- Sound waves (longitudinal waves) interfere in the same way as transverse waves.
- Sound waves (longitudinal waves) show the same resonance patterns and properties as transverse waves.
- In air columns, the lowest resonant frequency is called the fundamental, whereas all higher resonant frequencies are called overtones. Collectively, they are called harmonics.
- The resonant wavelengths of a tube closed at one end (a closed tube) are [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{4L}}{n}[/latex] where [latex]\scriptsize n=1,3,5,\ldots[/latex] .
- The resonant wavelengths of a tube open at both ends (an open tube) are [latex]\scriptsize {{\lambda }_{n}}=\displaystyle \frac{{2L}}{n}[/latex] where [latex]\scriptsize n=1,2,3,\ldots[/latex] .
Unit 3: Assessment
Suggested time to complete: 40 minutes
- Is the wavelength of the fundamental standing wave in a tube open at both ends greater than, equal to, or less than the wavelength of the fundamental standing wave in a tube of the same length with only one open end?
- What is the fundamental frequency of a [latex]\scriptsize 0.672\ \text{m}[/latex] long tube, open at both ends, on a day when the speed of sound is [latex]\scriptsize 344\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]? What is the frequency of its second harmonic?
- If a wind instrument, such as a tuba, plays a note with a fundamental frequency of [latex]\scriptsize 32\ \text{Hz}[/latex], what are the first three overtones? It is closed at one end.
- What tube length does an oboe need to produce the note [latex]\scriptsize G4[/latex] which has a fundamental frequency of [latex]\scriptsize 392\ \text{Hz}[/latex] on a day when the speed of sound is [latex]\scriptsize 343\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]? It is open at both ends.
- What is the length of a tube that has a fundamental frequency of [latex]\scriptsize \displaystyle 176\ \text{Hz}[/latex] and a first overtone of [latex]\scriptsize 352\ \text{Hz}[/latex] if the speed of sound is [latex]\scriptsize 342\ \text{m}\text{.}{{\text{s}}^{{-1}}}[/latex]?
The full solutions can be found at the end of the unit.
Unit 3: Solutions
Exercise 3.1
- Let the instruments play the lowest note possible (i.e. the note emitted when the tubes are made their longest). A flute is a tube with two open ends. Therefore, the wavelength of the fundamental standing wave ([latex]\scriptsize n=1[/latex]) is [latex]\scriptsize \lambda =2L[/latex]. A clarinet is open at one end and closed at the other end by the player’s lips and the reed. Therefore, the wavelength of the fundamental standing wave ([latex]\scriptsize n=1[/latex]) is [latex]\scriptsize \lambda =4L[/latex]. As the wavelength of the clarinet’s standing wave is longer, its frequency is lower.
- .
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}=\displaystyle \frac{340\ \text{m.s}^{-1}}{110\ \text{Hz}}=3.09\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L\\\therefore L & =\displaystyle \frac{{3.09\ \text{m}}}{2}=1.55\ \text{m}\end{align*}[/latex] - The first three overtones are the second, third and fourth harmonics of an open tube.
[latex]\scriptsize \displaystyle \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L\\{{\lambda }_{2}} & =\displaystyle \frac{{2L}}{2}=L\\{{\lambda }_{3}} & =\displaystyle \frac{{2L}}{3}=\displaystyle \frac{2}{3}L\\{{\lambda }_{4}} & =\displaystyle \frac{{2L}}{4}=\displaystyle \frac{1}{2}L\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }\\\therefore {{f}_{1}} & =\displaystyle \frac{v}{{2L}}=90\ \text{Hz}\\{{f}_{2}} & =2\times \left( {\displaystyle \frac{v}{{2L}}} \right)=2\times 90\ \text{Hz}=180\ \text{Hz}\\{{f}_{3}} & =3\times \left( {\displaystyle \frac{v}{{2L}}} \right)=3\times 90\ \text{Hz}=270\ \text{Hz}\\{{f}_{4}} & =4\times \left( {\displaystyle \frac{v}{{2L}}} \right)=4\times 90\ \text{Hz}=360\ \text{Hz}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}=\displaystyle \frac{340\ \text{m.s}^{-1}}{262\ \text{Hz}}=1.30\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L\\\therefore L & =\displaystyle \frac{{1.30\ \text{m}}}{2}=0.65\ \text{m}=65\ \text{cm}\end{align*}[/latex]
Unit 3: Assessment
- In a tube with two open ends [latex]\scriptsize {{\lambda }_{1}}=2L[/latex]. But [latex]\scriptsize v=f\times \lambda[/latex]. Therefore [latex]\scriptsize \displaystyle \frac{v}{f}=2L[/latex].
In a tube with only one open end [latex]\scriptsize {{\lambda }_{1}}=4L[/latex]. But [latex]\scriptsize v=f\times \lambda[/latex]. Therefore [latex]\scriptsize \displaystyle \frac{v}{f}=4L[/latex].
The wavelength of the fundamental standing wave in a tube open at both ends is less than the wavelength of the fundamental standing wave in a tube with only one open end. - .
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L=0.672\ \text{m}\times 2=1.344\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }=\displaystyle \frac{{340\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{1.344\ \text{m}}}=255.95\ \text{Hz}\end{align*}[/latex].
.
The fundamental frequency is [latex]\scriptsize 255.95\ \text{Hz}[/latex]. The second harmonic has a wavelength half the fundamental harmonic. Therefore, the second harmonic has a frequency double the fundamental frequency or [latex]\scriptsize 511.9\ \text{Hz}[/latex]. - The first three overtones are the third, fifth and seventh harmonics of a closed tube.
[latex]\scriptsize \displaystyle \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{4L}}{n}\\\therefore {{\lambda }_{1}} & =4L\\{{\lambda }_{3}} & =\displaystyle \frac{{4L}}{3}=\displaystyle \frac{4}{3}L\\{{\lambda }_{4}} & =\displaystyle \frac{{4L}}{5}=\displaystyle \frac{4}{5}L\\{{\lambda }_{7}} & =\displaystyle \frac{{4L}}{7}=\displaystyle \frac{4}{7}L\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }\\\therefore {{f}_{1}} & =\displaystyle \frac{v}{{4L}}=32\ \text{Hz}\\{{f}_{3}} & =3\times \left( {\displaystyle \frac{v}{{4L}}} \right)=3\times 32\ \text{Hz}=96\ \text{Hz}\\{{f}_{5}} & =5\times \left( {\displaystyle \frac{v}{{4L}}} \right)=5\times 32\ \text{Hz}=160\ \text{Hz}\\{{f}_{7}} & =7\times \left( {\displaystyle \frac{v}{{4L}}} \right)=7\times 32\ \text{Hz}=224\ \text{Hz}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}=\displaystyle \frac{343\ \text{m.s}^{-1}}{392\ \text{Hz}}=0.875\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L\\\therefore L & =\displaystyle \frac{{{{\lambda }_{1}}}}{2}=\displaystyle \frac{{0.875\ \text{m}}}{2}=0.438\ \text{m}=43.8\ \text{cm}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}v & =f\times \lambda \\\therefore \lambda & =\displaystyle \frac{v}{f}=\displaystyle \frac{342\ \text{m.s}^{-1}}{176\ \text{Hz}}=1.94\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{\lambda }_{n}} & =\displaystyle \frac{{2L}}{n}\\\therefore {{\lambda }_{1}} & =2L\\\therefore L & =\displaystyle \frac{{{{\lambda }_{1}}}}{2}=\displaystyle \frac{{1.94\ \text{m}}}{2}=0.97\ \text{m}=97\ \text{cm}\end{align*}[/latex]
Media Attributions
- Img01_Constructive Interference © Siyavula is licensed under a CC BY (Attribution) license
- Img02_Destructive Interference © Siyavula is licensed under a CC BY (Attribution) license
- figure3 © DHET is licensed under a CC BY (Attribution) license
- figure4 © Andrew Duffy is licensed under a CC BY-NC (Attribution NonCommercial) license
- figure5 © DHET is licensed under a CC BY (Attribution) license
- figure6 © DHET is licensed under a CC BY (Attribution) license
- figure7 © DHET is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure8 © Pxhere is licensed under a CC0 (Creative Commons Zero) license
- activity3.1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.1.2a © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.1.2b © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.1.2c © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.1.2d © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.1.2e © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- activity3.2.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure9 © Y Landman is licensed under a Public Domain license
- figure10 © Labman Physics is licensed under a CC BY-SA (Attribution ShareAlike) license
harmonics: harmonics are waves with a frequency that is a positive integer multiple of the fundamental frequency of the original wave. The original wave is also called the 1st harmonic, with the following harmonics (2nd, 3rd, 4th, etc.) known as higher harmonics.
tuned mass dampers: also known as harmonic absorbers or seismic dampers, are devices mounted in structures such as tall buildings and even cars to reduce mechanical vibrations. A tuned mass damper consists of a mass that is mounted on one or more damped springs. The resonant frequency of the mass is tuned to be similar to that of the object it is mounted to. If the object starts to vibrate, the energy is transferred into the tuned mass damper.
