Waves, sound and light: Describe, analyse and apply principles of longitudinal waves in everyday life
Unit 1: Longitudinal waves
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Identify examples of longitudinal waves.
- Describe the production and propagation of longitudinal waves in various media.
- Describe and calculate:
- wave speed
- wavelength
- frequency
- amplitude.
- Differentiate between sound and radio waves.
What you should know
Before you start this unit, make sure you can:
- Identify and describe vibration and oscillation as a periodic motion.
- Define period, frequency and amplitude.
- Define a wave and identify different examples.
- Describe the nature of waves (a disturbance that travels and not the medium or energy that is carried or transferred.)
- Distinguish between the two categories of waves, longitudinal and transverse, and identify examples.
- Identify particle position on graphs showing displacement to illustrate difference between longitudinal and transverse waves.
- Draw, label and interpret a displacement position graph of a simple harmonic wave showing wavelength and amplitude.
- Calculate frequency, period and wave speed and wavelength of a transverse wave.
- Describe the effect of medium on wave speed.
- Distinguish between standing and moving waves
- Identify and describe superposition in standing waves.
Refer to level 2 subject outcomes 3.1 and 3.2 if you need help.
Transverse wave recap
Let’s start with a quick recap of transverse waves and their basic properties. Firstly, a wave is just a regular and repeated disturbance that takes place in a , resulting in a transfer of energy through the medium.
Transverse waves are probably the kind of waves you think about first when you think of waves. They are the waves (or ripples) we see on the surface of water (see figure 1).

In transverse waves the disturbance of the medium through which the wave travels is perpendicular (or at right-angles to) the direction of the wave itself. If the wave is moving horizontally (left to right as in figure 2), then the particles in the medium (the water droplets in water for example) move up and down.
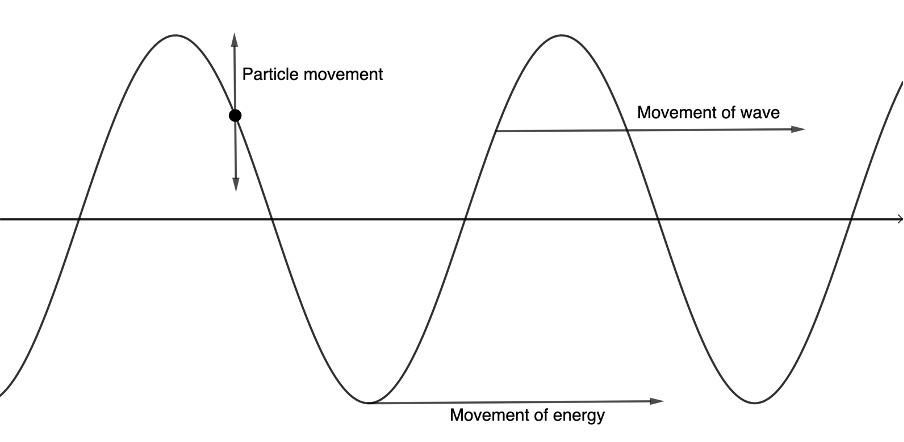
Figure 3 shows important properties of a transverse wave.
Take note!
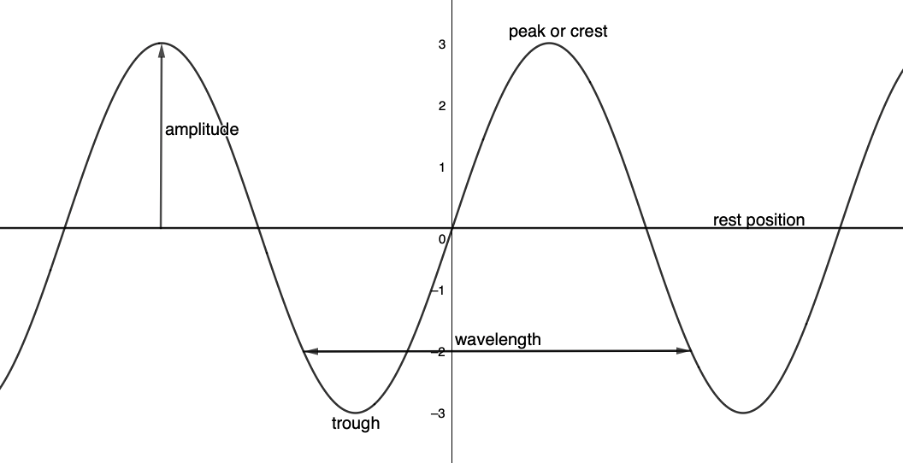
- The rest position is the position where the particles of the medium would be if there was no disturbance and no wave.
- The peak or crest is the highest point of displacement above the rest position.
- The trough is the lowest point of displacement below the rest position. The distance of the trough from the rest position is the same distance as the peak from the rest position.
- The amplitude is the height of the disturbance from the rest position. It is the distance of a peak or a trough from the rest position.
- The wavelength is the distance between any two consecutive points on a wave that are in phase (for example, the distance between successive peaks or troughs).
Light and radio waves are other examples of transverse waves. They can travel in a vacuum.
We will look at the properties of longitudinal waves in more detail in the next sections.
Longitudinal waves
A sound wave is an example of a longitudinal wave.
Activity 1.1: ‘See’ a sound wave
Time required: 10 minutes
What you need:
- a bowl
- some plastic cling film
- table salt
What to do:
- Pull the cling film over the top of the bowl so that it is very tight.
- Pour a little salt onto the cling film and spread it around.
- Now make a loud noise near the bowl. You can shout, clap your hands, bang on something or playing loud music. What happens to the salt?
- Why do you think the sound affects the salt in this way?
What did you find?
When you make a loud noise near the salt, you should see it vibrating. The salt vibrates because the cling film is vibrating. The cling film vibrates because the sound wave transfers its energy to the cling film.
The sound causes vibrations to travel through the air in the form of a longitudinal wave. This causes the air particles to vibrate backwards and forwards, passing the wave along. This causes the cling film to vibrate as it receives or ‘catches’ the sound wave. These vibrations make the salt vibrate as well.
This experiment clearly shows why we sometimes call longitudinal waves pressure waves. The change in pressure of the air particles caused by the sound makes the cling film and, hence, the salt vibrate. We can use these vibrations to transmit sounds.
Activity 1.2: Tin can telephone
Time required: 15 minutes
What you need:
- two tin cans or paper cups
- a nail
- a long piece of string (at least [latex]\scriptsize 3\ \text{m}[/latex])
- a friend to assist
What to do:
- Make a hole in the bottom of each of the tin cans or paper cups using the nail.
- Push one end of the piece of string through the bottom of one cup. Tie a knot on the inside so that the string will not slip out. Do the same with the other end of the string in the other cup.
- Take one of the cups and ask a friend to take the other one. Move apart from each other until the string is taut.
- Put the cup to your ear while your friend talks into the other cup. What do you hear?
- Now swop around and talk into your cup while your friend holds their cup to their ear. What happens?
What did you find?
When listening in your cup, you would have heard the sound of your friend’s voice coming from inside the cup. When they speak into their cup, the sound waves make vibrations. These vibrations travel through the air in the form of a longitudinal wave, causing the air particles to vibrate backwards and forwards. This causes the bottom of the cup to vibrate as well, and these vibrations then travel along the string. The string vibrations cause the bottom of your cup to vibrate which causes the air particles in your cup to vibrate. The pattern of these vibrations in your cup is the same as the patterns of vibrations in your friend’s cup and so you hear their voice.
Note
If you have an internet connection or were unable to do activity 1.2, watch the video called How to make a Paper Cup Phone.
The same basic principle we discovered in activity 1.2 is behind how all speakers, big and small, work. In the case of a speaker, an electrical signal is used to make an electromagnet move in and out of a round permanent magnet. This in-and-out vibration is amplified by the speaker’s diaphragm, which makes the air particles vibrate which makes the sound that we hear.
Note
If you have an internet connection, watch the video called How do speakers work? to see a simple demonstration.
The characteristics of longitudinal waves
Longitudinal waves have many of the same properties as transverse waves. However, there are two important differences.
The disturbance of the medium through which the wave travels is parallel to the direction of the wave itself not perpendicular as is the case for a transverse wave (left to right as in figure 4).
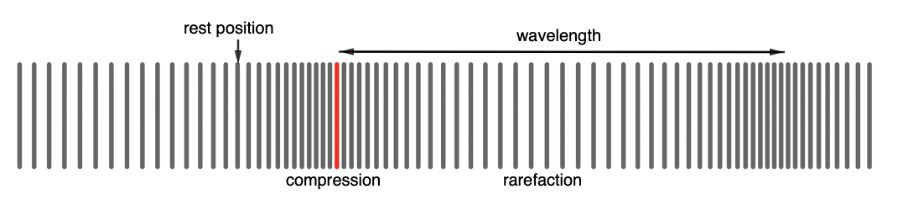
Instead of peaks or troughs like a transverse wave, longitudinal waves have compressions (areas of high pressure) and rarefactions (areas of low pressure). For this reason, longitudinal waves cannot travel through a vacuum; they can only travel through a medium. This is why no one can hear you scream in space!
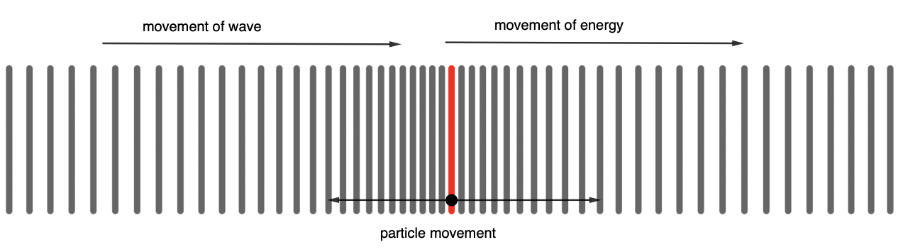
Note
If you have an internet connection, watch this animation of the motion of a longitudinal wave.
Like transverse waves, longitudinal waves also have a wavelength and an amplitude. As we will see in the next unit, these properties define what the sound wave sounds like to us.
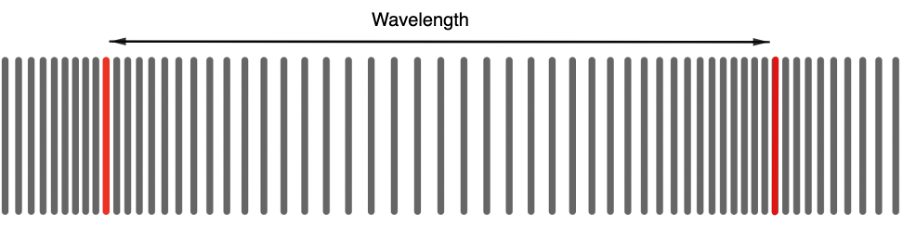
The wavelength of a longitudinal wave (denoted by [latex]\scriptsize \lambda[/latex]) is the distance between two consecutive points that are in phase (see figure 6). We usually take these two points as two compressions or two rarefactions, but the wavelength can be measured between any two in phase points. When we say ‘in phase’ we mean that the points are located at the same position in the wave cycle and are therefore separated by whole number of wavelengths.
Note
[latex]\scriptsize \lambda[/latex] is the Greek letter Lambda, and gives the ‘I’ sound.
Take note!
The wavelength ([latex]\scriptsize \lambda[/latex]) of a longitudinal wave is the distance between two consecutive points that are in phase. We usually measure wavelength in metres ([latex]\scriptsize \text{m}[/latex])
The amplitude of a longitudinal wave is the maximum displacement from equilibrium. For a longitudinal wave, which is a pressure wave, this means the maximum increase (or decrease) in the pressure that the particles in the medium experience when a compression (or rarefaction) passes through it.
Take note!
The amplitude of a longitudinal wave is a measure of the maximum increase (or decrease) in pressure from the equilibrium pressure of the medium.
Like transverse waves, we can also measure the period of longitudinal waves. The period is the time it takes for one full wavelength to pass a fixed point or for one particle in the medium to complete a full vibration cycle. We use capital [latex]\scriptsize T[/latex] as the symbol for period.
The frequency of longitudinal waves is a count of the number of wavelengths that pass a given point per second. We use cursive [latex]\scriptsize f[/latex] as the symbol for frequency
Take note!
The period ([latex]\scriptsize T[/latex]) of a wave is the time taken for one wavelength to pass a point.
The frequency ([latex]\scriptsize f[/latex]) of a wave is the number of wavelengths per second that pass a point.
Note
Period and frequency are closely related and can be confused. The frequency is how many times something happens in a given time. The period is how long it takes each of those things to happen. If you take three steps every second, then the frequency of your steps is three steps per second. However, to take three steps every second, each step must take one third of a second to complete. So, the period of one step is one third of a second.
The period of a wave is the inverse of its frequency. If four full wavelengths of a wave pass a point in one second (i.e. the frequency of the wave is [latex]\scriptsize 4\ \text{Hz}[/latex]), then each wave must take [latex]\scriptsize \displaystyle \frac{1}{2}[/latex] of a second to pass a point (i.e. the period is [latex]\scriptsize 0.25\ \text{s}[/latex]). We can relate period and frequency mathematically as follows:
[latex]\scriptsize f=\displaystyle \frac{1}{T}[/latex] or [latex]\scriptsize T=\displaystyle \frac{1}{f}[/latex]
Did you know?
The human ear can hear sound waves with a frequency of between about [latex]\scriptsize 20\ \text{Hz}[/latex] and [latex]\scriptsize 20\ \text{kHz}[/latex].
is like audible sound except it cannot be heard by humans because it has a frequency greater the [latex]\scriptsize 20\ \text{kHz}[/latex] (sometimes up to thousands of kHz or GHz).
, on the other hand, are sounds with a frequency too low for humans to hear.
Note
If you have an internet connection, watch the video called Transverse & Longitudinal Waves for a summary of the differences between transverse and longitudinal waves.
Speed of a longitudinal wave
If we know the wavelength of a wave and either it’s period or frequency, we can work out the speed at which the wave is travelling. The speed of a longitudinal wave is the distance travelled by one wave compression or rarefaction divided by the time taken to cover this distance. Therefore, the speed of a longitudinal wave is given by the formula [latex]\scriptsize v=f.\lambda[/latex], where:
[latex]\scriptsize v[/latex] is the speed of the wave, measured in metres per second ([latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex])
[latex]\scriptsize f[/latex] is the frequency, measured in hertz ([latex]\scriptsize \text{Hz}[/latex]) or ([latex]\scriptsize {{\text{s}}^{{\text{-1}}}}[/latex])
[latex]\scriptsize \lambda[/latex] is the wavelength of the wave, measured in metres ([latex]\scriptsize \text{m}[/latex])
Example 1.1
The musical note middle C has a frequency of [latex]\scriptsize 256\ \text{Hz}[/latex] and a wavelength of [latex]\scriptsize 131.87\ \text{cm}[/latex]. Calculate the speed at which the sound travels.
Solution
We need to calculate the speed. We are given two pieces of information – the frequency and the wavelength – and we know that [latex]\scriptsize v=f.\lambda[/latex].
Before calculating the speed, we need to make sure that the values are in the correct units. The frequency is already in hertz ([latex]\scriptsize \text{Hz}[/latex]) but the wavelength is in centimetres ([latex]\scriptsize \text{cm}[/latex]). We need to convert it into metres ([latex]\scriptsize \text{m}[/latex]).
[latex]\scriptsize \displaystyle \displaystyle \frac{{131.87\ \text{cm}}}{{100}}=1.3187\ \text{m}[/latex]
Now we can calculate the speed using the wave equation:
[latex]\scriptsize \displaystyle \begin{align*}v & =f.\lambda \\\therefore v & =256\ \text{Hz}\times 1.3187\ \text{m}\\ & =337.5872\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\ & =337.59\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\quad \text{Rounded to two decimal places}\end{align*}[/latex]
Example 1.2
A longitudinal wave is formed on a slinky so that it travels along the slinky with a speed of [latex]\scriptsize 15~\text{cm.s}^{-1}[/latex]. The distance between two consecutive rarefactions is [latex]\scriptsize 0.1\ \text{m}[/latex]. What is the frequency of this wave?
Solution
In this case, we are asked to determine the frequency of the wave. We are given the speed of the wave and its wavelength (the distance between two consecutive rarefactions). We know that [latex]\scriptsize v=f.\lambda[/latex] but we have to rearrange the equation to make [latex]\scriptsize f[/latex] the subject.
[latex]\scriptsize f=\displaystyle \frac{v}{\lambda }[/latex]
Before we use the wave equation, we need to make sure that they are in the correct units. The wavelength is already in metres ([latex]\scriptsize \text{m}[/latex]). The speed is in centimetres per second ([latex]\scriptsize \text{cm.s}^{-1}[/latex]). We need to convert it to metres per second ([latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]).
[latex]\scriptsize \displaystyle \frac{{15\ \text{cm}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{100}}=0.15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
Now we can use the wave equation:
[latex]\scriptsize \displaystyle \begin{align*}f&=\displaystyle \frac{v}{\lambda}\\\therefore f&=\displaystyle \frac{0.15\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}{{0.1\ \text{m}}}=1.5\ \text{Hz}\end{align*}[/latex]
Exercise 1.1
- Give an example of a transverse wave, and of a longitudinal wave.
- Draw a diagram of a longitudinal wave and label the following on your diagram:
- a compression
- a rarefaction
- the wavelength
- two points on the wave that are in phase with each other; use the letters A and B to label these points.
- A longitudinal wave is formed on a slinky so that it travels along the slinky with a speed of [latex]\scriptsize 30\ \text{cm.s}^{-1}[/latex]. The distance between three successive compressions is [latex]\scriptsize 1.85\times {{10}^{{-2}}}\ \text{m}[/latex].
- What is the wavelength of this wave?
- What is the frequency of the wave?
- What is the period of the wave?
- Five full wavelengths of a wave that has a length of [latex]\scriptsize 42\ \text{mm}[/latex] pass by a fixed point in a time of [latex]\scriptsize 4.8\ \text{s}[/latex]. Calculate the following for this wave:
- the frequency
- the period
- the speed.
- A longitudinal wave has a compression-to-compression distance of [latex]\scriptsize 12\ \text{m}[/latex]. It takes the wave [latex]\scriptsize 7\ \text{s}[/latex] to pass a point.
- What is the wavelength of the longitudinal wave?
- What is the speed of the wave?
- A sound wave passes from the air into water. If sound travels faster in water, how will this affect the following characteristics of the wave:
- the period?
- the wavelength?
The full solutions can be found at the end of the unit.
Summary
In this unit you have learnt the following:
- The rest position is the position in a longitudinal wave where the particles of the medium would be if there was no disturbance and no wave.
- A compression is a part of the longitudinal wave where the particles are closest together. In a compression, the particles are under the greatest pressure. This is why a longitudinal wave is sometimes called a pressure wave.
- The rarefaction is the part of the longitudinal wave where the particles are furthest apart. In a rarefaction, the particles are under the least pressure.
- The amplitude is the maximum increase (or decrease in pressure) that is caused when a compression (or rarefaction) passes a point.
- The wavelength is the distance between any two consecutive points on a wave that are in phase (for example, any two successive compressions or any two successive rarefactions).
- Longitudinal waves obey the basic wave equation [latex]\scriptsize v=f\times \lambda[/latex].
Unit 1: Assessment
Suggested time to complete: 15 minutes
- Which of the following can a longitudinal wave not travel through?
- solid
- liquid
- gas
- vacuum
- Which of the following is not an example of a longitudinal wave:
- sound travelling in water
- the sound of a train in a train track
- ultrasound
- radio waves
- A guitar produces a musical sound travelling at a speed of [latex]\scriptsize 333\ \text{m}\text{m.s}^{-1}[/latex]. The frequency of the note is [latex]\scriptsize 440\ \text{Hz}[/latex]. Calculate:
- the period of the note
- the wavelength of the note.
- Two learners form a longitudinal wave on a [latex]\scriptsize 2.5\ \text{m}[/latex] long slinky. The wave takes [latex]\scriptsize \displaystyle 1.85\ \text{s}[/latex] to move from one end of the slinky to the other. They tie a piece of string to the slinky and observe that it moves a total distance of [latex]\scriptsize 6.3\ \text{mm}[/latex] backwards and forwards. They also observe that the distance between four successive compressions is [latex]\scriptsize 72\ \text{cm}[/latex].
- Explain how they should move the slinky to create this wave.
- Find the speed of the wave.
- What is the wavelength of the wave?
- Work out the number of complete wavelengths that pass the piece of string in one second.
- Find the time that it takes for one complete wavelength to pass a fixed point.
- What is the amplitude of the wave?
- A sound wave with a frequency of [latex]\scriptsize 515\ \text{Hz}[/latex] travels [latex]\scriptsize 2.37\ \text{km}[/latex] through the air in [latex]\scriptsize 7.5\ \text{s}[/latex].
- Calculate the speed of sound in air.
- Calculate the period of this sound wave.
- Calculate the distance between two successive rarefactions of the sound wave.
The full solutions can be found at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- Transverse wave: light
Longitudinal wave: sound - .
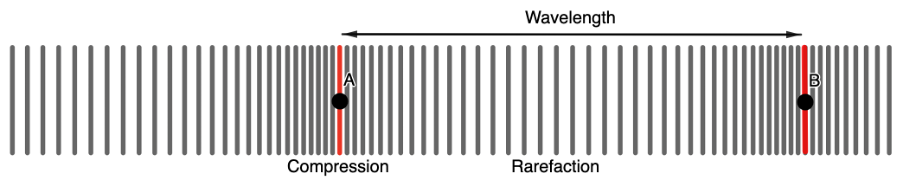
- .
- The distance between three successive compressions is [latex]\scriptsize 1.85\times {{10}^{{-2}}}\ \text{m}[/latex]. Therefore, the wavelength is [latex]\scriptsize 1.85\times {{10}^{{-2}}}\ \text{m}[/latex] or [latex]\scriptsize 0.0185\ \text{m}[/latex].
- [latex]\scriptsize v=30\ \text{cm.s}^{-1}=0.3\ \text{m.s}^{-1}[/latex]
[latex]\scriptsize \begin{align*}\lambda & =0.0185\ \text{m}\\v & =f\times \lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }\\ & =\displaystyle \frac{{0.3}}{{0.0185}}\\ & =16.22\ \text{Hz}\end{align*}[/latex] - [latex]\scriptsize T =\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{16.22}}=0.062\ \text{s}[/latex]
- .
- [latex]\scriptsize 5[/latex] waves pass in [latex]\scriptsize 4.8\ \text{s}[/latex]. Therefore, [latex]\scriptsize f=\displaystyle \frac{5}{{4.8\ \text{s}}}=1.042\ \text{Hz}[/latex].
- [latex]\scriptsize T =\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{1.042\ \text{Hz}}}=0.96\ \text{s}[/latex]
- [latex]\scriptsize 42\ \text{mm=0}\text{.042}\ \text{m}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}v & =f.\lambda \\\therefore v & =1.042\ \text{Hz}\times 0.042\ \text{m}\\ & =0.044\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
- A longitudinal wave has a compression-to-compression distance of [latex]\scriptsize 12 \text{m}[/latex]. It takes the wave [latex]\scriptsize 7 \text{s}[/latex] to pass a point.
- [latex]\scriptsize \lambda =12\ \text{m}[/latex]
- [latex]\scriptsize f=\displaystyle \frac{1}{7}=0.14\ \text{Hz}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}v & =f.\lambda \\\therefore v & =1.14\ \text{Hz}\times 12\ \text{m}\\ & =1.68\ \text{m.s}^{-1}\end{align*}[/latex]
- We know that the frequency of a longitudinal wave is determined by the vibrations of the source of the wave. This means that the frequency of a wave does not change even if the speed changes. Because the period is the inverse of the frequency, the period of a wave will also not change. Since [latex]\scriptsize v=f\times \lambda[/latex], if the speed of a wave changes then the wavelength of the wave must also change.
- The period, as the inverse of the frequency, does not change.
- [latex]\scriptsize v=f\times \lambda[/latex]. If [latex]\scriptsize f[/latex] does not change and the speed increases, this means the wavelength must decrease.
Unit 1: Assessment
- A longitudinal wave cannot travel through a vacuum.
- A radio wave is not a longitudinal wave
- .
- [latex]\scriptsize T=\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{400\ \text{Hz}}}=0.0025\ \text{s}[/latex]
- .
[latex]\scriptsize \begin{align*} v & =f. \lambda\\ \therefore \lambda&=\displaystyle \frac{v}{f}\\ &=\displaystyle \frac{333\ \text{m.s}^{-1}}{44~\text{Hz}}\\ & =0.76~\text{m}\end{align*}[/latex]
- .
- To create a longitudinal wave, they would need to move their hands backwards and forwards in the same direction as the spring.
- The wave takes [latex]\scriptsize 1.85\ \text{s}[/latex] to travel [latex]\scriptsize 2.5\ \text{m}[/latex].
[latex]\scriptsize \text{speed}=\displaystyle \frac{{\text{distance}}}{{\text{time}}}=\displaystyle \frac{{2.5\ \text{m}}}{{1.85\ \text{s}}}=1.35\ \text{m.s}^{-1}[/latex] - The distance between four successive compressions is [latex]\scriptsize 72\ \text{cm}[/latex]. Therefore, there are [latex]\scriptsize \displaystyle \frac{{72\ \text{cm}}}{3}=24\ \text{cm}[/latex] between each compression. Therefore, the wavelength is [latex]\scriptsize 24\ \text{cm}=0.24\ \text{m}[/latex].
- .
[latex]\scriptsize \begin{align*}v & =f.\lambda \\\therefore f & =\displaystyle \frac{v}{\lambda }\\ & =\displaystyle \frac{1.35\ \text{m.s}^{-1}}{0.24\ \text{m}}\\ & =5.63\ \text{Hz}\end{align*}[/latex] - [latex]\scriptsize T=\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{5.63\ \text{Hz}}}=0.18\ \text{s}[/latex]
- The amplitude is [latex]\scriptsize 6.3\ \text{mm}=0.0063\ \text{m}[/latex]
- A sound wave with a frequency of [latex]\scriptsize 515 \text{Hz}[/latex] travels [latex]\scriptsize 2.37 \text{km}[/latex] through air in [latex]\scriptsize 7.5 \text{s}[/latex].
- [latex]\scriptsize 2.37\ \text{km}=2\ 370\ \text{m}[/latex]
[latex]\scriptsize \text{speed}=\displaystyle \frac{{\text{distance}}}{{\text{time}}}=\displaystyle \frac{{2\ 370\ \text{m}}}{{7.5\ \text{s}}}=316\ \text{m.s}^{-1}[/latex] - [latex]\scriptsize T=\displaystyle \frac{1}{f}=\displaystyle \frac{1}{{515\ \text{Hz}}}=0.0019\ \text{s}[/latex]
- .
[latex]\scriptsize \begin{align*}v & =f.\lambda\\ \therefore \lambda & =\displaystyle \frac{v}{f}\\ & =\displaystyle \frac{316\ \text{m.s}^{-1}}{515\ \text{Hz}}\\ & =0.61\ \text{m}\end{align*}[/latex]
- [latex]\scriptsize 2.37\ \text{km}=2\ 370\ \text{m}[/latex]
Media Attributions
- figure1 © Pixabay is licensed under a Public Domain license
- figure2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure3 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- figure6 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- exercise3.1A2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
medium: the substance that a wave travels through
ultrasound: a sound that cannot be heard by humans because it has a frequency greater the 20 kHz (sometimes up to thousands of kHz or GHz)
infrasound: a sound that cannot be heard by humans because it has a frequency less than the 20 Hz
