Unit outcomes

By the end of this unit you will be able to:

• Define Newton’s second law of motion.
• Understand how Newton’s second law of motion applies.
• Plan and conduct a scientific investigation to investigate the proportionality between mass and acceleration.
• Use Newton’s second law to solve problems that involve a single object or multiple objects moving either horizontally or vertically.

What you should know

Before you start this unit, make sure you can:

• Draw vector diagrams for two forces acting on an object and determine the resultant. Revise subject outcome 2.2 unit 1 to help you with this.
• Determine the components of a force. Revise subject outcome 2.2 unit 2 to help you with this.
• Draw labelled free-body diagrams of objects in various situations. Revise subject outcome 2.2 unit 3 to help you with this.
• Draw free-body diagrams of parallel forces. Revise subject outcome 2.3 unit 2 to help you with this.
• Draw free-body diagrams of non-parallel forces. Revise subject outcome 2.3 unit 2 to help you with this.

Introduction

Parts of the text in this unit were sourced from Siyavula Physical Science Gr 11 Learner’s Book, Chapter 21, released under a CC-BY licence

In this unit you will extend your knowledge about the relationship between force and motion. You will learn how changing the applied force will affect an object’s motion and what the effect of the object’s mass is on its acceleration. This is described by Newton’s second law of motion. You will also investigate how Newton’s second law applies in practice and use your knowledge to solve problems in real-world settings.

Newton’s second law of motion

Newton’s second law of motion follows on from Newton’s first law, since it tells us how you can calculate the change of motion of an object as a result of a net force.

You can write Newton’s second law as a mathematical equation:
[latex]\scriptsize {{F}_{{net}}}=ma[/latex]

Where:

[latex]\scriptsize {{F}_{{net}}}[/latex] is the net force on an object, measured in the units newtons ([latex]\scriptsize \text{N}[/latex])

[latex]\scriptsize m[/latex] is the mass, measured in [latex]\scriptsize \text{kg}[/latex]

[latex]\scriptsize a[/latex] is the acceleration of the object, measured in [latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}[/latex]

Force is always measured in the units newtons ([latex]\scriptsize \text{N}[/latex]). [latex]\scriptsize 1\text{ N}[/latex] of force is the amount of force that will cause an object with a mass of [latex]\scriptsize 1\text{ kg}[/latex] to accelerate at [latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. So [latex]\scriptsize 1\text{ N = 1 kg}\text{.m}\text{.}{{\text{s}}^{{-2}}}[/latex].

Because acceleration is a vector quantity, force is also a vector quantity. The direction of the acceleration is always in the same direction as the net force. But remember that the direction of the acceleration is not always the direction of the motion.

• When the motion, net force and acceleration are all in the same direction, the object is speeding up.
• When the motion is in the opposite direction to the acceleration and net force, the object is slowing down.

Activity 2.1: Plan an investigation to find the relationship between mass and acceleration

Time required: 30 minutes

What you need:

• internet access
• graph paper

What to do:

1. Watch the video How to use a light gate, on how to measure the velocity of a moving object using a light gate.
   How to use a light gate – GCSE Physics (Duration: 01:55)
2. Watch the video Newton’s Second Law which shows an experiment to find the relationship between mass and acceleration when the force is constant.
   Newton’s Second Law – GCSE Physics (Duration: 03:40)
3. Design an experiment you could carry out to find the relationship between mass and acceleration if you had the equipment demonstrated in the two videos. You must include the following:
   • investigative question
   • hypothesis
   • independent variable and how you will vary it
   • dependent variable and how you will measure it
   • variables that need to be controlled and how you will control them
   • steps that will be taken to ensure reliability of results.
4. The data in the table below is a possible set of results that could be obtained for the experiment. Plot a graph of the data with mass on the [latex]\scriptsize x[/latex]-axis and acceleration on the [latex]\scriptsize y[/latex]-axis.
   .

   Mass ([latex]\scriptsize \text{kg}[/latex])	Acceleration ([latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{-2}}}[/latex])
   [latex]\scriptsize 0.5[/latex]	[latex]\scriptsize 0.82[/latex]
   [latex]\scriptsize 1.5[/latex]	[latex]\scriptsize 0.41[/latex]
   [latex]\scriptsize 2.0[/latex]	[latex]\scriptsize 0.27[/latex]
   [latex]\scriptsize 2.5[/latex]	[latex]\scriptsize 0.20[/latex]
   [latex]\scriptsize 3.0[/latex]	[latex]\scriptsize 0.16[/latex]

    

5. State the possible conclusion that can be drawn from the shape of your graph.
6. The mathematical relationship for variables that are inversely proportional is [latex]\scriptsize xy=k[/latex] where [latex]\scriptsize k[/latex] is a constant value. Using the data from the table, and this mathematical relationship, confirm that the relationship between mass and acceleration is an inverse proportion when the force is constant.

What did you find:

3. Design of investigation:
   • Investigative question: How does the mass affect the acceleration of an object when the force is constant?
   • Hypothesis: The acceleration will be inversely proportional to the acceleration when the force is kept constant.
   • Independent variable and how you will vary it: the mass of the trolley which will be varied by adding mass pieces to the trolley.
   • Dependent variable and how you will measure it: the acceleration which will be calculated using the formula [latex]\scriptsize a=\displaystyle \frac{{v-u}}{{\Delta t}}[/latex] using the [latex]\scriptsize u=0[/latex], [latex]\scriptsize v[/latex] measured by the light gate and using a stopwatch to measure [latex]\scriptsize \Delta t[/latex] from the start to when the trolley passes through the light gate
   • Variables that need to be controlled and how you will control them: the force on the trolley will be kept constant by keeping a fixed mass hanging on the string over the pulley.
   • Steps that will be taken to ensure reliability of results: for each mass, three measurements will be taken, and the average calculated.
4. Graph:
   
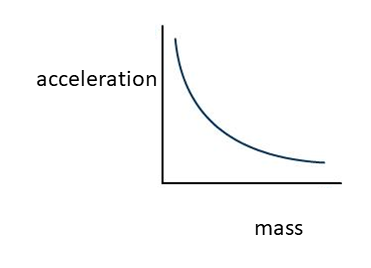
5. The shape of the graph indicates that the relationship could possibly be an inverse proportion.
6. Confirmation using data from the table:
   [latex]\scriptsize \begin{align*}&xy=k\\&\text{0}\text{.5 x 0}\text{.82 = 0}\text{.41}\\&\text{1}\text{.0 x 0}\text{.41 = 0}\text{.41}\\&\text{1}\text{.5 x 0}\text{.27 = 0}\text{.405}\\&\text{2}\text{.0 x 0}\text{.20 = 0}\text{.40}\\&\text{2}\text{.5 x 0}\text{.16 = 0}\text{.40}\end{align*}[/latex]
   Values are constant (within experimental error). This confirms that acceleration is inversely proportional to mass.

Applying Newton’s second law of motion

The following points should be kept in mind when you apply Newton’s second law to solve problems:

• When you apply the equation, [latex]\scriptsize {{F}_{{net}}}=ma[/latex] you need to identify all the forces acting on that object first. Only substitute the net force into this equation.
• Always draw a free body diagram showing all the forces acting on the object. This will enable you to use the equation, [latex]\scriptsize {{F}_{{net}}}={{F}_{1}}+{{F}_{2}}...[/latex] to find the net force.
• If all the forces acting on an object are in equilibrium, they balance each other out and the net force is zero. This means that the object will remain at rest or will travel with a constant velocity.
• If the forces on the object do not balance each other out (non-equilibrium), there is a net force on the object. This means that the object will have acceleration (it will be speeding up or slowing down).
• The components of the forces in the vertical (y) direction should be looked at separately to find [latex]\scriptsize {{F}_{{net\text{ }y}}}[/latex]. This can then be used to find the acceleration in the y direction: [latex]\scriptsize {{F}_{{net\text{ }y}}}=m{{a}_{y}}[/latex].
• Similarly, the forces in the horizontal (x) direction should be looked at separately to find [latex]\scriptsize {{F}_{{net\text{ }x}}}[/latex]. This can then be used to find the acceleration in the x direction: [latex]\scriptsize {{F}_{{net\text{ }x}}}=m{{a}_{x}}[/latex].

Example 2.1

A box with a mass of [latex]\scriptsize 5\text{ kg}[/latex] is being pushed along the ground in the [latex]\scriptsize x[/latex]– direction with a force of [latex]\scriptsize 30\text{ N}[/latex]. There is a frictional force of [latex]\scriptsize 10\text{ N}[/latex]between the box and the ground. Calculate the acceleration of the box.

Solution

Step 1: Draw a free body diagram of all the forces on the box You will only look at the forces acting on the box, since you want to calculate the acceleration of the box.

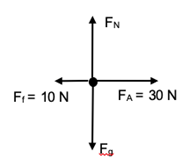
The forces perpendicular to the surface are in equilibrium, so [latex]\scriptsize {{F}_{{net\text{ }y}}}=0[/latex].

The net force parallel to the surface is not balanced.

Step 2: Calculate the [latex]\scriptsize {{F}_{{net\text{ }x}}}[/latex]

Start by choosing a direction as positive; to the right will be positive.

[latex]\scriptsize \begin{align*}{{F}_{{net\text{ }x}}}&={{F}_{A}}+{{F}_{f}}\\&=\text{30+(-10)}\\&=\text{20 N to the right}\end{align*}[/latex]

Step 3: Use Newton’s second law to find the acceleration

[latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\\text{ }20&=5a\\\text{ }a&=4\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ to the right}\end{align*}[/latex]

Exercise 2.1

1. An object with a mass of [latex]\scriptsize 150\text{ kg}[/latex] has an acceleration of [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] south. Calculate the magnitude of the net force on the object.
2. The net force on a [latex]\scriptsize 25\text{ kg}[/latex] object is [latex]\scriptsize 500\text{ N}[/latex] forward. Find the acceleration of the object.
3. A car with a mass of [latex]\scriptsize 800\text{ kg}[/latex] is being towed using a tow rope. The tension in the tow rope is [latex]\scriptsize 1\text{ 500 N}[/latex], and the acceleration of the car is [latex]\scriptsize 1.25\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. There is a frictional force between the car and the road surface. (Ignore the mass of the tow rope.)
   
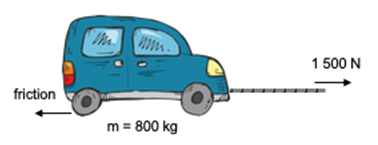
   1. Draw a free body diagram of all the forces acting on the car.
   2. Calculate the frictional force between the car and the road.
4. A car with a mass of [latex]\scriptsize 1\text{ 000 kg}[/latex] is being lifted vertically upward at a constant speed of [latex]\scriptsize 5\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] by a strong cable. The tension in the cable that is lifting the car is [latex]\scriptsize 10\text{ 000 N}[/latex]. There is an air resistance force acting on the car, and there are no horizontal forces acting on the car.
   1. Draw a free body diagram of the forces acting on the car.
   2. Calculate the magnitude of the air resistance force
5. Thomas gave a [latex]\scriptsize 50\text{ g}[/latex] ball a flick so that it rolled along a horizontal surface, and the ball eventually slowed down to a stop. If the frictional force between the ball and the surface is [latex]\scriptsize 0.2\text{ N}[/latex], calculate the acceleration of the ball.
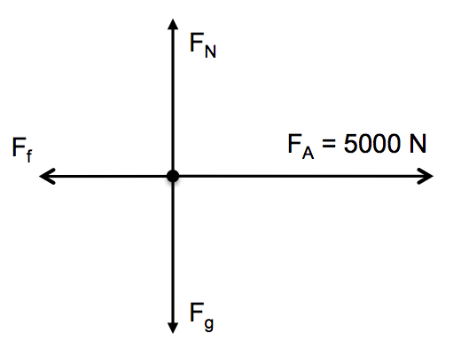
6. A car with a mass of [latex]\scriptsize 1\text{ 000 kg}[/latex] is pulled along a horizontal road with a force of [latex]\scriptsize 5\text{ 000 N}[/latex] to the right. There is a frictional force opposing the car’s movement. As a result, the net force on the car is [latex]\scriptsize 4\text{ 000 N}[/latex] to the right.
   1. Draw a free body diagram of all the forces acting on the car.
   2. Calculate the acceleration of the car.
   3. What is the magnitude and direction of the frictional force?
7. A car with a mass of [latex]\scriptsize 1.4\text{ x 1}{{\text{0}}^{3}}\text{ kg}[/latex] is being towed by a tow truck. The car is accelerating at a rate of [latex]\scriptsize 0.5\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. There is a frictional force of [latex]\scriptsize 200\text{ N}[/latex] between the car’s wheels and the road. What is the magnitude of the tension in the tow rope?
8. An object with a mass of [latex]\scriptsize 1.2\text{ kg}[/latex] is falling through the air with an acceleration of [latex]\scriptsize 9\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. What is the magnitude and direction of the force due to air resistance?

The full solutions are at the end of the unit.

Applying Newton’s second law when the applied force is at an angle

The definition of Newton’s second law states that the acceleration is in the same direction as the resultant force. If an object is accelerating horizontally, but the applied force is at an angle to the horizontal, the horizontal component, [latex]\scriptsize {{F}_{x}}[/latex], must be determined.

Example 2.2

A man is pulling a [latex]\scriptsize 20\text{ kg}[/latex] box with a rope that makes an angle of [latex]\scriptsize {{60}^{0}}[/latex] with the horizontal. If he applies a force of magnitude [latex]\scriptsize 150\text{ N}[/latex] and a frictional force of magnitude [latex]\scriptsize 15\text{ N}[/latex] is present, calculate the acceleration of the box.

Solution

Step 1: Draw a free body diagram

The motion is horizontal and therefore we will only consider the forces in a horizontal direction. Remember that vertical forces do not influence horizontal motion and vice versa.

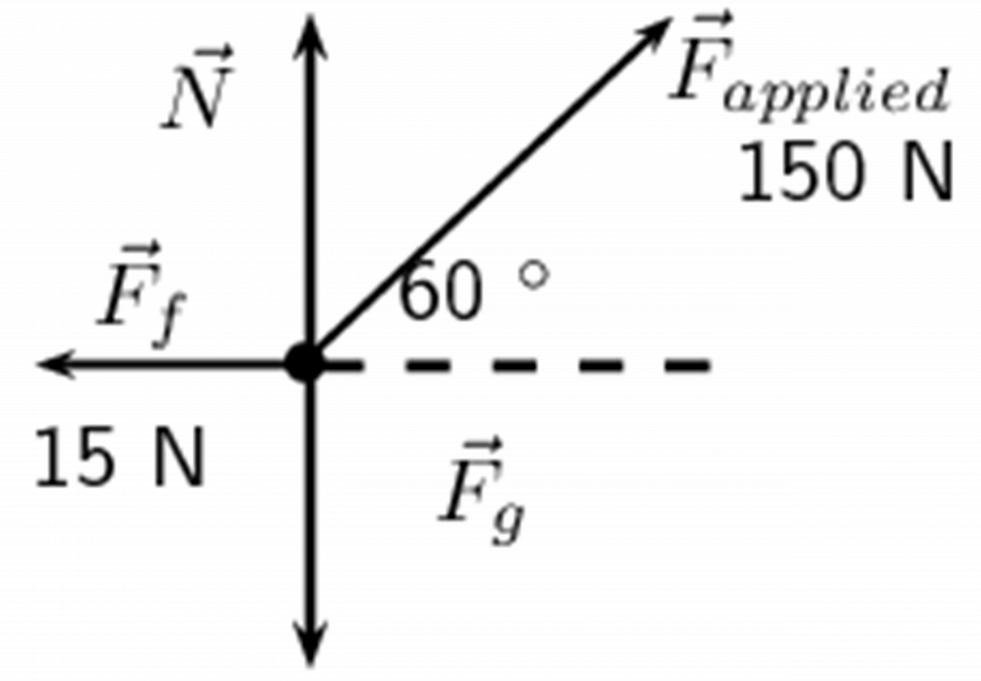
Step 2: Choose a direction as positive

Let the direction to the right be positive.

Step 3: Calculate the horizontal component ([latex]\scriptsize {{F}_{x}}[/latex]) of the applied force

The applied force is acting at an angle of [latex]\scriptsize {{60}^{0}}[/latex] to the horizontal. We can only consider forces that are parallel to the motion. The horizontal component of the applied force, [latex]\scriptsize {{F}_{x}}[/latex] ,needs to be calculated.

[latex]\scriptsize {{F}_{x}}={{F}_{A}}\cos \theta =150\cos {{60}^{0}}=75\text{ N to the right}[/latex]

Step 4: Determine the net force on the box

[latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{x}}+{{F}_{{}}}_{f}\\&=\text{75 + (-15)}\\&=\text{60 N }\end{align*}[/latex]

Step 5: Calculate the acceleration

To find the acceleration we apply Newton’s second law:

[latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\60&=20 \times a\\&=\text{3 m}\text{.}{{\text{s}}^{{-2}}}\text{ to the right}\end{align*}[/latex]

Exercise 2.2

1. Two forces act on a box as shown below. Calculate the acceleration of the box.
   
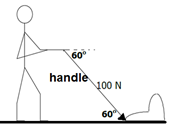
2. A man starts pushing a [latex]\scriptsize 17\text{ kg}[/latex] lawnmower with a force of [latex]\scriptsize 100\text{ N}[/latex]pushing down on the handle. The frictional force of the lawn is [latex]\scriptsize 18\text{ N}[/latex]. The handle makes an angle of [latex]\scriptsize {{60}^{0}}[/latex] with the ground. Calculate the acceleration of the lawnmower.
   
3. If a shopping trolley of mass [latex]\scriptsize 35\text{ kg}[/latex] accelerates down the aisle of a supermarket at [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] when it is pushed with a force of [latex]\scriptsize 80\text{ N}[/latex] acting at an angle of [latex]\scriptsize {{25}^{0}}[/latex] to the horizontal, calculate the frictional force acting on the trolley.

The full solutions are at the end of the unit.

Applying Newton’s second law of motion to objects on inclined planes (slopes)

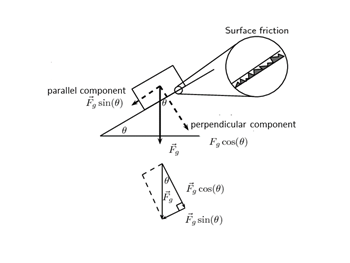
When we apply Newton’s second law to problems where objects are on an inclined plane, we need to include the component of the gravitational force parallel to the slope, because this will affect the resultant force on the object.

Think of a book on a table. As one side of the table is lifted higher the book starts to slide. Why? The book starts to slide because the component of the gravitational force parallel to the surface of the table gets larger for the larger angle of inclination. This is like the applied force, and it eventually becomes larger than the frictional force (acting upwards) and the book accelerates down the table or inclined plane.

Example 2.3

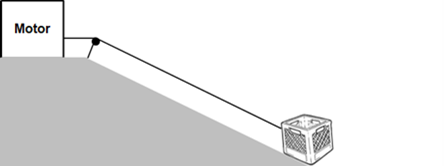
A crate is pulled up an inclined slope, moving from the bottom of the hill to the top. The crate has a mass of [latex]\scriptsize 50\text{ kg}[/latex]. The motor applies a force of [latex]\scriptsize 300\text{ N}[/latex] up the slope and the crate experiences a frictional force of [latex]\scriptsize 10\text{ N}[/latex]. The angle of inclination of the hill is [latex]\scriptsize {{31}^{0}}[/latex].

Calculate the acceleration of the crate.

Solution

Step 1: Draw a free body or force diagram for the crate

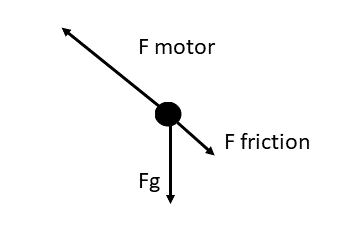
Step 2: Evaluate the forces that will affect the acceleration of the crate in the plane of the slope
[latex]\scriptsize {{F}_{{motor}}}=300\text{ N up the slope}[/latex]
[latex]\scriptsize {{F}_{{friction}}}=10\text{ N down the slope}[/latex]
[latex]\scriptsize {{F}_{x}}\text{ of }{{F}_{g}}=(50\text{ x 9}\text{.8)sin3}{{\text{1}}^{0}}=252.37\text{ N down the slope}[/latex]

Step 3: Choose a direction as positive and apply Newton’s second law

Let up the slope be positive.
[latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{{motor}}}+{{F}_{x}}+{{F}_{{}}}_{f}\\&=\text{800 + (}-\text{252}\text{.37)+(}-10)\\&=\text{536}\text{.63 N up the slope }\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&=ma\\537.63&=50 \times a\\&=\text{10}\text{.75 m}\text{.}{{\text{s}}^{{-2}}}\text{ up the slope}\end{align*}[/latex]

Exercise 2.3

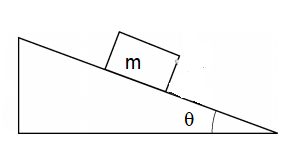
A box is sliding on a slope under various conditions. Calculate the acceleration for each set of conditions:

Condition 1:
[latex]\scriptsize \theta ={{20}^{0}}[/latex] no friction present, [latex]\scriptsize m=10\text{ kg}[/latex]

Condition 2:
[latex]\scriptsize \theta ={{35}^{0}}[/latex] , [latex]\scriptsize 10\text{ N}[/latex] friction with box moving down slope, [latex]\scriptsize m=20\text{ kg}[/latex]

Condition 3:
[latex]\scriptsize \theta ={{60}^{0}}[/latex] , [latex]\scriptsize 15\text{ N}[/latex] friction with box moving up slope, [latex]\scriptsize m=15\text{ kg}[/latex]

Condition 4:
[latex]\scriptsize \theta ={{30}^{0}}[/latex], [latex]\scriptsize 12\text{ N}[/latex] friction with girl pushing box up slope with a force 55 N, [latex]\scriptsize m=10\text{ kg}[/latex]

The full solution is at the end of the unit.

Applying Newton’s second law of motion to two connected objects

Newton’s second law can be applied to two connected objects moving horizontally or vertically. All objects in a connected system will have the same acceleration. These cases involve the force in a rope between the two objects, called tension. It is important to note that both ends of the rope apply a force with the same magnitude on each object, but it is opposite in direction. It is advisable to draw separate free body diagrams for each object.

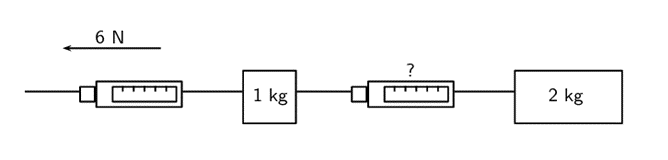
The spring balance will indicate that the magnitude of the force on the [latex]\scriptsize 2\text{ kg}[/latex] object and the [latex]\scriptsize 1\text{ kg}[/latex] object will be the same. The direction in which the force is exerted will be different: the force on the [latex]\scriptsize 2\text{ kg}[/latex] object will be to the left and the force on the [latex]\scriptsize 1\text{ kg}[/latex] object will be to the right.

Example 2.4

Two crates, [latex]\scriptsize 10\text{ kg}[/latex] and [latex]\scriptsize 15\text{ kg}[/latex] respectively, are connected with a thick rope according to the diagram.

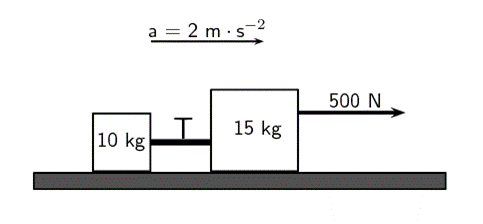
A force, to the right, of [latex]\scriptsize 500\text{ N}[/latex] is applied. The boxes move with an acceleration of [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] to the right. One third of the total frictional force is acting on the [latex]\scriptsize 10\text{ kg}[/latex] block and two thirds on the [latex]\scriptsize 15\text{ kg}[/latex] block.

Calculate:

1. the magnitude and direction of the total frictional force present
2. the magnitude of the tension in the rope at [latex]\scriptsize T[/latex].

Solutions

Step 1: Evaluate what is given

To make things easier let us give the two crates labels, let us call the [latex]\scriptsize 15\text{ kg}[/latex] crate number [latex]\scriptsize 1[/latex] and the [latex]\scriptsize 10\text{ kg}[/latex] crate number [latex]\scriptsize 2[/latex].

The fact that the crates are tied together with a rope means that they will both have the same acceleration. They will also both experience the same force due to the tension in the rope, but in opposite directions.

We are told that there is friction, but we are only given the relationship between the total frictional force both crates experience and the fraction each one experiences. The total friction will be the sum of the friction on crate 1 and the friction on crate 2. We know the blocks are accelerating to the right and we know that friction will be in the direction opposite to the direction of motion and parallel to the surface.

Step 2: Draw free body or force diagrams

The diagram for crate [latex]\scriptsize 1[/latex] will be:

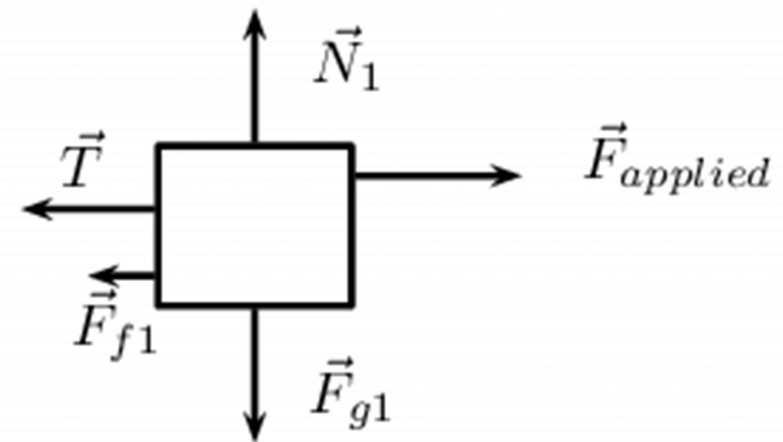
The diagram for crate [latex]\scriptsize 2[/latex] will be:

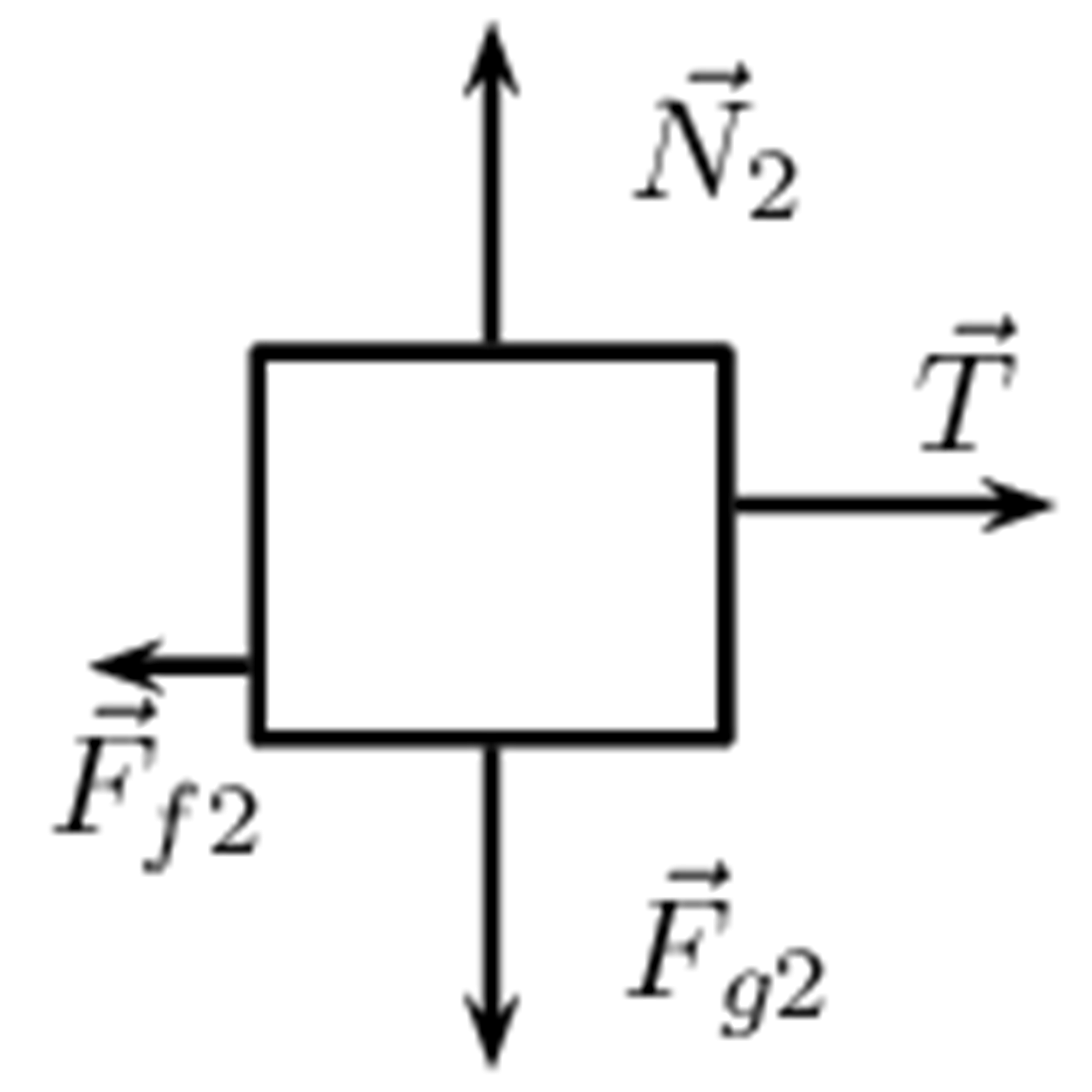
Step 3: Apply Newton’s second law of motion

The problem tells us that the crates are accelerating along the [latex]\scriptsize x[/latex]-direction which means that the forces in the [latex]\scriptsize y[/latex]-direction do not result in a net force. Let to the right be positive.

We can now apply Newton’s second law of motion to each crate.

For crate [latex]\scriptsize 1[/latex]:
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 1}}}}\text{ }&=ma\\&=15\times 2\\&=\text{30 N right}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 1}}}}&={{F}_{A}}+{{F}_{{f\text{ 1}}}}+T\\30&=\text{500+(}\displaystyle \frac{2}{3}{{F}_{f}})+(-T) & \text{Note that }T \text{ on crate 1 is to the left, } \\&&\text{so it must be negative}\\T&=470+\displaystyle \frac{2}{3}{{F}_{f}}......eqtn\text{ 1}\end{align*}[/latex]

Now apply Newton’s second law of motion to the crate 2:
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 2}}}}\text{ }&=ma\\&=\text{10 x 2}\\&=\text{20 N right}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 2}}}}&=T+{{F}_{{f\text{ 2}}}}\\20&=T\text{+}\displaystyle \frac{1}{3}{{F}_{f}}\\T&=20-\text{ }\displaystyle \frac{1}{3}{{F}_{f}}......eqtn\text{ 2}\end{align*}[/latex]

Step 4: Solve simultaneous equations

We have used Newton’s second law of motion to create two equations with two unknowns, this means we can solve simultaneously.

[latex]\scriptsize \begin{align*}470+\displaystyle \frac{2}{3}{{F}_{f}}&=20-\displaystyle \frac{1}{3}{{F}_{f}}\\\displaystyle \frac{2}{3}{{F}_{f}}+\displaystyle \frac{1}{3}F&=20-470\\\text{ }{{F}_{f}}&=-450\\\text{ }{{F}_{f}}&=450\text{ N to the left}\end{align*}[/latex]

Step 5: Substitute the total friction force into either of the equations to find the tension in the rope

[latex]\scriptsize \begin{align*}T&=\text{470 +}\displaystyle \frac{2}{3}{{F}_{f}}\\&=\text{470 + }\displaystyle \frac{2}{3}(-450)\\&=\text{170 N}\end{align*}[/latex]

Example 2.5

A crane is lifting a [latex]\scriptsize 30\text{ kg}[/latex] mass and a [latex]\scriptsize 50\text{ kg}[/latex] mass vertically as in the diagram. If they accelerate upwards at [latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex], calculate the values of tension [latex]\scriptsize T1[/latex] and [latex]\scriptsize T2[/latex](ignore air friction).

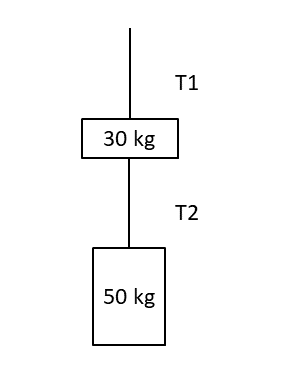
Solution

Step 1: Evaluate the question

To make things easier let us give the two crates labels, let us call the [latex]\scriptsize 30\text{ kg}[/latex] crate number 1 and the [latex]\scriptsize 50\text{ kg}[/latex] crate number 2.

The fact that the crates are tied together with a rope means that they will both have the same acceleration ([latex]\scriptsize 1\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]up). They will also both experience the same force due to the tension [latex]\scriptsize T2[/latex], but in opposite directions.

Step 2: Draw force or free body diagrams

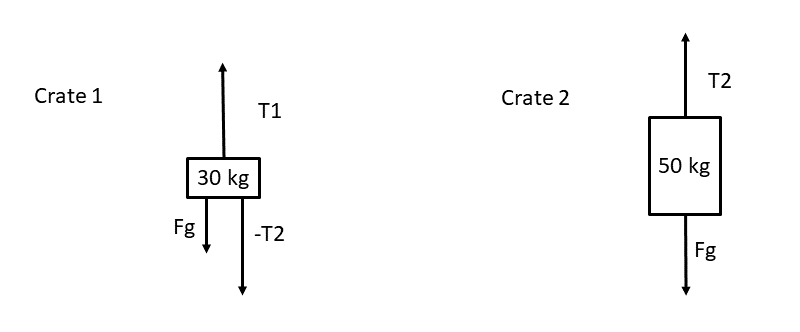
Step 3: Apply Newton’s second law of motion

The problem tells us that the crates are accelerating along the [latex]\scriptsize y[/latex]-direction. There are no forces in the [latex]\scriptsize x[/latex]-direction. Let up be positive.

We can now apply Newton’s second law of motion to each crate.

For crate 2:
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 2}}}}\text{ }&=ma\\&=50 \times 1\\ &=50{ N up}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 2}}}}&=\text{ }T\text{2}+{{F}_{g}}\\50&=T\text{2 +(50 x }-\text{9}\text{.8)}\\2&=490+50 && \text {note that }T2 \text{ on crate 2 is up}\\&=\text{540 N }\end{align*}[/latex]

For crate 1:
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 1}}}}\text{ }&=ma\\&=\text{30 x 1}\\&=\text{30 N up}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{F}_{{net\text{ 2}}}}&=T1+(-T2)+{{F}_{g}}\\30&=T\text{1+(}-540)+(30\text{ x }-9.8)\\T\text{1}& =30+540+294 && \text{note that } T2 \text{ on crate 1 is down}\\T\text{1}&=\text{840 N up}\end{align*}[/latex]

Exercise 2.4

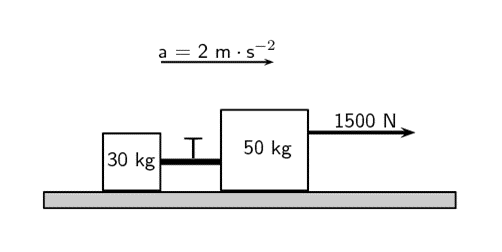
1. Two boxes of [latex]\scriptsize 30\text{ kg}[/latex] and [latex]\scriptsize 50\text{ kg}[/latex] are connected with a rope as in the diagram below. A force to the right of [latex]\scriptsize 1\text{ }500\text{ N}[/latex] is applied. The boxes move with an acceleration of [latex]\scriptsize \text{2 m}\text{.}{{\text{s}}^{{-2}}}[/latex] to the right. The frictional force on each block is in the same ratio as their masses. Calculate the total frictional force on the two boxes.
   
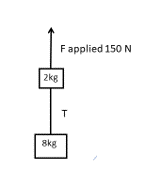
2. Two objects of [latex]\scriptsize 2\text{ kg}[/latex] and [latex]\scriptsize 8\text{ kg}[/latex] are accelerated upward by an applied force of [latex]\scriptsize 150\text{ N}[/latex]. Calculate the acceleration and the tension [latex]\scriptsize T[/latex] in the rope connecting them.
   

The full solutions are at the end of the unit.

Summary

• Newton’s second law states that when a net force is applied to an object of mass, the object accelerates in the direction of the net force. The acceleration is directly proportional to the net force and inversely proportional to the mass.
• You can write Newton’s second law as an equation: [latex]\scriptsize {{F}_{{net}}}=ma[/latex].
• This equation, as well as the equation for finding a net force using vector addition ([latex]\scriptsize {{F}_{{net}}}={{F}_{1}}+{{F}_{2}}...[/latex]) can be used to solve problems for horizontal motion, vertical motion, objects moving on inclined planes and when two or more objects are linked together and moving as one system.
• It is important to always draw a free body or force diagram when solving these problems.

Unit 2: Assessment

Suggested time to complete: 40 minutes

1. A sports car (mass [latex]\scriptsize 1\text{ 000 kg}[/latex]) is able to accelerate uniformly from rest to [latex]\scriptsize 30\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in [latex]\scriptsize 6\text{ s}[/latex].
   1. Calculate the magnitude of the acceleration of the car.
   2. What is the magnitude of the resultant force acting on the car during these [latex]\scriptsize 6\text{ s}[/latex]?
   3. The magnitude of the force that the wheels of the vehicle exert on the road surface as it accelerates is [latex]\scriptsize 7\text{ 500 N}[/latex]. What is the magnitude of the retarding forces acting on this car?
2. A braking test is carried out on a car travelling at [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. A braking distance of [latex]\scriptsize 30\text{ m}[/latex] is measured when a total braking force of [latex]\scriptsize 6\text{ 000 N}[/latex] stops the car.
   1. Calculate the acceleration of the car.
   2. Show that the mass of this car is [latex]\scriptsize 900\text{ kg}[/latex].
3. A box is being lifted by a [latex]\scriptsize 200\text{ N}[/latex] force. Ignore air resistance.
   
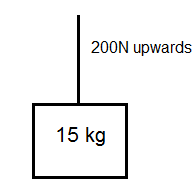
   1. Calculate the net force on the box.
   2. Calculate the acceleration of the box.
4. A pallet with bricks is being lifted vertically by a crane. The pallet and bricks have a combined mass of [latex]\scriptsize 2\text{ 000 kg}[/latex]. The pallet and bricks move upwards at an acceleration of [latex]\scriptsize 0.03\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. Calculate the tension in the cable during this time.
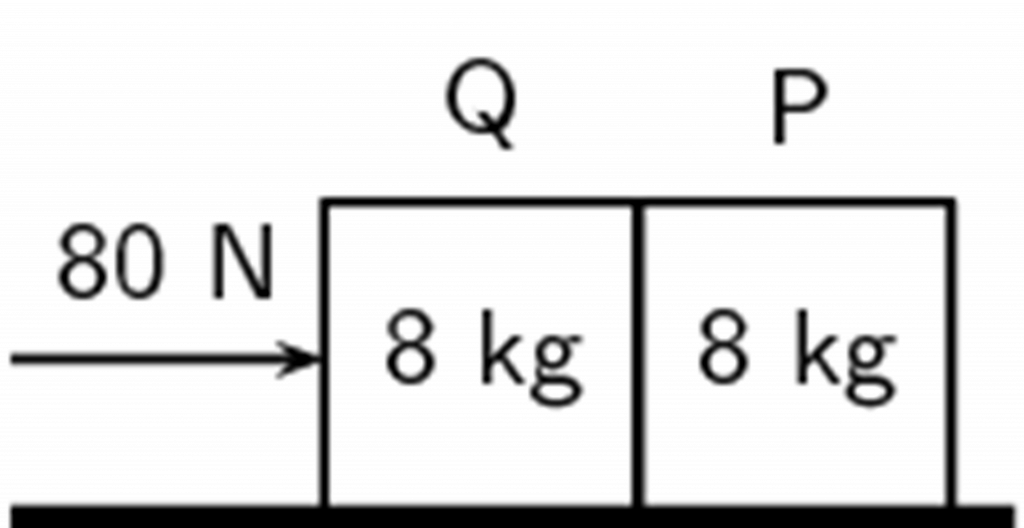
5. Two crates, Q and P, are pushed by a force of [latex]\scriptsize 80\text{ N}[/latex] along a rough surface. The frictional force acting on each block is [latex]\scriptsize 5\text{ N}[/latex].
   1. Calculate the acceleration of the blocks.
   2. Calculate the force that P exerts on Q.
      
6. A rocket (mass [latex]\scriptsize 20\text{ 000 kg}[/latex]) accelerates at [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] in the first [latex]\scriptsize 1.6\text{ s}[/latex] of its journey upwards into space. What is the magnitude of the total thrust exerted on the rocket during this time? (Ignore the effects of air friction.)
7. Car A is towing Car B with a light tow rope. Car A and B are identical. The cars move along a straight, horizontal road.
   1. Write down a statement of Newton’s second law of motion (in words).
   2. As they start off, Car A exerts a forward force of [latex]\scriptsize 600\text{ N}[/latex] at its end of the tow rope. The force of friction on Car B when it starts to move is [latex]\scriptsize 200\text{ N}[/latex]. The mass of Car B is [latex]\scriptsize 1\text{ 200 kg}[/latex]. Calculate the acceleration of Car B.
   3. Calculate the applied force exerted by the engine of Car A.
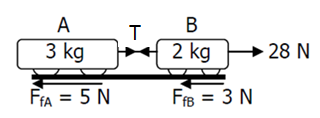
8. Two trolleys are joined by a light string as shown in the diagram. Calculate the acceleration of the system and the tension [latex]\scriptsize T[/latex].
   
9. A block of mass [latex]\scriptsize 240\text{ kg}[/latex] accelerates down an inclined plane at a rate of [latex]\scriptsize 1.5\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. The frictional force acting on the block is [latex]\scriptsize 49\text{ N}[/latex]. Calculate the inclination of the plane [latex]\scriptsize \theta[/latex].
   
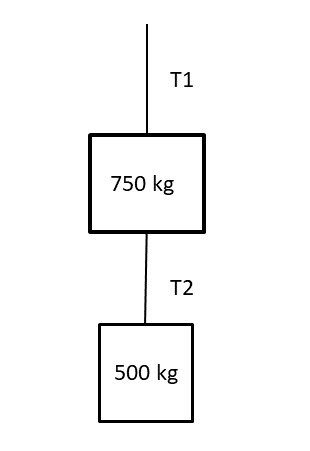
10. A crane is lowering two crates of bricks connected by a cable in which the tension ([latex]\scriptsize T2[/latex]) is [latex]\scriptsize 500\text{ N}\text{. }[/latex]The crates of bricks have masses of [latex]\scriptsize 750\text{ kg}[/latex] and [latex]\scriptsize 500\text{ kg}[/latex] as shown in the diagram. Calculate the acceleration of the crates and the tension in the upper cable ([latex]\scriptsize T1[/latex]).
    

The full solutions are at the end of the unit.

Unit 2: Solutions

Exercise 2.1

1. [latex]\scriptsize m=150~\text{kg}[/latex], [latex]\scriptsize a=2~\text{m.s}^{-2}[/latex]. Let south be positive
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{150 x 2}\\&=\text{300 N south}\end{align*}[/latex]
2. [latex]\scriptsize {{F}_{{net}}}=500~\text{N}[/latex], [latex]\scriptsize m=25~\text{kg}[/latex]. Let forward be positive
   [latex]\scriptsize \begin{align*} {{F}_{{net}}}&=ma\\ 500&=25 \times a\\ a&=20~\text{m.s}^{-2}~\text{ forward} \end{align*}[/latex]
3. .
   1. .
      
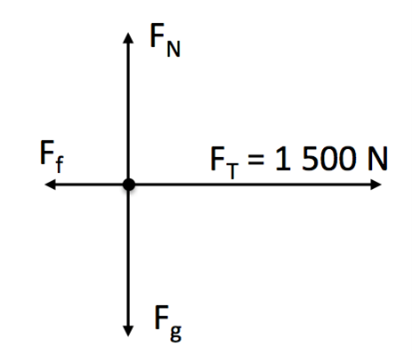
   2. You first need to calculate the net force using the acceleration:
      Let forward be positive.
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{800 x 1}\text{.25}\\&=\text{1 000 N}\end{align*}[/latex]
      The forces in the [latex]\scriptsize y[/latex] direction are in equilibrium, so you do not need to use these to calculate the frictional force.
      In the x direction:
      [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{T}}+{{F}_{{}}}_{f}\\\text{1 000}&= \text{1500 + }{{F}_{f}}\\&=\text{-500 N }\\&=\text{500 N in the opposite direction}\end{align*}[/latex]
4. .
   1. The direction of the air resistance force is down since it opposes the upward motion of the car.
      
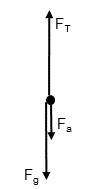
   2. [latex]\scriptsize {{F}_{{net\text{ }x}}}=0[/latex] since there are no horizontal forces.
      The direction of motion is upward, so choose up as the positive direction.
      The vertical speed is constant, so [latex]\scriptsize a=0[/latex].
      Therefore [latex]\scriptsize {{F}_{{net}}}=ma=0[/latex]
      But [latex]\scriptsize {{F}_{{net}}}={{F}_{T}}+{{F}_{g}}+{{F}_{a}}[/latex].
      [latex]\scriptsize {{F}_{g}}=mg=1\text{ 000 x -9}\text{.8 = -9 800 N}[/latex]
      Therefore:
      [latex]\scriptsize \begin{align*}\text{ }0&=10\text{ 000 + (-9 800) + }{{F}_{a}}\\{{F}_{a}}&=\text{ -200 N }\\&=\text{200 N down}\end{align*}[/latex]
5. [latex]\scriptsize {{F}_{f}}=-0.2\text{ N}[/latex] (friction is negative as it opposes the motion)
   [latex]\scriptsize m=50\text{ g }\div \text{ 1 000 = 0}\text{.05 kg}[/latex]
   Since there are no other unbalanced forces on the ball, [latex]\scriptsize {{F}_{{net}}}={{F}_{f}}=-0.2\text{ N}[/latex].
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&=ma\\-0.2&=0.05a\\\text{ }a&=-4\text{ m}\text{.}{{\text{s}}^{{-2}}}\\&=\text{4 m}\text{.}{{\text{s}}^{{-2}}}\text{ in the opposite direction}\end{align*}[/latex]
6. .
   1. .
      
   2. .
      [latex]\scriptsize \displaystyle \begin{align*}\text{ }{{F}_{{net}}}&=ma\\\text{4 000}&= \text{1 000 x }a\\a&=\text{4 m}\text{.}{{\text{s}}^{{-2}}}\text{ right}\end{align*}[/latex]
   3. Choose right as positive.
      [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{A}}+{{F}_{f}}\\4\text{ 000 }&= \text{5 000 + }{{\text{F}}_{f}}\\\text{ }{{F}_{f}}&=\text{-1 000 N}\\&=\text{1 000 N left}\end{align*}[/latex]
7. Free body diagram of the forces:
   
   .
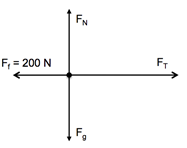
   [latex]\scriptsize m=1.4\text{ x 1}{{\text{0}}^{3}}\text{ kg}[/latex] [latex]\scriptsize a=\text{ 0}\text{.5 m}\text{.}{{\text{s}}^{{-2}}}[/latex]
   Choose forward as positive:
   [latex]\scriptsize \displaystyle \begin{align*}{{F}_{{net}}}&=ma\\&=\text{(1}\text{.4 x 1}{{\text{0}}^{3}}\text{) x 0}\text{.5}\\&=\text{700 N forward}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{T}}+{{F}_{f}}\\700&={{F}_{T}}+(-200)\\\text{ }{{F}_{T}}&=\text{ 900 N forward}\end{align*}[/latex]
8. Free body diagram of the forces:
   
   .
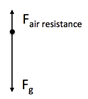
   Choose down as positive (you usually choose the direction of motion as the positive direction in your frame of reference).
   [latex]\scriptsize {{F}_{g}}=mg=1.2\text{ x 9}\text{.8 = 11}\text{.76 N}[/latex] [latex]\scriptsize a=9\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]
   [latex]\scriptsize \displaystyle \begin{align*}{{F}_{{net}}}&=ma\\&=\text{1}\text{.2 x 9}\\&=\text{10}\text{.8 N down}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{g}}+{{F}_{a}}\\10.8&=\text{ 11}\text{.76}+{{F}_{a}}\\\text{ }{{F}_{a}}&=\text{ 0}\text{.96 N up}\end{align*}[/latex]

Back to Exercise 2.1

Exercise 2.2

1. [latex]\scriptsize {{F}_{x}}={{F}_{A}}\cos \theta =200\cos {{30}^{0}}=173.21\text{ N to the right}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{x}}+{{F}_{{}}}_{f}\\&=\text{173}\text{.21 + (}-200\text{)}\\&=\text{ }-26.79\text{ N }\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\-\text{26}\text{.79}&= \text{20 x }a\\a&=-1.34\\&=\text{1}\text{.34 m}\text{.}{{\text{s}}^{{-2}}}\text{ to the left}\end{align*}[/latex]
2. [latex]\scriptsize {{F}_{x}}={{F}_{A}}\cos \theta =100\cos {{60}^{0}}=50\text{ N to the right}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{A}}+{{F}_{{}}}_{f}\\&=\text{50 + (}-18\text{)}\\&=\text{32 N right }\\ {{F}_{{net}}}&=ma\\\text{32}&= \text{17 x a}\\\text{ }a&=1.88\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ to the right}\end{align*}[/latex]
3. .
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{35 x 2}\\&=\text{70 N}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=F_{A}+F_{f}\\70&=80+F_{f}\\F_{f}&=-10 \text{ N}\\&=10 \text{ N in the opposite direction}\end{align*}[/latex]

Back to Exercise 2.2

Exercise 2.3

Let down the slope be positive.

Condition 1:

[latex]\scriptsize \begin{align*}{{F}_{x}}\text{ of }{{F}_{g}}&=(10\text{ x 9}\text{.8)sin2}{{\text{0}}^{0}}\\&=\text{33}\text{.52 N down the slope}\\\text{ }{{F}_{{net}}}={{F}_{x}}&=ma\\\text{ 33}\text{.52}&= \text{10}a\\\text{ }a&=3.35\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{down the slope}\end{align*}[/latex]

Condition 2:

[latex]\scriptsize \begin{align*}{{F}_{x}}\text{ of }{{F}_{g}}&=(20\text{ x 9}\text{.8)sin3}{{\text{5}}^{0}}\\&=\text{112}\text{.42 N down the slope}\\\text{ }{{F}_{{net}}}&={{F}_{x}}+{{F}_{f}}\text{ }\\&=\text{112}\text{.42 +(}-10)\\&=\text{102}\text{.42 N}\\\text{ }{{F}_{{net}}}&=ma\\\text{102}\text{.42}&=\text{20}a\\a&=5.12\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ down the slope}\end{align*}[/latex]

Condition 3:

[latex]\scriptsize \begin{align*}{{F}_{x}}\text{ of }{{F}_{g}}&=(15\text{ x 9}\text{.8)sin6}{{\text{0}}^{0}}\\&=\text{112}\text{.31 N down the slope}\\\text{ }{{F}_{{net}}}&={{F}_{x}}+{{F}_{f}}\text{ }\\&=\text{127}\text{.31+}15 && \text{friction is positive because the object is moving up the slope}\\&=\text{142}\text{.31 N down the slope}\\\text{ }{{F}_{{net}}} &=ma\\\text{142}\text{.31}&=\text{15}a\\a& =9.49\text{ m}\text{.}{{\text{s}}^{{-2}}}\text{ down the slope}\end{align*}[/latex]

Note: this object will be slowing down because acceleration is in the opposite direction to the motion.

Condition 4:

[latex]\scriptsize \begin{align*}{{F}_{x}}\text{ of }{{F}_{g}}&=(10\text{ x 9}\text{.8)sin3}{{\text{0}}^{0}}\\&=\text{49 N down the slope}\\\text{ }{{F}_{{net}}}&={{F}_{x}}+{{F}_{f}}\text{+}{{F}_{A}}\text{ }\\&=\text{49 +}12+(-55)\\&=-\text{6 N}\\\text{ }{{F}_{{net}}}&=ma\\\text{ }-\text{6}&= \text{10}a\\\text{ }a&=-0.6\\&=\text{0}\text{.6 m}\text{.}{{\text{s}}^{{-2}}}\text{ up the slope}\end{align*}[/latex]

Back to Exercise 2.3

Exercise 2.4

1. Let to the right be positive.
   For the [latex]\scriptsize 30\text{ kg}[/latex] box:
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}\text{ }&=ma\\&=\text{30 x 2}\\&=\text{60 N right}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=T+\displaystyle \frac{{30}}{{80}}{{F}_{f}}\\\text{ 60}&=T\text{+(}\displaystyle \frac{{30}}{{80}}{{F}_{f}})\\\text{ }T&=\text{60}-(\displaystyle \frac{{30}}{{80}}{{F}_{f}})......eqtn\text{ 1}\end{align*}[/latex]
   .
   For the [latex]\scriptsize 50\text{ kg}[/latex] box:
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}\text{ }&=ma\\&=\text{50 x 2}\\&=\text{100 N right}\end{align*}[/latex]
   Solve simultaneously:
   [latex]\scriptsize \begin{align*}\text{60}-(\displaystyle \frac{{30}}{{80}}{{F}_{f}})&=\text{1400}-(\displaystyle \frac{{30}}{{80}}{{F}_{f}})\\-{{F}_{f}}&=1400-60\\\text{ }{{F}_{f}}&=1340\text{ N to the left}\end{align*}[/latex]
2. Let up be positive.
   For the [latex]\scriptsize \text{2 kg}[/latex] mass:
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{A}}+{{F}_{g}}+(-T)\\\text{ }ma&=150+(2\text{ x }-9.8)-T\\2(a)&=130.4-T...eqtn\text{ 1}\end{align*}[/latex]
   For the [latex]\scriptsize \text{8 kg}[/latex] mass:
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&=T+{{F}_{g}}\\\text{ }ma&=T+(6\text{ x }-9.8)\\\text{ 8}(a)&=T-78.4...eqtn\text{ 2}\end{align*}[/latex]
   Solve simultaneously:
   [latex]\scriptsize \begin{align*}2a+8a&=(130.4-T)+(T-78.4)\\\text{ 10a}&= \text{52}\\\text{ a}&= \text{5}\text{.2 m}\text{.}{{\text{s}}^{2}}\text{ up}\end{align*}[/latex]
   To find tension, substitute into either equation 1 or equation 2:
   [latex]\scriptsize \begin{align*}\text{ }2a&=130.4-T\\2(5.12)&=130.4-T\\\text{ }T&=120.16\text{ N}\end{align*}[/latex]

Back to Exercise 2.4

Unit 2: Assessment

1. .
   1. .
      [latex]\scriptsize \begin{align*}u&=0\text{ }   v=30\text{ m}\text{.}{{\text{s}}^{{-1}}}   \text{ }\Delta t\text{ = 6s}\\a&=\displaystyle \frac{{v-u}}{{\Delta t}}\\&=\displaystyle \frac{{30-0}}{6}\\&=\text{5 m}\text{.}{{\text{s}}^{{-2}}}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{1000 x 5}\\&=\text{5 000 N}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{A}}+{{F}_{f}}\\5\text{ 000}&= \text{7 500 + }{{F}_{f}}\\\text{ }{{F}_{f}}&=\text{-2 500}\\&=\text{2 500 N in the opposite direction to motion}\end{align*}[/latex]
2. .
   1. .
      [latex]\scriptsize \begin{align*}u&=20\text{ m}\text{.}{{\text{s}}^{{-1}}}   s=30\text{ m }   v\text{ = 0}\\{{v}^{2}}&={{u}^{2}}+2as\\0&={{20}^{2}}+2(a)(30)\\a&=-6.67\\&=\text{6}\text{.67 m}\text{.}{{\text{s}}^{{-2}}}\operatorname{in}\text{ the opposite direction}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&=ma\\-6000&=m(-6.67)\\\text{ }m&=\text{900 kg}\end{align*}[/latex]
3. .
   1. .
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{{up}}}+{{F}_{g}}\\&=\text{200 + (15 x }-9.8)\\&=\text{53 N up}\end{align*}[/latex]
   2. .
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\\text{ 53}&= \text{15}a\\\text{ }a&=\text{3}\text{.53 m}\text{.}{{\text{s}}^{{-2}}}\text{ up}\end{align*}[/latex]
4. Let up be positive.
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{2 000 x 0}\text{.3}\\&=\text{600 N up}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{T}}+{{F}_{g}}\\\text{600}&={{F}_{T}}\text{ + (2 000 x }-9.8)\\\text{ }{{F}_{T}}&=\text{20 200 N up}\end{align*}[/latex]
5. .
   1. Let to the right be positive.
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{A}}+{{F}_{f}}\\&=\text{80 + (}-10)\\&=\text{70 N right}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\70&= 16a\\a&=4.38~\text{m.s}^{-2}~\text{ right}\end{align*}[/latex]
   2. For Q only:
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=8 \times 4.38\\&=35~\text{N}\end{align*}[/latex]
      [latex]\scriptsize \begin{align*}{{F}_{{net}}}&={{F}_{A}}+{{F}_{P}}\\35&=80+{{F}_{P}}\\{{F}_{P}}&=-45\\&=45~\text{N left}\end{align*}[/latex]
6. Let up be positive.
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{2 000 x 25}\\&=\text{500 000 N up }\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{{up}}}+{{F}_{g}}\\\text{500 000}&={{F}_{{up}}}\text{+ (20 000 x }-9.8)\\\text{ }{{F}_{{up}}}&=\text{696 000 N up}\end{align*}[/latex]
7. .
   1. When a net force is applied to an object of mass, the object accelerates in the direction of the net force. The acceleration is directly proportional to the net force and inversely proportional to the mass.
   2. .
      [latex]\scriptsize \begin{align*}{{F}_{{netB}}}&={{F}_{T}}+{{F}_{f}}\\\text{ }ma&=\text{600 + (}-200)\\\text{ 1 200}a&=\text{ 400}\\\text{ }a&=\text{0}\text{.33 m}\text{.}{{\text{s}}^{{-2}}}\text{ forward}\end{align*}[/latex]
   3. .
      [latex]\scriptsize \begin{align*}\text{ }{{F}_{{netA}}}&={{F}_{A}}+{{F}_{T}}+{{F}_{f}}\\\text{ }ma&={{F}_{A}}\text{+ (}-T)+(-200)\\\text{1 200 x 0}\text{.3 }&={{F}_{A}}-600-200\\\text{ }{{F}_{A}}&=1\text{ }200\text{ N forward}\end{align*}[/latex]
8. Let to the right be positive.
   For A:
   [latex]\scriptsize \begin{align*}{{F}_{{netB}}}&={{F}_{T}}+{{F}_{f}}\\\text{ }ma&=T\text{ + (}-5)\\\text{ 3}a\text{ }&=T-5...eqtn\text{ }1\end{align*}[/latex]
   For B:
   [latex]\scriptsize \begin{align*}{{F}_{{netB}}}&={{F}_{A}}+{{F}_{f}}+{{F}_{T}}\\\text{ }ma&=\text{28+(}-3)+(-T)\\\text{ 2}a\text{ }&=25-T...eqtn\text{ }2\end{align*}[/latex]
   Solve simultaneously:
   [latex]\scriptsize \begin{align*}3a+2a&=T-5+25\_T\\\text{ }5a&=20\\\text{ }a&=\text{4 m}\text{.}{{\text{s}}^{{-2}}}\text{ right}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\text{ }3a&=T-5\\3(4)&=T-5\\\text{ }T&=17\text{ N}\end{align*}[/latex]
9. Let down be positive.
   [latex]\scriptsize \begin{align*}{{F}_{{net}}}&=ma\\&=\text{240 x 1}\text{.5}\\&=\text{360 N down }\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{f}}+{{F}_{{x\text{ }of\text{ }g}}}\\\text{360}&=-49\text{+(240 x }9.8)\sin \theta \\\text{409 }&=2352\sin \theta \\\text{ }\sin \theta &=0.17\\\text{ }\theta &=\text{1}{{\text{0}}^{0}}\end{align*}[/latex]
10. Let down be positive.
    For the [latex]\scriptsize 500\text{ kg}[/latex] mass:
    [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{{T2}}}+{{F}_{g}}\\\text{ }ma&=-500\text{+(500 x 9}.8)\\\text{500}a&=4\text{ }400\\\text{ }a&=\text{8}\text{.8 m}\text{.}{{\text{s}}^{{-2}}}\text{ down}\end{align*}[/latex]
    For the [latex]\scriptsize 750\text{ kg}[/latex] mass:
    [latex]\scriptsize \begin{align*}\text{ }{{F}_{{net}}}&={{F}_{{T1}}}+{{F}_{{T2}}}+{{F}_{g}}\\\text{ }ma&={{F}_{{T1}}}\text{+500 +(750 x }-9.8)\\\text{750 x 8}\text{.8 }&=\text{ }T1\text{ + 7350}\\\text{ 6 600}&=T1\text{ + 7350}\\\text{ }T&=-750\text{ N}\\&=\text{750 N up}\end{align*}[/latex]

Back to Unit 2: Assessment