Chemical Change: Describe, analyse and apply quantitative aspects of change
Unit 2: The mole
Emma Harrage
Unit outcomes
By the end of this unit you will be able to:
- Define the mole.
- Calculate the molar volume of gases.
- Understand the volume relationships in gaseous reactions.
What you should know
Before you start this unit, make sure you can:
- Calculate atomic, molecular and formula mass. Refer to level 2 subject outcome 6.4 unit 1 to revise this.
Introduction
Parts of the text in this unit were sourced from Siyavula Physical Science Gr11 Learner’s Book, Chapter 8, released under a CC-BY licence.
The mole is a measure of the number of atoms, ions, or molecules in a substance. It is a fixed number with a value of [latex]\scriptsize \displaystyle 6.02214076\text{ x }{{10}^{{23}}}[/latex] which is referred to as Avogadro’s number or constant. Using the mole we can calculate the amount of a substance in grams and work out the molar volume of gases.
Atomic mass and the mole
As we learnt in level 2 the chemical equation for a reaction can provide us with useful information. It tells us what the reactants and the products are in the reaction, and it also tells us the ratio in which the reactants combine to form products. Look at the equation below:
[latex]\scriptsize \displaystyle \text{Mg + O}\to \text{MgO}[/latex]
In this reaction, every atom of magnesium (Mg) will react with a single atom of oxygen (O) to form magnesium oxide (MgO). However, what the equation does not tell us, is the quantities or the amount of each substance that is involved. It is important to know the quantities of reactants that are needed, and the quantity of product that will be formed.
Sometimes it is important to know exactly how many particles (e.g. atoms or molecules) are in a sample of a substance, or what quantity of a substance is needed for a chemical reaction to take place. The amount of substance is so important in chemistry that it is given its own name, which is the .
The mole (abbreviation ‘mol’) is the SI (Standard International) unit for ‘amount of substance’.
The mole is a counting unit just like hours or days. The mole is [latex]\scriptsize \displaystyle 602\text{ }204\text{ }500\text{ }000\text{ }000\text{ }000\text{ }000\text{ }000[/latex]or [latex]\scriptsize \displaystyle 6,022\times {{10}^{{23}}}[/latex] particles. We call this number .
If we had this number of cold drink cans, then we could cover the surface of the earth to a depth of over [latex]\scriptsize \displaystyle 300\text{ km}[/latex]!
We use Avogadro’s number and the mole in chemistry to help us quantify what happens in chemical reactions. If we measure [latex]\scriptsize \displaystyle 12.0\text{ g}[/latex] of carbon, we have one mole or [latex]\scriptsize \displaystyle 6,022\times {{10}^{{23}}}[/latex] carbon atoms. [latex]\scriptsize \displaystyle 63.5\text{ g}[/latex] of copper is one mole of copper or [latex]\scriptsize \displaystyle 6,022\times {{10}^{{23}}}[/latex] copper atoms. In fact, if we measure the of any element on the periodic table, we have one mole of that element.
Note
The number below the symbol for an element on the periodic table is its relative atomic mass.
For example, the relative atomic mass of iron is [latex]\scriptsize \displaystyle 55.85[/latex]:
[latex]\scriptsize \underset{{\text{55}\text{.85}}}{\overset{{\text{26}}}{\mathop {\text{Fe}}}}\,[/latex]
The mole
The mole is a unit for the amount of substance similar to familiar units such as grams or kilograms. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter.
A mole is defined as the amount of substance containing the same number of particles as the number of atoms in a sample of pure carbon-12.
The mole is a unit of measurement that defines quantity as a counted number. It is the value of Avogadro’s constant, which is [latex]\scriptsize \displaystyle 6,022\times {{10}^{{23}}}[/latex].
Note
Watch this video to understand how big a mole actually is: How big is a mole? (Not the animal, the other one.)
For example, Lithium (Li), with three protons and three neutrons in its nucleus, has half the atomic mass of carbon. The same number of atoms, each of which weighs half the mass of carbon, should produce a total mass of half of our [latex]\scriptsize 12[/latex] grams of carbon. That means that in [latex]\scriptsize \text{6g}[/latex] of Li, there are [latex]\scriptsize \displaystyle \text{6}\text{.022 x 1}{{\text{0}}^{{\text{23}}}}[/latex] Li atoms. It turns out that there are [latex]\scriptsize \displaystyle \text{6}\text{.022 x 1}{{\text{0}}^{{\text{23}}}}[/latex] atoms of any element in n grams of that element, where n is its relative atomic mass.
Take note!
Remember that there are [latex]\scriptsize \displaystyle \text{6}\text{.022 x 1}{{\text{0}}^{{\text{23}}}}[/latex] atoms of any element in a mass of that element equal to the relative atomic mass expressed in grams. That mass is called [latex]\scriptsize 1[/latex] mole of the element. Note, the symbol for mole is mol.
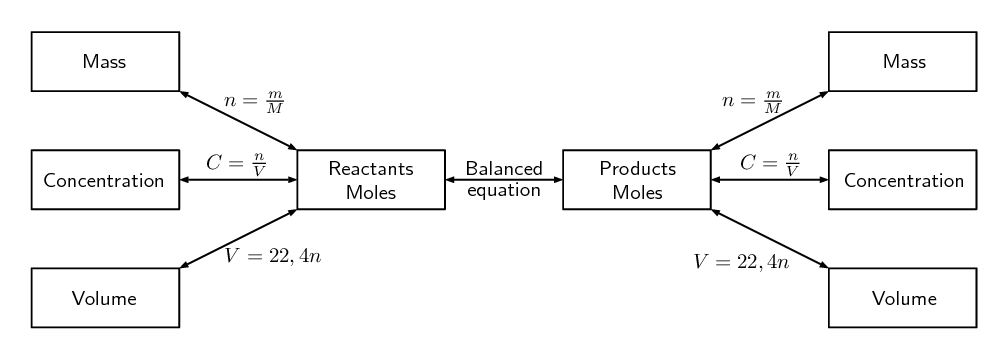
As we learnt in level 2 subject outcome 6.4 unit 1, the equation to calculate moles or molar mass or the mass of a substance is [latex]\scriptsize \text{n = }\displaystyle \frac{\text{m}}{\text{M}}[/latex]
Where:
M = molar mass of the pure substance (measured in [latex]\scriptsize \displaystyle g.mo{{l}^{{-1}}}[/latex])
m = mass of the pure substance (measured in grams, g)
n = amount of the pure substance (measured in moles, mol)
Exercise 2.1
- How many atoms are there in:
- [latex]\scriptsize \displaystyle 1[/latex] mole of a substance
- [latex]\scriptsize \displaystyle 2[/latex] moles of calcium
- [latex]\scriptsize \displaystyle 5[/latex] moles of phosphorus
- [latex]\scriptsize \displaystyle 24.3[/latex] g of magnesium
- [latex]\scriptsize \displaystyle 24.0[/latex] g of carbon
- Calculate the number of moles of carbon dioxide molecules in [latex]\scriptsize \displaystyle 22\text{ g}[/latex] of [latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex].
- Calculate the mass of [latex]\scriptsize \displaystyle 2[/latex] mol of [latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex].
The full solutions can be found at the end of the unit.
Molar volume of gases
It is rather tricky to find the number of moles of a gas by measuring its mass. Chemists determine the number of moles of any gas by measuring its volume. However, this cannot be done for solids and liquids.
It is found that under the same temperature and pressure, equal volumes of all gases contain the same number of particles. Therefore, chemists introduced the concept of .
The molar volume of a gas is defined as the volume of one mole of the gas. So, the molar volume is also the volume occupied by [latex]\scriptsize \displaystyle 6.02\text{ x }{{10}^{{23}}}[/latex] particles of gas.
The molar volume of any gas is [latex]\scriptsize \displaystyle 22.4\text{ d}{{\text{m}}^{\text{3}}}\text{.mo}{{\text{l}}^{{\text{-1}}}}[/latex] at .
STP refers to standard temperature of [latex]\scriptsize 273\text{ K}[/latex] and pressure of [latex]\scriptsize 101.3\text{ kPa}[/latex].
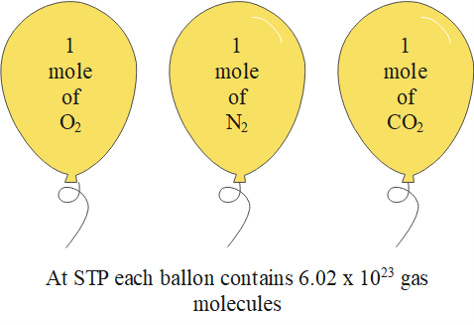
It is possible to calculate the volume of one mole of gas at STP using what we now know about gases.
We write down all the values that we know about one mole of gas at STP:
[latex]\scriptsize \displaystyle \begin{align*}p&=101.3\text{ kPa}=101\text{ }300\text{ Pa}\\n&=1\text{ mol}\\R&=8.31\text{ J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\T&=273\text{ K}\end{align*}[/latex]
Now we can substitute these values into the ideal gas equation:
[latex]\scriptsize \displaystyle \begin{align*}pV&=nRT\\\left( {101\text{ }300} \right)V&=\left( 1 \right)\left( {8.31} \right)\left( {273} \right)\\\left( {101\text{ }300} \right)V&=2\text{ }265.9\\V&=0.0224\text{ }{{\text{m}}^{\text{3}}}=22.4\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
The volume of [latex]\scriptsize 1[/latex] mole of gas at STP is [latex]\scriptsize \displaystyle 22,4\text{ d}{{\text{m}}^{\text{3}}}[/latex]. If we had any number of moles of gas, not just one mole, then we would get: [latex]\scriptsize \displaystyle Vg=22.4 ng[/latex].
Example 2.1
What is the volume of [latex]\scriptsize \displaystyle 2.3\text{ mol}[/latex] of hydrogen gas at STP?
Solution
Find the volume
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{g}}&=\left( {22.4} \right)ng\\{{V}_{g}}&=\left( {22.4} \right)\left( {2.3} \right)\\{{V}_{g}}&=51.52\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Reactions and gases
Some reactions take place between gases. For these reactions we can work out the volumes of the gases using the fact that volume is proportional to the number of moles.
We can use the following formula: [latex]\scriptsize \displaystyle {{\text{V}}_{\text{A}}}\text{= }\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}[/latex]
Where:
[latex]\scriptsize {{\text{V}}_{\text{A}}}[/latex] = volume of A
[latex]\scriptsize {{\text{V}}_{\text{B}}}[/latex] = volume of B
a = stoichiometric coefficient of A
b = stoichiometric coefficient of B
Note
The number in front of a reactant or a product in a balanced chemical equation is called the stoichiometric coefficient or stoichiometric ratio.
Example 2.2
Hydrogen and oxygen react to form water at STP according to the following equation:
[latex]\scriptsize \displaystyle \text{2}{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}\text{+}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}[/latex]
If [latex]\scriptsize \displaystyle \text{3 d}{{\text{m}}^{\text{3}}}[/latex] of oxygen is used, what volume of water is produced?
Solution
We use the equation given above to work out the volume of water produced:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{\text{A}}}&=\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=\displaystyle \frac{2}{1}{{\text{V}}_{{{{\text{O}}_{\text{2}}}}}}\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=\text{2}\left( \text{3} \right)\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=\text{6 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
We can interpret the chemical equation in the worked example above as [latex]\scriptsize \displaystyle \text{2}{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}\text{+}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}[/latex]:
[latex]\scriptsize \displaystyle 2[/latex] moles of hydrogen react with [latex]\scriptsize \displaystyle 1[/latex] mole of oxygen to produce [latex]\scriptsize \displaystyle 2[/latex] moles of water. We can also say that [latex]\scriptsize \displaystyle 2[/latex] volumes of hydrogen react with [latex]\scriptsize \displaystyle 1[/latex] volume of oxygen to produce [latex]\scriptsize \displaystyle 2[/latex] volumes of water.
Example 2.3
What volume of oxygen at STP is needed for the complete combustion of [latex]\scriptsize \displaystyle 3.3\text{ d}{{\text{m}}^{\text{3}}}[/latex] of propane ([latex]\scriptsize \displaystyle {{\text{C}}_{\text{3}}}{{\text{H}}_{\text{8}}}[/latex])?
Hint: [latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex] and [latex]\scriptsize \displaystyle {{\text{H}}_{\text{2}}}\text{O}[/latex] are the products as in all combustion reactions.
Solution
Step 1: Write a balanced equation for the reaction
[latex]\scriptsize \displaystyle {{\text{C}}_{\text{3}}}{{\text{H}}_{{\text{8}\left( \text{g} \right)}}}\text{+5}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{3C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\text{+ 4}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}[/latex]
Step 2: Determine the volume of oxygen needed for the reaction
We use the equation given above to work out the volume of oxygen needed:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{\text{A}}}&=\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}\\{{\text{V}}_{{{{\text{O}}_{\text{2}}}}}}&=\displaystyle \frac{5}{1}{{\text{V}}_{{{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{8}}}}}}\\{{\text{V}}_{{{{\text{O}}_{\text{2}}}}}}&=\text{5}\left( {\text{3}\text{.3}} \right)\\{{\text{V}}_{{{{\text{O}}_{\text{2}}}}}}&=\text{16}\text{.5 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Exercise 2.2
Methane burns in oxygen at STP, forming water and carbon dioxide according to the following equation:
[latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{{\text{4}\left( \text{g} \right)}}}\text{+2}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
If [latex]\scriptsize \displaystyle 4\text{ d}{{\text{m}}^{\text{3}}}[/latex] of methane is used, what volume of water is produced?
The full solutions can be found at the end of the unit.
Volume relationships in gaseous reactions
In unit 1 we learnt to balance chemical equations and in subject outcome 5.4 we learnt about the different gas laws. We can now apply these principles to reactions involving gases.
Example 2.4
Ammonium nitrate is used as an explosive in mining. The following reaction occurs when ammonium nitrate is heated:
[latex]\scriptsize \displaystyle \text{2N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{{\text{3}\left( \text{s} \right)}}}\text{ }\to \text{2}{{\text{N}}_{{\text{2}\left( \text{g} \right)}}}\text{ + 4}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}\text{+ }{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
If [latex]\scriptsize \displaystyle 750\text{ g}[/latex] of ammonium nitrate is used, what volume of oxygen gas would we expect to produce at STP?
Solution
Step 1: Work out the number of moles of ammonium nitrate
[latex]\scriptsize _{M}\text{(N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}\text{)}=(14+4+14+48)=80[/latex]
[latex]\scriptsize \displaystyle \begin{align*}n&=\displaystyle \frac{m}{M}\\n&=\displaystyle \frac{{750}}{{80}}=9.375\text{ mol}\end{align*}[/latex]
Step 2: Work out the amount of oxygen
The mole ratio of [latex]\scriptsize \displaystyle \text{N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}[/latex] to [latex]\scriptsize \displaystyle {{\text{O}}_{\text{2}}}[/latex] is [latex]\scriptsize \displaystyle 2:1[/latex]. The stoichiometric coefficient for ammonia is [latex]\scriptsize \displaystyle 2[/latex] and for oxygen it is [latex]\scriptsize \displaystyle 1[/latex].
So the number of moles of [latex]\scriptsize \displaystyle {{\text{O}}_{\text{2}}}[/latex] is:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{n}}_{{{{\text{O}}_{\text{2}}}}}}&={{\text{n}}_{{\text{N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{stoichiometric coefficient }{{\text{O}}_{\text{2}}}}}{{\text{stoichiometric coefficient N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}}}\\ &=\text{9}\text{.375 mol N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{1 mol }{{\text{O}}_{\text{2}}}}}{{\text{2 mol N}{{\text{H}}_{\text{4}}}\text{N}{{\text{O}}_{\text{3}}}}}\\ &=\text{4}\text{.6875 mol}\end{align*}[/latex]
Step 3: Work out the volume of oxygen
Remember that one mole of any gas occupies [latex]\scriptsize \displaystyle 22.4\text{ d}{{\text{m}}^{\text{3}}}[/latex] at STP.
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=\left( {\text{22}\text{.4}} \right)\\\text{n}&=\left( {\text{22}\text{.4}} \right)\left( {\text{4}\text{.6875}} \right)\text{=105 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Example 2.5
Airbags in cars use a controlled explosion to inflate the bag. When a car hits another car or an object, various sensors trigger the airbag. A chemical reaction then produces a large volume of gas which inflates the airbag.
Sodium azide is sometimes used in airbags. When triggered, it has the following reaction:
[latex]\scriptsize \displaystyle \text{2Na}{{\text{N}}_{{\text{3}\left( \text{s} \right)}}}\to \text{2N}{{\text{a}}_{{\left( \text{s} \right)}}}\text{+3}{{\text{N}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
If [latex]\scriptsize \displaystyle 55[/latex] grams of sodium azide is used, what volume of nitrogen gas would we expect to produce?
Solution
Step 1: Work out the number of moles of sodium azide
[latex]\scriptsize _{\text{M}}\text{(Na}{{\text{N}}_{\text{3}}}\text{) = (23+42) = 65}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}\text{n}&=\displaystyle \frac{\text{m}}{\text{M}}\\\text{n}&=\displaystyle \frac{{\text{55}}}{{\text{65}}}\text{= 0}\text{.85 mol}\end{align*}[/latex]
Step 2: Work out the amount of nitrogen
The mole ratio of [latex]\scriptsize \displaystyle \text{Na}{{\text{N}}_{\text{3}}}[/latex] to [latex]\scriptsize \displaystyle {{\text{N}}_{\text{2}}}[/latex] is [latex]\scriptsize \displaystyle 2:3[/latex]. So the number of moles of is [latex]\scriptsize \displaystyle {{\text{N}}_{\text{2}}}[/latex]:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{n}}_{{{{\text{N}}_{\text{2}}}}}}&={{\text{n}}_{{\text{Na}{{\text{N}}_{\text{3}}}}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{stoichiometric coefficient }{{\text{N}}_{\text{2}}}}}{{\text{stoichiometric coefficient Na}{{\text{N}}_{\text{3}}}}}\\&=\text{0}\text{.85 molNa}{{\text{N}}_{\text{3}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{3 mol }{{\text{N}}_{\text{2}}}}}{{\text{2 mol Na}{{\text{N}}_{\text{3}}}}}\\ &=\text{1}\text{.27 mol }{{\text{N}}_{\text{2}}}\end{align*}[/latex]
Step 3: Work out the volume of nitrogen
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=\left( {\text{22}\text{.4}} \right)\\\text{n}&=\left( {\text{22}\text{.4}} \right)\left( {\text{1}\text{.27}} \right)\text{= 28}\text{.4 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Exercise 2.3
- What volume of oxygen is needed for the complete combustion of [latex]\scriptsize \displaystyle 5\text{ g}[/latex] of magnesium to form magnesium oxide?
- Annalise is making a mini volcano for her science project. She mixes baking soda which is mostly [latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{\text{3}}}[/latex] and vinegar (acetic acid) which is mostly [latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{\text{3}}}\text{COOH}[/latex] together to make her volcano erupt. The reaction for this equation is:
[latex]\scriptsize \displaystyle \text{NaHC}{{\text{O}}_{{\text{3}\left( \text{s} \right)}}}\text{+ C}{{\text{H}}_{\text{3}}}\text{COO}{{\text{H}}_{{\left( {\text{aq}} \right)}}}\to \text{C}{{\text{H}}_{\text{3}}}\text{COON}{{\text{a}}_{{\left( {\text{aq}} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{l} \right)}}}\text{+C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
.
What volume of carbon dioxide is produced if Annalise uses [latex]\scriptsize \displaystyle 50[/latex] ml of [latex]\scriptsize \displaystyle 0.2\text{ mol}\text{.d}{{\text{m}}^{\text{3}}}[/latex] acetic acid?
The full solutions can be found at the end of the unit.
Summary
In this unit you have learnt the following:
- The volume of one mole of gas at STP is [latex]\scriptsize \displaystyle 22.4\text{ d}{{\text{m}}^{\text{3}}}[/latex].
- For any number of moles of gas at STP we can use [latex]\scriptsize \displaystyle {{\text{V}}_{\text{g}}}\text{ =22}\text{.4ng}[/latex] to find the volume.
- The volume relationship for two gases in a reaction is given by: [latex]\scriptsize \displaystyle {{\text{V}}_{\text{A}}}\text{= }\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}[/latex], where [latex]\scriptsize {{\text{V}}_{\text{A}}}[/latex] is the volume of gas A, [latex]\scriptsize {{\text{V}}_{\text{B}}}[/latex] is the volume of gas B, a is the stoichiometric coefficient of gas A and b is the stoichiometric coefficient of gas B.
- The molar volume of a gas expresses the volume occupied by [latex]\scriptsize \displaystyle 1[/latex] mole of that respective gas under certain temperature and pressure conditions.
- The most common example is the molar volume of a gas at STP which is equal to [latex]\scriptsize \displaystyle 22.4\text{ d}{{\text{m}}^{\text{3}}}[/latex] for [latex]\scriptsize 1[/latex] mole of any ideal gas at a temperature equal to [latex]\scriptsize \displaystyle 273\text{ K}[/latex] and a pressure equal to [latex]\scriptsize \displaystyle 1.00[/latex] atm.
Unit 2: Assessment
Suggested time to complete: 20 minutes
- Acetylene ([latex]\scriptsize \displaystyle {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{2}}}[/latex]) burns in oxygen according to the following reaction:
[latex]\scriptsize \displaystyle \text{2}{{\text{C}}_{\text{2}}}{{\text{H}}_{{\text{2}\left( \text{g} \right)}}}\text{+5}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{4C}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\text{+2}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}[/latex]
.
If [latex]\scriptsize \displaystyle 3.5\text{ d}{{\text{m}}^{\text{3}}}[/latex] of acetylene gas is burnt, what volume of carbon dioxide will be produced? - Given the following reaction:
[latex]\scriptsize \displaystyle \text{3N}{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\text{+}{{\text{H}}_{\text{2}}}{{\text{O}}_{{\left( \text{g} \right)}}}\to \text{2HN}{{\text{O}}_{{\text{3}\left( \text{g} \right)}}}\text{+ N}{{\text{O}}_{{\left( \text{g} \right)}}}[/latex]
.
If [latex]\scriptsize \displaystyle \text{2}\text{.7 d}{{\text{m}}^{\text{3}}}[/latex] of [latex]\scriptsize \displaystyle \text{N} {{\text{O}}_{\text{2}}}[/latex] is used, what volume of [latex]\scriptsize \displaystyle \text{HN}{{\text{O}}_{\text{3}}}[/latex] is produced?
.
[latex]\scriptsize \displaystyle \begin{align*}&\text{a}\text{. 4}\text{.1 d}{{\text{m}}^{\text{3}}} \\ &{\text{b}\text{. 2}\text{.7 d}{{\text{m}}^{\text{3}}}} \\ &{\text{c}\text{. 1}\text{.8 d}{{\text{m}}^{\text{3}}}} \\ &{\text{d}\text{. 3}\text{.4 d}{{\text{m}}^{\text{3}}}} \end{align*}[/latex] - Some airbags contain a mixture of sodium azide ([latex]\scriptsize \displaystyle \text{Na}{{\text{N}}_{\text{3}}}[/latex]) and potassium nitrate ([latex]\scriptsize \displaystyle \text{KN}{{\text{O}}_{\text{3}}}[/latex]). When a car crash is detected by the signalling system, the sodium azide is heated until it decomposes to form nitrogen gas and sodium metal: [latex]\scriptsize \displaystyle \text{2Na}{{\text{N}}_{{\text{3}\left( \text{s} \right)}}}\to \text{2N}{{\text{a}}_{{\left( \text{s} \right)}}}\text{+3}{{\text{N}}_{{\text{2}\left( \text{g} \right)}}}[/latex].
.
The potassium nitrate then reacts with the sodium metal forming more nitrogen:
[latex]\scriptsize \displaystyle \text{10N}{{\text{a}}_{{\left( \text{s} \right)}}}\text{+2KN}{{\text{O}}_{{\text{3}\left( \text{s} \right)}}}\to {{\text{K}}_{\text{2}}}{{\text{O}}_{{\left( \text{s} \right)}}}\text{+5N}{{\text{a}}_{\text{2}}}{{\text{O}}_{{\left( \text{s} \right)}}}\text{+ }{{\text{N}}_{{\text{2}\left( \text{g} \right)}}}[/latex]
.
A typical passenger side airbag contains [latex]\scriptsize \displaystyle 250\text{ g}[/latex] of sodium azide.- What mass of sodium metal is formed in the first reaction?
- What is the total volume of nitrogen gas formed from both reactions?
The full solutions can be found at the end of the unit.
Unit 2: Solutions
Exercise 2.1
- .
- .
[latex]\scriptsize \displaystyle 1 \text{ mole of a substance contains } \text{6 x 1}{{\text{0}}^{{\text{23}}}}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*} 2 \text{ moles of calcium}&= \text{2 x 6}\text{.02 x 1}{{\text{0}}^{{\text{23}}}}\\&=\text{1}\text{.204 x 1}{{\text{0}}^{{\text{24}}}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*} 5 \text{ moles of phosphorus}&= \text{5 x 6}\text{.02 x 1}{{\text{0}}^{{\text{23}}}}\\&=\text{3}\text{.01 x 1}{{\text{0}}^{{\text{24}}}}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle 24.3 \text{ g of magnesium}= \text{1 x 6}\text{.02 x 1}{{\text{0}}^{{\text{23}}}}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*} 24.0 \text{ g of carbon}&= \text{2 x 6}\text{.02 x 1}{{\text{0}}^{{\text{23}}}}\\&=\text{1}\text{.204 x 1}{{\text{0}}^{{\text{24}}}}\end{align*}[/latex]
- .
- Relative atomic mass:
[latex]\scriptsize \displaystyle \begin{align*}\text{C}&=12\\\text{O}&=16\end{align*}[/latex]
.
Molar mass of carbon dioxide:
[latex]\scriptsize \displaystyle 12\text{ }+\text{ }16\text{ }+\text{ }16\text{ }=\text{ }44\text{ g}\text{.mo}{{\text{l}}^{{-1}}}[/latex]
.
Number of moles:
[latex]\scriptsize \displaystyle \begin{align*}\text{n}&=\displaystyle \frac{\text{m}}{\text{M}}\\&=\text{ }\displaystyle \frac{{22}}{{44}}=\text{ }0.5\text{ mol}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}\text{m}&= \text{n x M}\\\text{m}&=\text{ }2\text{ }\times \text{ }44\text{ }\\\text{m}&=88\text{ g}\end{align*}[/latex]
Exercise 2.2
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{\text{A}}}&=\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=12{{\text{V}}_{{\text{C}{{\text{H}}_{4}}}}}\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=12(4)\\{{\text{V}}_{{{{\text{H}}_{\text{2}}}\text{O}}}}&=8~\text{d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Exercise 2.3
- The balanced equation for this reaction is:
[latex]\scriptsize \displaystyle \text{2M}{{\text{g}}_{{\left( \text{s} \right)}}}\text{+ }{{\text{O}}_{{\text{2}\left( \text{g} \right)}}}\to \text{2Mg}{{\text{O}}_{{\left( \text{s} \right)}}}[/latex]
.
The number of moles of magnesium used is:
[latex]\scriptsize \displaystyle \begin{align*}\text{n}&= \displaystyle \frac{\text{m}}{\text{M}}\\\text{n}&=\displaystyle \frac{5}{{24}}\text{= 0}\text{.2083 mol}\end{align*}[/latex]
.
The mole ratio of Mg to [latex]\scriptsize \displaystyle {{\text{O}}_{\text{2}}}[/latex] is [latex]\scriptsize \displaystyle 2:1[/latex]. So the number of moles of is [latex]\scriptsize \displaystyle {{\text{O}}_{\text{2}}}[/latex]:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{n}}_{{{{\text{O}}_{\text{2}}}}}}&={{\text{n}}_{{\text{Mg}}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{stoichiometric coefficient O2}}}{{\text{stoichiometric coefficient Mg}}}\\&=\text{0}\text{.2083 mol Mg }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{ 1mol }{{\text{O}}_{\text{2}}}}}{{\text{2 mol Mg}}}\\&=\text{0}\text{.1042 mol }{{\text{O}}_{\text{2}}}\end{align*}[/latex]
.
The volume of oxygen is:
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=\left( {\text{22}\text{.4}} \right)\\\text{n}&=\left( {\text{22}\text{.4}} \right)\left( {\text{0}\text{.1042}} \right)\text{ = 2}\text{.33 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex] - The number of moles of acetic acid used is:
[latex]\scriptsize \displaystyle \begin{align*}\text{C}&=\displaystyle \frac{\text{n}}{\text{V}}\\0.2&=\displaystyle \frac{\text{n}}{{\text{0}\text{.05}}}\\\text{n}&= \text{0}\text{.01 mol}\end{align*}[/latex]
.
The mole ratio of [latex]\scriptsize \displaystyle \text{C}{{\text{H}}_{\text{3}}}\text{COOH}[/latex] to [latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex] is [latex]\scriptsize \displaystyle 1:1[/latex]. So the number of moles of [latex]\scriptsize \displaystyle \text{C}{{\text{O}}_{\text{2}}}[/latex] is [latex]\scriptsize \displaystyle \text{0}\text{.01 mol}[/latex].
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=\left( {\text{22}\text{.4}} \right)\\\text{n}&=\left( {\text{22}\text{.4}} \right)\left( {\text{0}\text{.01}} \right)\\\text{n }&= \text{ 0}\text{.224 d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Unit 2: Assessment
- .
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{\text{A}}}&=\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}\\{{\text{V}}_{{\text{C}{{\text{O}}_{\text{2}}}}}}&=42(3.5)\\{{\text{V}}_{{\text{C}{{\text{O}}_{\text{2}}}}}}&=7~\text{d}{{\text{m}}^{\text{3}}}\end{align*}[/latex] - c)
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{\text{A}}}&=\displaystyle \frac{\text{a}}{\text{b}}{{\text{V}}_{\text{B}}}\\{{\text{V}}_{{\text{HN}{{\text{O}}_{\text{3}}}}}}&=\displaystyle \frac{2}{3}{{\text{V}}_{{\text{N}{{\text{O}}_{\text{2}}}}}}\\{{\text{V}}_{{\text{HN}{{\text{O}}_{\text{3}}}}}}&=\displaystyle \frac{2}{3}\text{(2}\text{.7)}\\{{\text{V}}_{{\text{HN}{{\text{O}}_{\text{3}}}}}}&=\text{1}\text{.8 }\!\!~\!\!\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex] - .
- The amount of sodium metal:
[latex]\scriptsize \displaystyle \text{n}=\displaystyle \frac{{250}}{{65}}=3.846~\text{mol}[/latex]
.
The molar ratio of sodium azide to sodium is [latex]\scriptsize \displaystyle 2:2\text{ }\left( {1:1} \right)[/latex] so the number of moles of sodium is: [latex]\scriptsize \displaystyle 3.846\text{ mol}[/latex]
.
And the mass of sodium metal is:
[latex]\scriptsize \displaystyle \begin{align*}\text{m}&= \text{ nM}\\\text{m}&=\left( {3.846} \right)\left( {23} \right)=88.461\text{ g}\end{align*}[/latex] - To find the total volume of nitrogen produced we need to calculate the volume of nitrogen produced in each reaction and then add these two numbers together.
.
The first reaction uses [latex]\scriptsize \displaystyle 3.846\text{ mol}[/latex] of sodium azide. The mole ratio of sodium azide to nitrogen is [latex]\scriptsize \displaystyle 2:3[/latex], so the number of moles of nitrogen is:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{n}}_{{{{\text{N}}_{\text{2}}}}}}&={{\text{n}}_{{\text{Na}}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{stoichiometric coefficient }{{\text{N}}_{\text{2}}}}}{{\text{stoichiometric coefficient Na}{{\text{N}}_{3}}}}\\&=\text{3}\text{.846 mol Na}{{\text{N}}_{3}}\text{ x }\displaystyle \frac{{\text{2 mol }{{\text{N}}_{\text{2}}}}}{{\text{3 mol Na}{{\text{N}}_{3}}}}\text{ =2}\text{.564 mol }{{\text{N}}_{\text{2}}}\end{align*}[/latex]
.
Now we find the volume:
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=22.4\\\text{n}&=\left( {22.4} \right)\left( {2.564} \right)=57.436\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
.
For the second reaction we have [latex]\scriptsize \displaystyle 3.846\text{ mol}[/latex] of sodium (the sodium from the first reaction is used up in the second reaction). The mole ratio of sodium to nitrogen is [latex]\scriptsize \displaystyle 10:1[/latex], so the number of moles of nitrogen is:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{n}}_{{{{\text{N}}_{\text{2}}}}}}&={{\text{n}}_{{\text{Na}}}}\text{ }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{stoichiometric coefficient }{{\text{N}}_{\text{2}}}}}{{\text{stoichiometric coefficient Na}}}\\&=\text{3}\text{.846 mol Na }\!\!\times\!\!\text{ }\displaystyle \frac{{\text{1 mol}{{\text{N}}_{\text{2}}}}}{{\text{10 mol Na}}}\\&=\text{0}\text{.385 mol }{{\text{N}}_{\text{2}}}\end{align*}[/latex]
.
Now we find the volume:
[latex]\scriptsize \displaystyle \begin{align*}\text{V}&=22,4\\\text{n}&=\left( {22.4} \right)\left( {0.385} \right)\\\text{n}&=8.615\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
.
And the total volume of nitrogen is:
[latex]\scriptsize \displaystyle \begin{align*}{{\text{V}}_{{\text{Total}}}}&={{\text{V}}_{\text{1}}}\text{+}{{\text{V}}_{\text{2}}}\\{{\text{V}}_{{\text{Total}}}}&=57.436+8.615\\{{\text{V}}_{{\text{Total}}}}&=66.051\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
- The amount of sodium metal:
Media Attributions
- Fig 1 © DHET is licensed under a CC BY (Attribution) license
- Fig 2 © Siyavula is licensed under a CC BY-ND (Attribution NoDerivatives) license
the relative molecular mass of a substance expressed in grams, the basic unit of amount of substance
the number of atoms or molecules in one mole of a substance, equal to 6.023 x 10^23; also called Avogadro’s constant
the average mass of an atom, compared to 1/12 the mass of a carbon-12 atom
the volume of one mole of a substance at a specified pressure and temperature
Standard temperature and pressure: a temperature of 273 K and a pressure of 101.3 kPa
