Unit outcomes

By the end of this unit you will be able to:

• Explain properties of a solid in terms of:
  • tensile strength
  • elasticity
  • fracture
  • creep
  • plasticity
  • ductility
  • brittleness.
• Explain and understand the difference between:
  • stress and strain
  • compression stress and shear stress.
• Define and explain Hooke’s law.

What you should know

Before you start this unit, make sure you can:

• Identify and describe the phases of matter (physical property of matter).
• Distinguish between the phases of matter in terms of energy, shape and volume.
• Classify and describe materials using observation and research according to macroscopic properties.

Refer to level 2 subject outcome 5.1 units 1 and 2 if you need help with these concepts.

Introduction

If you are reading this on a computer device such as a phone or a laptop, what materials is the device made of? Why do you think these materials were chosen? If you have a mobile phone, does it have a protective cover? What material is this cover made of? Why do you think this material was chosen? What would happen if you dropped your device?

If you are reading this on a piece of paper, what properties does paper have that makes it so well suited for making books?

What are you sitting on? What is this object made of? Why do you think these materials were chosen? Do the materials used make this seat comfortable? Why or why not?

Now, have a look around the room you are in right now. It probably has walls and a ceiling. What are the walls made of? What is the ceiling made of? Do you feel safe in the room, or do you worry that the structure is going to collapse on you?

Every object around us that has been made by people is made out of one or more specific materials. Every kind of material has specific properties, and it is these properties that make certain materials useful for certain objects. Would you make a needle out of rubber? Would you build a house out of paper? Would you create a phone out of concrete?

In this unit we are going to learn about the physical or mechanical properties of solids. We are going to learn how these properties are described and measured, and why some materials are better suited for different applications than others.

Elastic and non-elastic materials

What comes to mind when you read the words ‘elastic’ and ‘elasticity’? Like most people, you probably think of elastic bands. Elastic bands are certainly elastic. If you stretch them and then let go, they spring back into their original shape (see figure 1).

Speaking of things springing back into shape, springs are also elastic. If you stretch a spring, it literally springs back into shape (see figure 2). But springs are often made of steel, not a material one immediately associates with elasticity. But think about it. Take a kitchen knife and bend it sideways. What happens? It immediately snaps back into shape.

Now, can you think of any materials that are non-elastic? If you deform them, they do not snap back into their original shape. You may have thought of modelling clay or mud (see figure 3). If you deform or change the shape of these materials, they stay in the new shape. Imagine trying to model something out of clay and it keeps reverting to its original shape!

We can define elasticity as the property of a material that makes it regain its original shape once a deforming force has been removed. This means that even materials such as bone are elastic. If you pick up a heavy object, your bones deform slightly because of the mass. But as soon as you put the object down, they regain their original shape.

It does not matter how small the deformation is. In the case of bone, the deformations are tiny, but they are there.

However, if the deforming force is great enough, your bones can break. If you stretch a steel spring beyond a certain point, the spring becomes permanently deformed. If you stretch an elastic band too much, it breaks. All materials have their limit. So long as the deforming force is below this limit, they will regain their original shape. But as soon as the deforming force is greater than their elastic limit, they break, snap, or become permanently deformed (see figure 4).

All materials exhibit some form of elasticity. Those materials that have a large elastic limit are on the highly elastic side of the spectrum. Those materials that have a low elastic limit are on the less elastic/non-elastic side of the spectrum (see figure 5).

We sometimes use the term plastic to describe non-elastic materials.

Take note!

The measure of a material’s elasticity does not depend on how much the material deforms when a certain deforming force is applied to it. What matters is the magnitude of the deforming force it can withstand and still regain its original shape.

Therefore, the fact that, under a certain deforming force, a rubber wire will stretch more than a steel wire does not mean that rubber is more elastic than steel. In fact, steel is more elastic because it can withstand a greater deforming force before it is permanently deformed.

Take note!

Highly elastic materials are those that regain their original shape immediately and completely after the removal of a deforming force e.g., quartz and phosphor bronze, etc.
Highly plastic materials are those which do not regain their original configuration at all on the removal of a deforming force e.g., putty, paraffin, wax, etc.

Measuring elasticity

Now that we understand what we mean by elasticity, we need to find a way to measure the elasticity of different materials so that we can compare them.

Activity 1.1: Measure elastic bands

Time required: 60 minutes

What you need:

• a piece of paper
• a pen or pencil
• five identical elastic bands
• six paper clips
• five small plastic bags with [latex]\scriptsize 100\ \text{g}[/latex] of sugar in each
• a ruler
• a calculator

What to do:

1. Start by measuring the length of the elastic bands. They should all be the same length and thickness. Make a note of this length.
2. Take two paper clips and bend the inner loop out to create a double loop (see figure 6).
   

   

3. Hang the larger loop over a door handle, towel rail or any other firm support. Hang one of the elastic bands on the smaller loop.
4. Bend another paper clip in the same way and use it to connect a packet of sugar to the other end of the elastic band. Allow the bag to hang freely.
5. Measure and note the length of the elastic band now. Calculate the change in length (subtract the new length from the original length) of the elastic band. We call this [latex]\scriptsize \Delta L[/latex].
6. Connect another bag of sugar to the elastic band and let both bags hang freely. Measure and note the change in length ([latex]\scriptsize \Delta L[/latex]) of the elastic band again.
7. Suspend the other three bags in turn and measure and note the change in length of the elastic band after adding each one.
8. Create a plot of the data you have collected so far. Place the total mass suspended from the elastic band on the x-axis and the change in length of the elastic band on the y-axis. Once all your data points are plotted, draw a straight line that goes through or as close to as many points as possible.
9. Remove the bags of sugar.
10. Connect all five of the elastic bands to the same paper clip loop.
11. Once again, add each bag in turn and measure and note the change in length of the five elastic bands after adding each bag.
12. Remove the bags and, on the same axes as before, create a new plot of this data. Draw a new straight line that goes through or as close to as many points as possible. What do you notice about this new graph? How is it the same as the first graph? How does it differ from the first graph? Why do you think the graphs are different?
13. String the five elastic bands together end-to-end using the remaining paper clips.
14. Now, add each bag of sugar in turn to the end of the elastic band string and measure and note the change in length of each band and the entire string.
15. Remove the bags and, on the same axes as before, create a new plot of this data. What do you notice about this new graph? How is it the same as the first two graphs? How does it differ from the first two graphs? Why do you think the graphs are different?

What did you find?

Starting with the one elastic band, each time you added a bag of sugar to the elastic band, you stretched it some more. Each time you added another bag of sugar, you increased the deforming force on the elastic band.

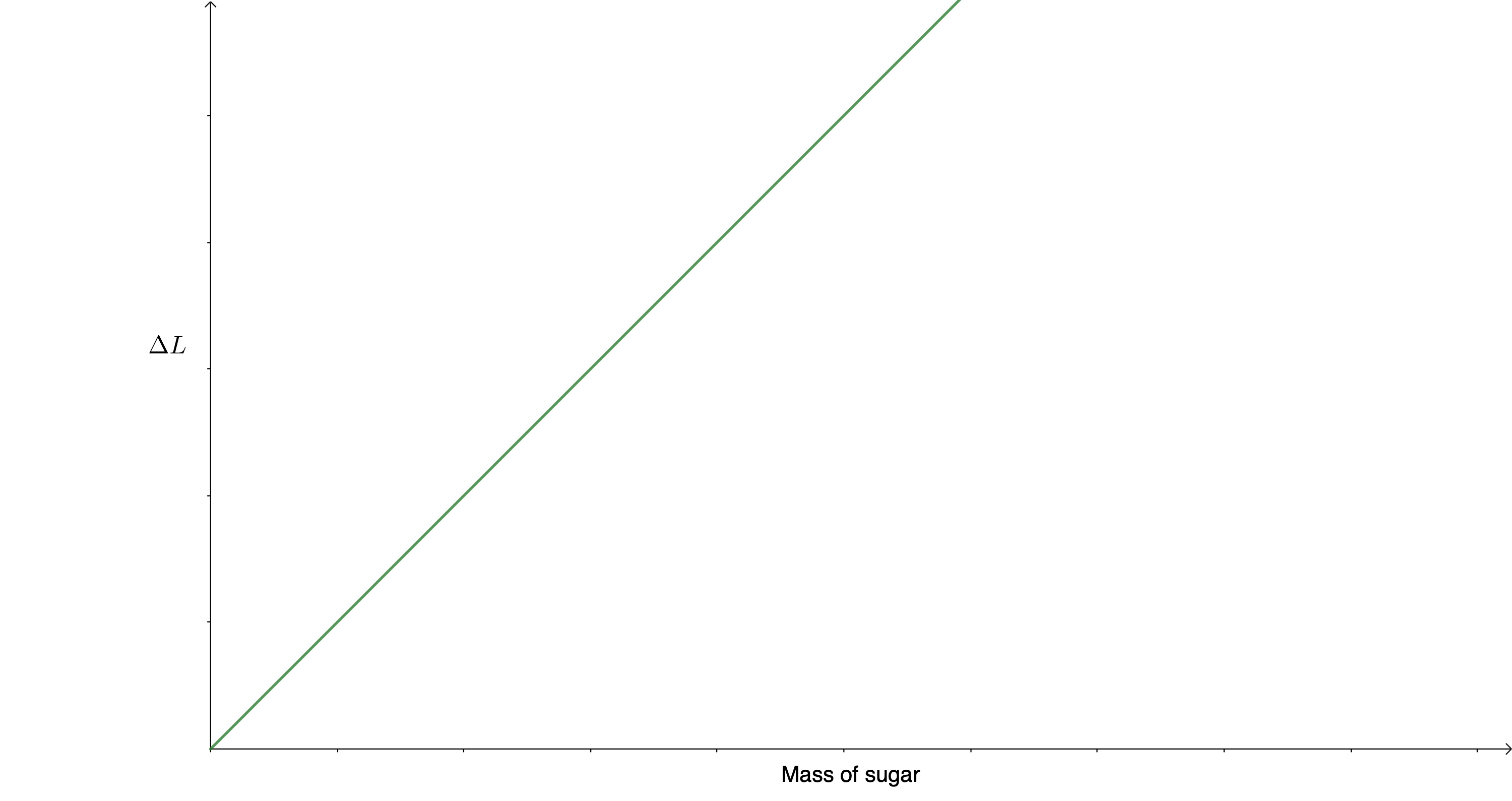
When adding bags of sugar in turn to a single elastic band, you should have seen that the change in the length of the elastic band was the same each time another bag was added. When you graph the change in length against the total mass of sugar, you should have gotten a straight line. This means that the change in length of the elastic band is proportional to the deforming force (the total mass of the sugar multiplied by the force due to gravity).

Your graph should have looked similar to figure 7. The exact change in length would have depended on the elastic band you were using.

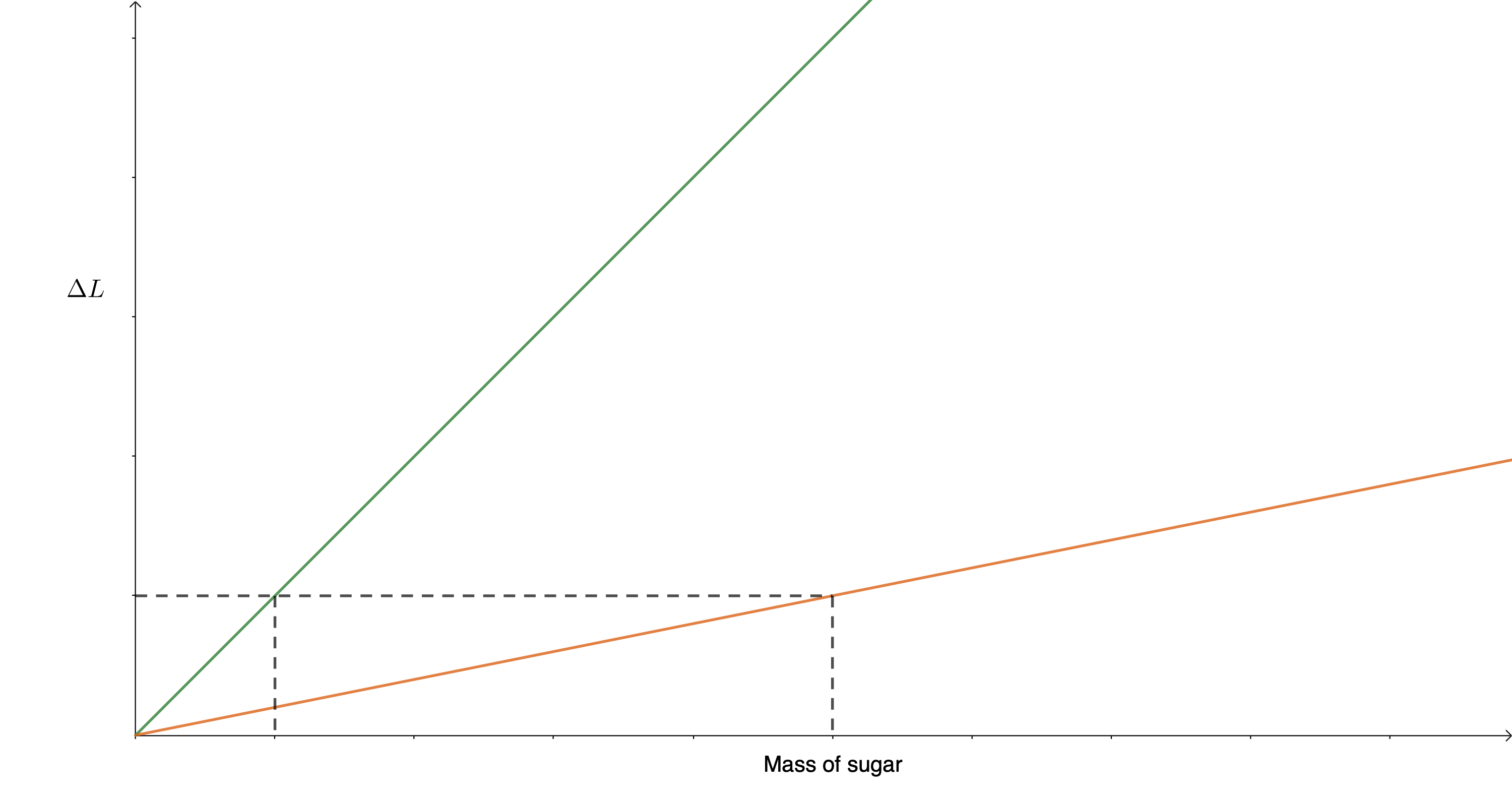
When you did the same experiment but with the five elastic bands connected to the same hook you basically created a single elastic band that was the same length but five times thicker than a single elastic band. In this case, when you plotted your data, you should have noticed that the change in the length of this ‘thicker’ elastic band was still proportional to the mass of sugar. However, because the new elastic band was five times thicker than the original, the change in length resulting from each additional bag of sugar was five times less. It took five times the original force to stetch the thicker elastic band the same amount as the original single elastic band (see figure 8). In figure 8, we can see that five times more sugar was needed to stretch the five-times thicker elastic band the same amount as the single elastic band.

When you strung the five elastic bands end-to-end you created an elastic band that was five times longer than the original but the same thickness. In this case, when you plotted your data, you should have found that this five-times longer elastic band stretched five times more for the same mass of sugar as a single elastic band (see figure 9).

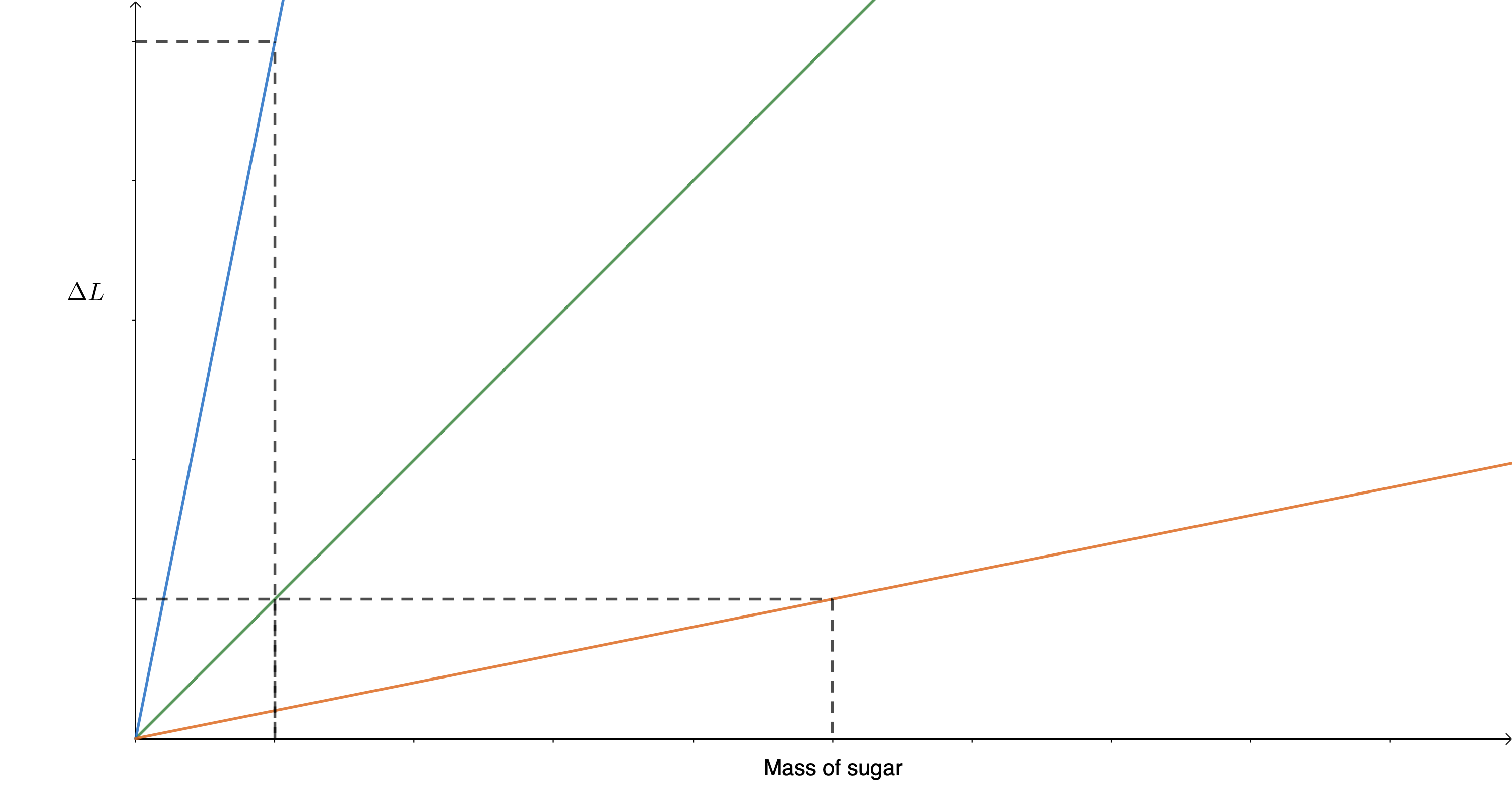
Another way to think of this is that each elastic band in the string still stretched the same amount as the original but when this change in length of all five elastic bands was added together, the sum of these changes was five times as great.

Let’s unpack and formalise what we discovered from activity 1.1 in a little more detail.

Stress

When we hang bags of sugar off the end of an elastic band the weight of the sugar pulls down and applies a deforming force to the elastic band which stretches it. We know that if we remove this downward force, the elastic band snaps back into its original shape. We call the deforming force on the elastic band, the load.

We can say that the load is proportional to the change in length [latex]\scriptsize \Delta L[/latex] of the elastic band. The greater the load applied, the greater the change in the length of the elastic band.

When we group five elastic bands together to form a single thicker elastic band, we see that the load needed to change the length of this thicker elastic band by the same amount as a single band is five times greater. This is precisely because the new elastic band is thicker. Another way of looking at this is that the thicker elastic band has a cross-sectional area five times greater than the original elastic band.

If the load required to stretch a single elastic band with a cross-sectional area of [latex]\scriptsize 10\ \text{m}{{\text{m}}^{\text{2}}}[/latex] by [latex]\scriptsize 1\ \text{cm}[/latex] is [latex]\scriptsize 100\ \text{N}[/latex], then the load needed to stretch an identical elastic band five times thicker (i.e. with a cross sectional area of [latex]\scriptsize 50\ \text{m}{{\text{m}}^{\text{2}}}[/latex]) by the same [latex]\scriptsize 1\ \text{cm}[/latex] will be [latex]\scriptsize 5\times 100\ \text{N}=500\ \text{N}[/latex]. Even though the load needed to stretch the thicker band by the same amount is greater, the load per unit of cross-sectional area is the same.

[latex]\scriptsize \displaystyle \frac{{100\ \text{N}}}{{10\ \text{m}{{\text{m}}^{\text{2}}}}}=\displaystyle \frac{{500\ \text{N}}}{{50\ \text{m}{{\text{m}}^{\text{2}}}}}[/latex]

Therefore, when we measure the elasticity of materials, we do not simply consider the force or load applied. We always consider the force or load per unit area.

We call the force or load per unit area the stress. We represent stress using the Greek letter sigma ([latex]\scriptsize \sigma[/latex]). Stress has the units [latex]\scriptsize \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex].

Take note!

Stress is force per cross-sectional unit area

[latex]\scriptsize \sigma =\displaystyle \frac{{\text{Force}}}{{\text{Cross-sectional area}}}=\displaystyle \frac{F}{A}[/latex]

Units are [latex]\scriptsize \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex]

Strain

Now let’s consider what happened when we strung five elastic bands together end-to-end to create a single band that was the same thickness as the original but five times longer.

When we string five elastic bands together to form a single longer elastic band, we see that the same load results in a change in length of this longer elastic band that is five times greater than the change in length of the original elastic band.

If a certain load stretches an elastic band with a length of [latex]\scriptsize 10\ \text{cm}[/latex] by [latex]\scriptsize 1\ \text{cm}[/latex] then this same load will stretch an identical elastic band five times longer (i.e. with a length of [latex]\scriptsize 50\ \text{cm}[/latex]) by [latex]\scriptsize 5\times 1\ \text{cm}=5\ \text{cm}[/latex]. Even though the longer elastic band is stretched more, the change in length per unit of original length is the same.

[latex]\scriptsize \displaystyle \frac{{1\ \text{cm}}}{{10\ \text{cm}}}=\displaystyle \frac{{5\ \text{cm}}}{{50\ \text{cm}}}[/latex]

Therefore, when we measure the elasticity of materials, we do not simply consider change in length. We always consider the change in length per unit of original length.

We call the change in length per unit of original length the strain. We represent strain using the Greek letter epsilon ([latex]\scriptsize \epsilon[/latex]). Because strain is [latex]\scriptsize \displaystyle \frac{{\Delta L}}{L}[/latex] it is dimensionless.

Take note!

Strain is the change in length per unit of original length
[latex]\scriptsize \epsilon =\displaystyle \frac{{\Delta L}}{L}[/latex]
[latex]\scriptsize \epsilon[/latex] is dimensionless

We sometimes represent strain as a percentage. If the strain caused by a given stress is [latex]\scriptsize 5\%[/latex], this means that if the material is ordinarily [latex]\scriptsize 1\ \text{m}[/latex] long and it is being stretched, its new length under load will be [latex]\scriptsize 1.05\ \text{m}[/latex].

Hooke’s law and the modulus of elasticity

In the section above, we defined what we mean by stress and strain. We used elastic bands to think about these concepts. It stands to reason that the greater the stress an elastic band experiences, the greater the strain it will exhibit.

The same is true of any material. The greater the stress placed on the material, the greater the strain it will exhibit.

Therefore, we can say that stress is proportional to strain. We can express this in three ways.

Stress is proportional to strain
or
[latex]\scriptsize \sigma \propto \epsilon[/latex]
or
[latex]\scriptsize \displaystyle \frac{F}{A}\propto \displaystyle \frac{{\Delta L}}{L}[/latex]

We call this relationship Hooke’s law.

But remember that if we apply a force to a material that exceeds that material’s elastic limit, the material will become permanently deformed. Therefore, Hooke’s law only applies within the material’s elastic limit.

Different materials will have different elastic limits because different materials exhibit different degrees of elasticity.

It is also true that under the same stress, different materials will deform by different amounts. They will exhibit different amounts of strain. Therefore, we can create an equation based on Hooke’s law for every kind of material as follows:

[latex]\scriptsize \sigma =k\times \epsilon \text{ or }\displaystyle \frac{F}{A}=k\times \displaystyle \frac{{\Delta L}}{L}[/latex] where [latex]\scriptsize k[/latex] is some constant value specific to the material.

The specific value of [latex]\scriptsize k[/latex] for a material tells us how much strain it will experience for a given stress. Because strain is dimensionless, the units of the constant, [latex]\scriptsize k[/latex], are [latex]\scriptsize \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex].

Let’s investigate this constant in more detail in the following activity.

Activity 1.2: Explore Hooke’s law

Time required: 15 minutes

What you need:

• a piece of paper
• a pen or pencil
• a calculator

What to do:

Imagine we have a steel wire and a piece of string. Both are [latex]\scriptsize 1\ \text{m}[/latex] long and have a cross-sectional area of [latex]\scriptsize 1\ \text{m}{{\text{m}}^{2}}[/latex]. A [latex]\scriptsize 2\ \text{kg}[/latex] mass is suspended at the end of each. The steel wire stretches by [latex]\scriptsize 0.098\ \text{mm}[/latex] and the string stretches by [latex]\scriptsize 2.48\ \text{mm}[/latex]. Assume that [latex]\scriptsize g=9.8~\text{m.s}^{-2}[/latex].

1. Calculate the stress each material is under. Remember that [latex]\scriptsize \sigma =\displaystyle \frac{F}{A}[/latex].
2. Calculate the strain each material exhibits. Remember that [latex]\scriptsize \epsilon =\displaystyle \frac{{\Delta L}}{L}[/latex].
3. Hooke’s law states that stress is proportional to strain. Find the constant, [latex]\scriptsize {{k}_{{steel}}}[/latex], needed to make the equation [latex]\scriptsize \sigma =k\times \epsilon[/latex] true for the steel wire.
4. Find the constant, [latex]\scriptsize {{k}_{{string}}}[/latex], needed to make the equation [latex]\scriptsize \sigma =k\times \epsilon[/latex] true for the string.

What did you find?

1. Each material is under the same stress. Before we can calculate the stress, we need to calculate the force the [latex]\scriptsize 2\ \text{kg}[/latex] mass is applying to the material, and we need to calculate the area in [latex]\scriptsize {{\text{m}}^{2}}[/latex].
   .
   [latex]\scriptsize F=m\times g=2~\text{kg}\times 9.8~\text{m.s}^{-2}=19.6~\text{N}[/latex]
   [latex]\scriptsize A=1\ \text{m}{{\text{m}}^{\text{2}}}=\displaystyle \frac{1}{{1\ 000\times 1\ 000}}=1\times {{10}^{{-6}}}\ {{\text{m}}^{\text{2}}}[/latex]
   [latex]\scriptsize \sigma =\displaystyle \frac{F}{A}=\displaystyle \frac{{19.6\ N}}{{1\times {{{10}}^{{-6}}}\ {{m}^{2}}}}=19.6\times {{10}^{6}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex]
2. [latex]\scriptsize \epsilon =\displaystyle \frac{{\Delta L}}{L}[/latex]
   .
   [latex]\scriptsize \begin{align*}\Delta {{L}_{{steel}}} & =0.098\ \text{mm}=0.000098\ \text{m}\\\therefore {{\epsilon }_{{steel}}} & =\displaystyle \frac{{\Delta {{L}_{{steel}}}}}{{{{L}_{{steel}}}}}=\displaystyle \frac{{0.000098\ \text{m}}}{{1\ \text{m}}}=9.8\times {{10}^{{-5}}}\end{align*}[/latex]
   .
   [latex]\scriptsize \begin{align*}\Delta {{L}_{{string}}} & =2.48\ \text{mm}=0.00248\ \text{m}\\\therefore {{\epsilon }_{{string}}} & =\displaystyle \frac{{\Delta {{L}_{{string}}}}}{{{{L}_{{string}}}}}=\displaystyle \frac{{0.00248\ \text{m}}}{{1\ \text{m}}}=2.48\times {{10}^{{-3}}}\end{align*}[/latex]
3. [latex]\scriptsize {{k}_{{steel}}}[/latex]:
   [latex]\scriptsize \begin{align*}\sigma &=k\times \epsilon \\\therefore k&=\displaystyle \frac{\sigma }{\epsilon }=\displaystyle \frac{{19.6\times {{{10}}^{6}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}}}{{9.8\times {{{10}}^{{-5}}}}}=2\times {{10}^{{11}}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\end{align*}[/latex]
4. [latex]\scriptsize {{k}_{{string}}}[/latex]:
   [latex]\scriptsize \begin{align*}\sigma &=k\times \epsilon \\\therefore k&=\displaystyle \frac{\sigma }{\epsilon }=\displaystyle \frac{{19.6\times {{{10}}^{6}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}}}{{2.48\times {{{10}}^{{-3}}}}}=7.90\times {{10}^{9}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\end{align*}[/latex]

In activity 1.2, both materials were put under the same stress, but they exhibited different amounts of strain. The amount of strain was determined by the value of [latex]\scriptsize k[/latex] in the equation [latex]\scriptsize \sigma =k\times \epsilon[/latex].

We calculated that the value of [latex]\scriptsize {{k}_{{steel}}}[/latex] was much higher (about [latex]\scriptsize 100\times[/latex]) than the value of [latex]\scriptsize {{k}_{{string}}}[/latex]. This means that steel is more elastic than string. Under the same stress, steel will exhibit less strain than string (it will deform less and quickly revert to its original shape when the stress is removed).

We call the value of [latex]\scriptsize k[/latex], the elastic modulus or the modulus of elasticity and give it the symbol [latex]\scriptsize {\mathrm E}[/latex] (uppercase Epsilon). However, many texts will simply use the letter uppercase [latex]\scriptsize E[/latex].

[latex]\scriptsize E[/latex] can be calculated for any material by placing the material under a known stress and measuring the resulting strain.

[latex]\scriptsize \begin{align*}\sigma & =E\times \epsilon \\\therefore \displaystyle \frac{F}{A} & =E\times \displaystyle \frac{{\Delta L}}{L}\\\therefore E & =\displaystyle \frac{{\displaystyle \frac{F}{A}}}{{\displaystyle \frac{{\Delta L}}{L}}}=\displaystyle \frac{F}{A}\times \displaystyle \frac{L}{{\Delta L}}\\\therefore E & =\displaystyle \frac{{F\cdot L}}{{A\cdot \Delta L}}\end{align*}[/latex]

Example 1.1

Calculate the modulus of elasticity of a copper wire with a radius of [latex]\scriptsize 2\ \text{mm}[/latex] if it exhibits a strain of [latex]\scriptsize 0.45\%[/latex] when a mass of [latex]\scriptsize 700\ \text{kg}[/latex] is suspended from it. Assume that [latex]\scriptsize g=9.8~\text{m.s}^{-2}[/latex].

Solution

We know that the strain is [latex]\scriptsize 0.45\%=0.0045[/latex].

We need to find the stress produced by suspending the [latex]\scriptsize 700\ \text{kg}[/latex] mass. First, let’s calculate the cross-sectional area of the copper wire. We can assume that the cross-sectional area is circular, and we know that the area of a circle is given by [latex]\scriptsize \text{area}=\pi {{r}^{2}}[/latex].

[latex]\scriptsize \text{area}=\pi {{r}^{2}}=\pi \times {{(2\ \text{mm})}^{2}}=12.57\ \text{m}{{\text{m}}^{\text{2}}}=12.57\times {{10}^{{-6}}}\ {{\text{m}}^{\text{2}}}[/latex]

[latex]\scriptsize \sigma=\displaystyle \frac{F}{A}=\displaystyle \frac{m\times g}{A}=\displaystyle \frac{700~\text{kg}\times 9.8~\text{m.s}^{-2}}{12.57\times 10^{-6}~\text{m}^{2}}=5.46\times 10^{8}~\text{N.m}^{-2}[/latex]

Now we can calculate the modulus of elasticity of the copper wire.
[latex]\scriptsize \begin{align*}\sigma & =E\times \epsilon \\\therefore E & =\displaystyle \frac{\sigma }{\epsilon }=\displaystyle \frac{{5.46\times {{{10}}^{8}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}}}{{0.0045}}=121.28\times {{10}^{9}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\end{align*}[/latex]

Exercise 1.1

The modulus of elasticity of a steel rod of diameter [latex]\scriptsize 10\ \text{cm}[/latex] is [latex]\scriptsize 190\times {{10}^{9}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex].

1. What will the strain on the rod be if it experiences a stress of [latex]\scriptsize 13\ 500\ \text{N}\text{.}{{\text{m}}^{{-2}}}[/latex]?
2. If a strain of [latex]\scriptsize 0.002\%[/latex] is permitted, what maximum mass can it support? Assume that [latex]\scriptsize g=9.8~\text{m.s}^{-2}[/latex].
3. Another steel rod of a different quality of steel of the same diameter experiences a strain of [latex]\scriptsize 0.025\%[/latex] when placed under the same load as in 2. Is the rod more or less elastic than the original?

The full solutions can be found at the end of the unit.

Types of stress and strain

So far in this unit, we have only considered what happens when a material, such as an elastic band, is stretched. When a material is pulled, we say it is under tensile stress and exhibits tensile strain. An example is the tensile stress and tensile strain of the chain of a tyre swing (see figure 10).

But we know that objects can also be pushed. Think of a column holding up part of a roof. In this case, the column is under compressive stress and exhibits compressive strain (see figure 11).

Instead of the material being pulled and getting longer, it gets pushed and gets shorter. However, this does not change how we use or calculate [latex]\scriptsize \Delta L[/latex] and it does not matter if the change is because the material has been stretched or compressed. We still calculate how much the length of the material has changed (see figure 12).

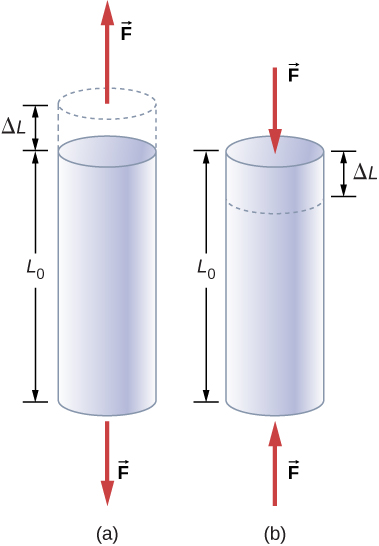
We also still use [latex]\scriptsize \sigma[/latex] to represent compressive stress and [latex]\scriptsize \epsilon[/latex] to represent compressive strain.

Did you know?

In many structures, such as bridges, the same piece of material can experience tensile and compressive stresses at the same time. This happens when a member bends and the one portion is compressed, while the other portion is stretched (see figure 13).

In both tensile and compressive stress, the force is applied at right angles or normally to the cross-sectional area. However, this does not need to be the case. There is a third important kind of stress and strain. Think what happens when you push or pull an object from the side. In this case, the force is being applied parallel to (rather than at right angles to) the cross-sectional area (see figure 14). This produces shear stress and results in shear strain.

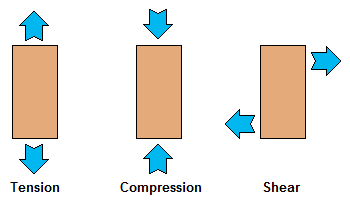
Because shear stress and strain are fundamentally different from tensile and compressive stress and strain, we use different symbols. Shear stress is represented as [latex]\scriptsize \tau[/latex] (Greek letter tau) and shear strain is represented as [latex]\scriptsize \gamma[/latex] (Greek letter gamma).

The way shear strain is measured is slightly different to tensile and compressive strain. Because the deformation is not in the same direction as the length of the object, we tend to use [latex]\scriptsize \Delta x[/latex] to indicate the amount the object has been deformed. [latex]\scriptsize \Delta x[/latex] is the amount by which the object moves from its rest position when no shear stress is applied (see figure 15). However, we still use the same basic measure of strain as [latex]\scriptsize \gamma =\displaystyle \frac{{\Delta x}}{L}[/latex].

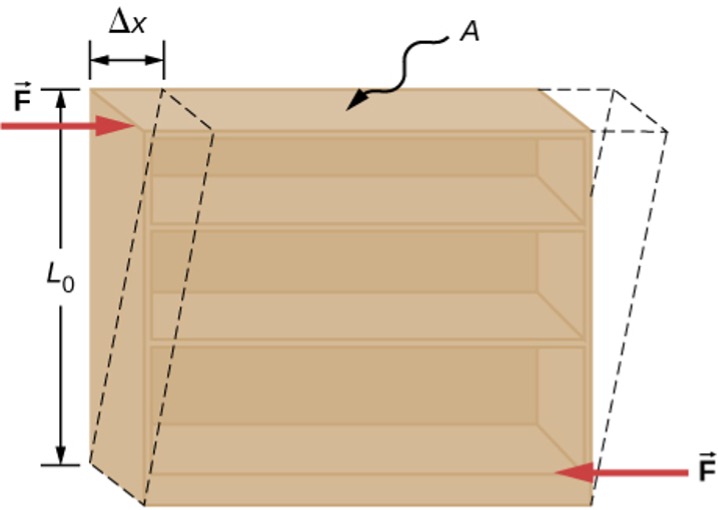
The basics of Hooke’s law still apply in that shear stress is proportional to shear strain (within the elastic limits of the material). However, we no longer refer to the modulus of elasticity as the constant. Instead, we refer to the modulus or shear or the shear modulus and use the letter [latex]\scriptsize G[/latex].

[latex]\scriptsize \begin{align*}\tau & =G\times \gamma \text{ or }\displaystyle \frac{F}{A}=G\times \displaystyle \frac{{\Delta x}}{L}\\\therefore G & =\displaystyle \frac{\tau }{\gamma }=\displaystyle \frac{{F\cdot L}}{{A\cdot \Delta x}}\end{align*}[/latex]

Exercise 1.2

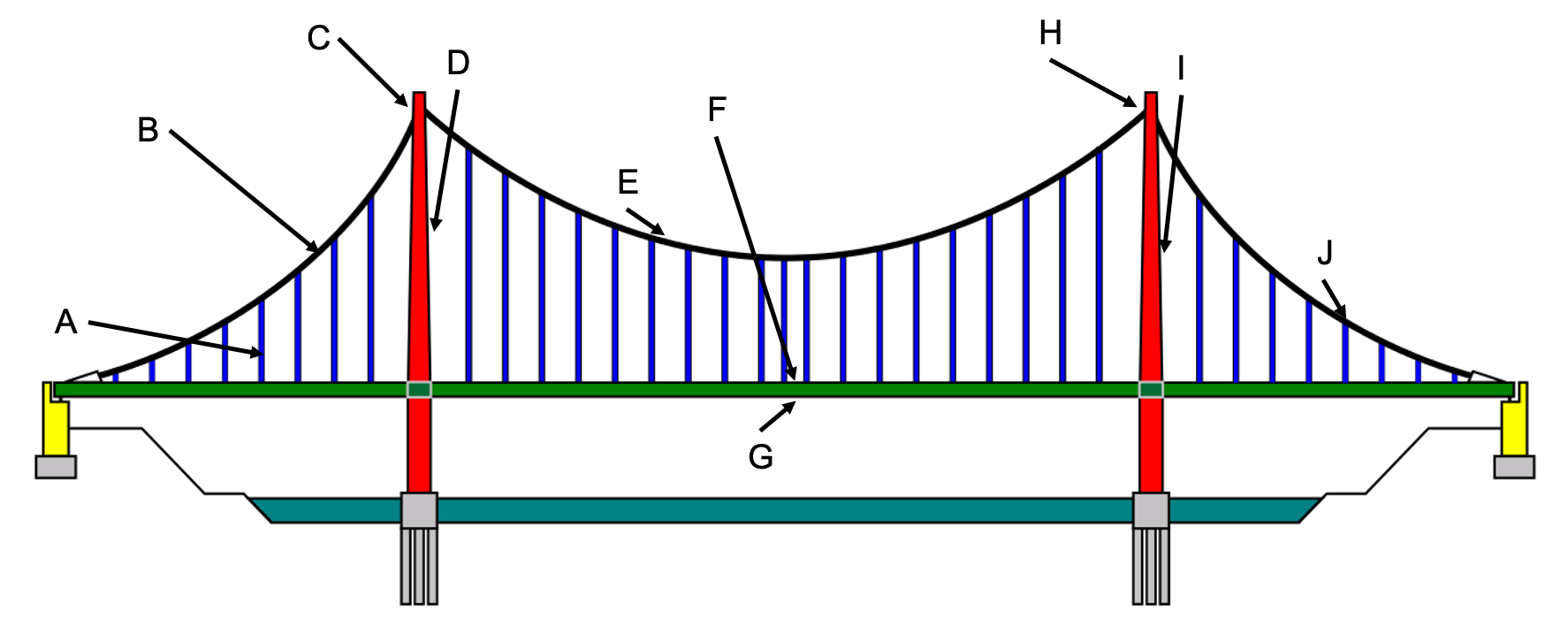
Have a look at figure 16 of a suspension bridge. Identify whether each labelled part of the bridge is under tensile stress, compressive stress or, shear stress.

The full solutions can be found at the end of the unit.

When things bend and break

So far in this unit we have looked at how materials behave when the forces applied are within their elastic limits. But we know from real life that things break or deform when the forces applied to them exceed their elastic limits. Just as different materials have different elastic limits and exhibit different amounts of elasticity, when those limits are reached or exceeded, different materials behave in different ways.

To understand this, lets follow how a material such as steel behaves as it is placed under greater and greater stress. This is called a stress test. We plot stress on the y-axis and strain on the x-axis (see figure 17).

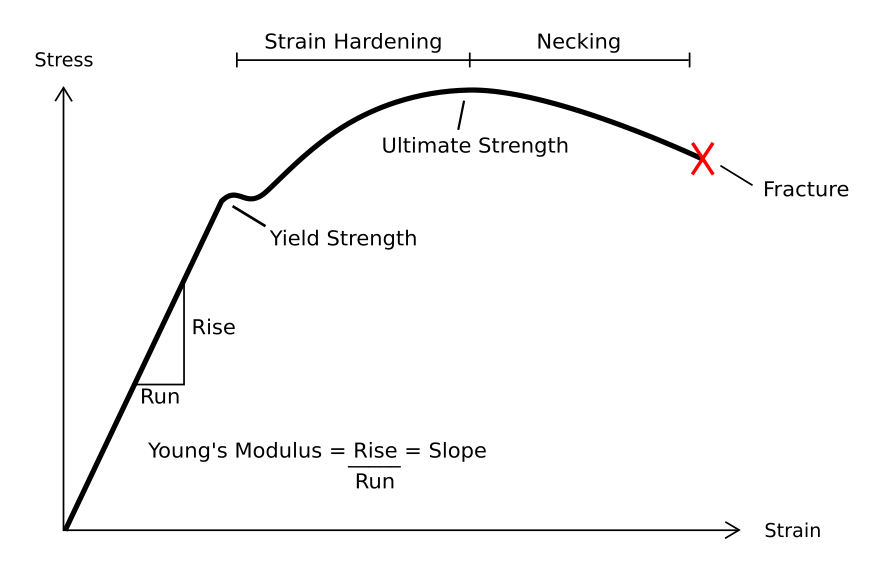
As we start to increase the stress on the rod, we increase the strain. This is Hooke’s law. Because stress is proportional to strain, we get a straight line. The gradient of this line is the modulus of elasticity (also called Young’s modulus) of the material. So far, so good. We have not reached the material’s elastic limit, so if we remove the stress, the material will assume its original shape. Any deformation in the material is reversible and so this is elastic deformation.

But if we continue to increase the stress, we will eventually reach the material’s elastic limit or yield point. After the yield point, any further deformation is permanent. This is plastic deformation. In the case of a steel rod, the material deforms but does not yet break.

If we continue to increase the stress, the material will reach its ultimate strength point. This is the most stress it can handle. After this point, less stress starts to be needed to continue to strain the material. In the case of a steel rod, you will see it start to ‘neck’. This is the term used when the diameter of the rod gets smaller (see figure 18).

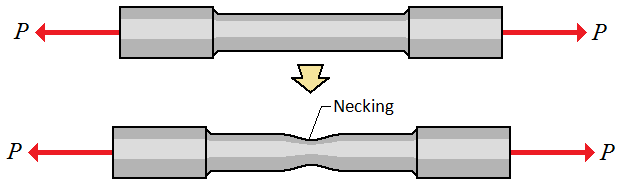
http://www.engineeringarchives.com/les_mom_necking.html – Fair use

Necking continues until the rod breaks or fractures.

Materials that have a very large plastic deformation region (i.e. will keep permanently deforming long before fracturing) are said to be ductile. Copper is a highly ductile material and this is one reason it can easily be made into long thin wires. Materials with a very small plastic deformation region (i.e. they fracture very soon after the yield limit is reached) are said to be brittle. Glass is a very brittle material. It fractures almost immediately when its yield strength is reached.

Figure 19 shows a comparison of the stress test curves of a brittle and ductile material.

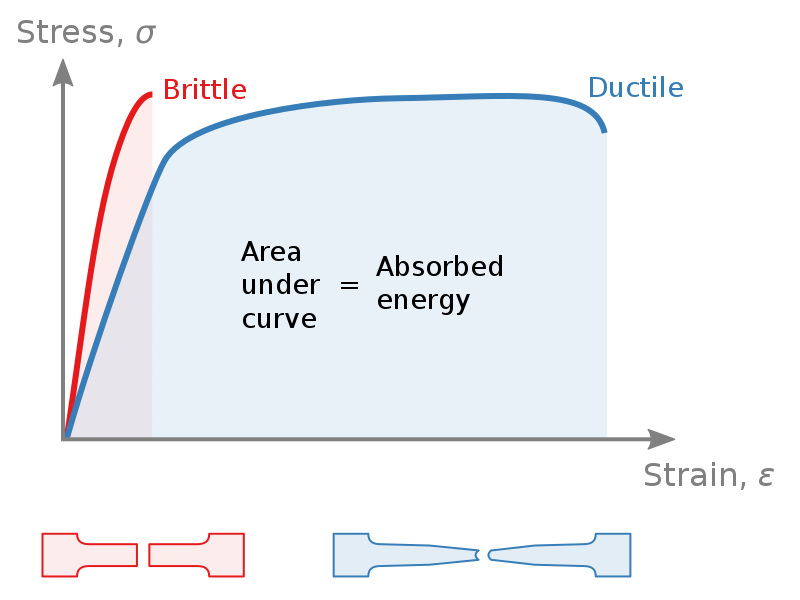
Figure 19 also illustrates that the area under each stress test curve is equivalent to the amount of energy the material can absorb. Toughness is a measure of the amount of energy a material can absorb. Tough materials can absorb a great amount of energy.

The shape of the fracture that occurs in a brittle vs ductile material is also shown in figure 19. When a brittle material fractures, there is little plastic deformation before the fracture, so the surface of the fracture tends to be granular and flat.

When a ductile material fractures, there is greater plastic deformation prior to the fracture which results in a cup and cone fracture surface.

While a steel rod in a stress test may regain its original shape after a stress is momentarily applied and then removed, that same steel rod under the same stress may permanently deform if it is placed under the stress for a long period of time. We call this creep and it is the tendency of a solid material to move slowly or deform permanently under the influence of persistent mechanical stresses.

A final important property of materials is hardness. Hardness is a measure of how resistant a solid material is to deformation when it is subjected to a compressive force.

Summary

In this unit you have learnt the following:

• Tensile stress occurs when a material is placed under a pulling deforming force normal to its cross-sectional area. The material exhibits tensile strain.
• Compressive stress occurs when a material is placed under a pushing deforming force normal to its cross-sectional area. The material exhibits compressive strain.
• Shear stress occurs when a material is placed under a sideways deforming force parallel to its cross-sectional area. The material exhibits shear strain.
• Stress is measured as the deforming force per unit area.
• Strain is measured as the change in length per unit length.
• Hooke’s law states that, within a material’s elastic limit, stress is proportional to strain.
• Young’s modulus states that the elastic modulus, or the modulus of elasticity, is the constant value for a material that relates the tensile or compressive strain it experiences for a given tensile or compressive stress.
• The shear modulus is the constant value for a material that relates the shear strain it experiences for a given shear stress.
• Elasticity is that property of a material that causes it to regain its original shape after the removal of the deforming force.
• Elastic limit is the upper limit of a deforming force up to which, if the deforming force is removed, the body regains its original form completely. Beyond this limit, the body loses its property of elasticity and becomes permanently deformed.
• Elastic deformation is non-permanent deformation of a material under stress.
• Plastic deformation is the permanent deformation of a material under stress.
• Fracture is the separation of an object or material into two or more pieces under the action of stress.
• Ductile materials have a large range of stress under which they will undergo plastic deformation.
• Brittle materials have a small range of stress under which they will undergo plastic deformation.
• Toughness is a measure of the amount of energy a material can absorb. Tough materials can absorb a great amount of energy.
• Creep is the tendency of a solid material to move slowly or deform permanently under the influence of persistent mechanical stresses.
• Hardness is a measure of how resistant a solid material is to deformation when it is subjected to a compressive force.

Unit 1: Assessment

Suggested time to complete: 15 minutes

Questions 1, 2 and 3 are adapted from NC(V) Physical Science Level 3 November 2019 question 5

1. What is the difference between an elastic material and a plastic material?
2. A spanner that was used to tighten bolts suddenly breaks off while in use.
   1. Is this because the spanner is too brittle or too ductile?
   2. What type of fracture would you expect to find at the point where the spanner broke?
3. Complete the following sentences by filling in the missing word or words.
   1. __________ stress is experienced when a metal is pushed by perpendicular forces.
   2. __________ stress is experienced when a metal is pulled by perpendicular forces.

Question 4 is adapted from NC(V) Physical Science Level 3 February 2019 question 5

4. A learner performed an experiment to investigate the relationship between the elongation (length of extension) of a spring and the force producing the elongation (length of extension). The following results were tabulated:
   

   Force in N	Elongation in cm
   [latex]\scriptsize 1.5[/latex]	[latex]\scriptsize 3.6[/latex]
   [latex]\scriptsize 3.0[/latex]	X
   [latex]\scriptsize 4.5[/latex]	[latex]\scriptsize 10.8[/latex]
   [latex]\scriptsize 6[/latex]	[latex]\scriptsize 14.4[/latex]

   1. Write an investigative question for this experiment.
   2. What is the independent variable in this investigation?
   3. Determine the value of X in the table.
   4. Name the law that was investigated.
5. Concrete has a compressive strength of [latex]\scriptsize 15\times {{10}^{6}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex]. What diameter does a circular concrete pillar need to have to be able to support a load of [latex]\scriptsize 15\ 000\ \text{N}[/latex] if the maximum allowed strain is [latex]\scriptsize 0.025\%[/latex]?

The full solutions can be found at the end of the unit.

Unit 1: Solutions

Exercise 1.1

1. .
   [latex]\scriptsize \displaystyle \begin{align*}\sigma & =E\times \epsilon \\\therefore \epsilon & =\displaystyle \frac{\sigma }{E}=\displaystyle \frac{{13\ 500\ \text{N}\text{.}{{\text{m}}^{{-2}}}}}{{190\times {{{10}}^{9}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}}}=7.1\times {{10}^{{-8}}}\end{align*}[/latex]
2. Diameter of the rod: [latex]\scriptsize 10\ \text{cm}[/latex]. Therefore, radius: [latex]\scriptsize 5\ \text{cm}=0.05\ \text{m}[/latex]
   Cross-sectional area of the rod: [latex]\scriptsize A=\pi {{r}^{2}}=\pi \times 25\ \text{c}{{\text{m}}^{\text{2}}}=7.85\times {{10}^{{-3}}}\ {{\text{m}}^{\text{2}}}[/latex]
   [latex]\scriptsize \displaystyle \sigma =E\times \epsilon =190\times {{10}^{9}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\times 0.00002=3\ 800\ 000\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex]
   .
   [latex]\scriptsize \begin{align*}\sigma &=\displaystyle \frac{F}{A}\\\therefore F&=\sigma \times A=380\ 000\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\times 7.85\times {{10}^{{-3}}}\ {{\text{m}}^{\text{2}}}=29\ 830\ \text{N}\end{align*}[/latex]
   .
   [latex]\scriptsize \begin{align*}F&=m\times g\\ \therefore m&=\displaystyle \frac{F}{a}=\displaystyle \frac{29~830~\text{N}}{9.8~\text{m.s}^{-2}}=3~043.88~\text{kg} \end{align*}[/latex]
3. For the same stress, the strain the rod experiences is greater. Therefore, the modulus of elasticity for the rod is less. Therefore, the rod is less elastic.

Back to Exercise 1.1

Exercise 1.2

Back to Exercise 1.2

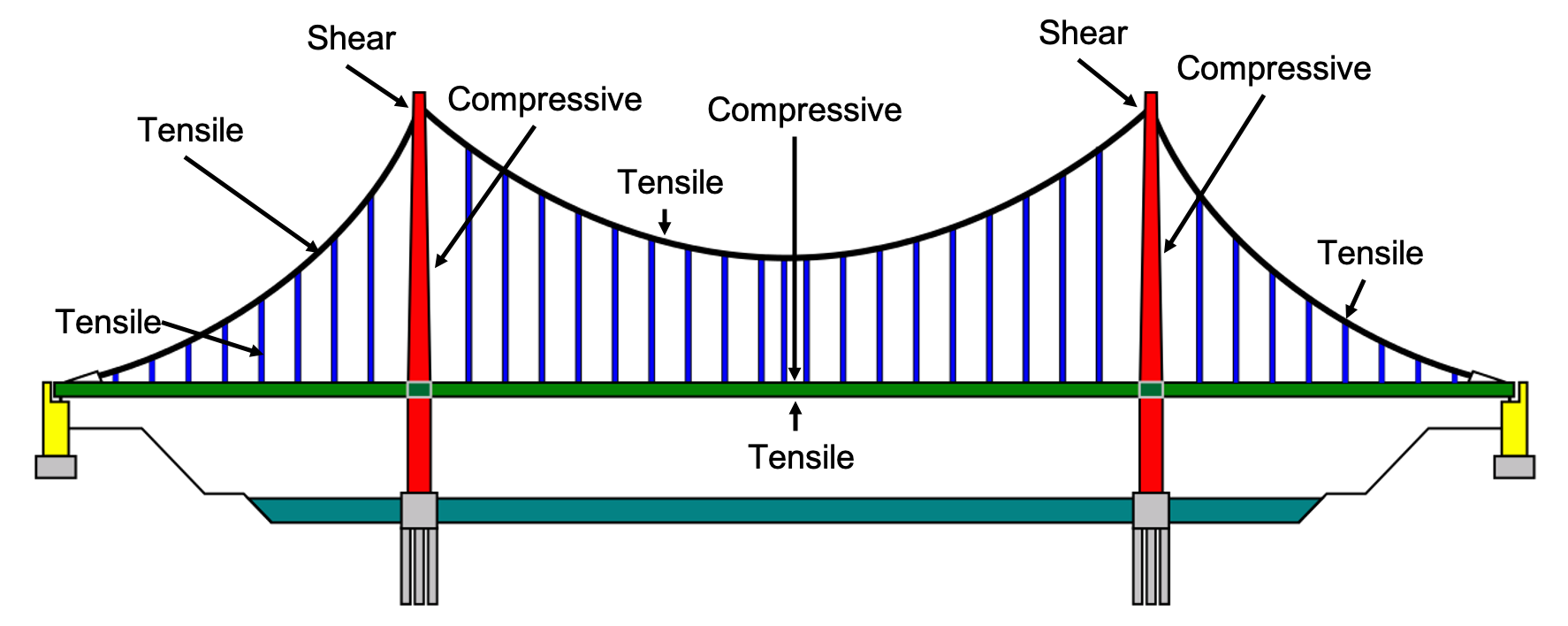
Unit 1: Assessment

1. Elastic materials regain their original shape once a deforming force (a stress) is removed. For a given stress, an elastic material will exhibit a smaller strain than a plastic material. An elastic material requires a far greater stress to permanently deform it.
2. .
   1. If a spanner suddenly breaks it is because it is too brittle. A ductile material would bend before breaking. In other words, a ductile material would have a greater range of stress under which it would undergo permanent deformation prior to fracturing (or breaking).
   2. As it is a brittle material the fracture surface would be granular and smooth.
3. .
   1. Compressive
   2. Tensile
4. .
   1. How does the amount of force (tensile stress) affect the elongation (tensile strain) of a spring?
   2. The independent variable is the amount of force with which the spring is stretched.
   3. [latex]\scriptsize 7.2\ \text{cm}[/latex]
   4. Hooke’s law
5. [latex]\scriptsize \displaystyle \sigma=E\times \epsilon =15\times {{10}^{6}}\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}\times 0.025=37\ 500\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}[/latex]
   .
   [latex]\scriptsize \displaystyle \begin{align*}\sigma &=\displaystyle \frac{F}{A}\\\therefore A&=\displaystyle \frac{F}{\sigma }=\displaystyle \frac{{15\ 000\ \text{N}}}{{37\ 500\ \text{N}\text{.}{{\text{m}}^{{\text{-2}}}}}}=0.4\ {{\text{m}}^{\text{2}}}\end{align*}[/latex]
   .
   [latex]\scriptsize \begin{align*}A & =\pi {{r}^{2}}\\\therefore {{r}^{2}} & =\displaystyle \frac{A}{\pi }=\displaystyle \frac{{0.4\ {{\text{m}}^{\text{2}}}}}{\pi }=0.13\ {{\text{m}}^{\text{2}}}\\\therefore r & =0.36\ \text{m}=36\ \text{cm}\end{align*}[/latex]

Back to Unit 1: Assessment