Mechanical Properties of matter: Describe, analyse and apply properties of gases theory
Unit 2: The gas laws
Emma Harrage
Unit outcomes
By the end of this unit you will be able to:
- Describe the difference between atmospheric and gauge pressure.
- Identify and apply the relationship between volume and pressure at a constant temperature which is Boyle’s law.
- Identify and apply the relationship between volume and temperature at a constant pressure which is Charles’s law.
- Identify and apply the relationship between pressure and temperature at a constant volume which is Guy-Lussac’s law.
- Do calculations using:
- gas law equations
- the ideal gas law equation.
What you should know
Before you start this unit, make sure you can:
- Understand the difference between a real gas and an ideal gas. Refer to level 3 subject outcome 5.4 unit 1 to revise this.
Introduction
Parts of the text in this unit were sourced from Siyavula Physical Science Gr 11 Learner’s Book, Chapter 7, released under a CC-BY licence.
There are three gas laws which are used to predict and explain how a gas will behave at different volumes, temperatures, and pressures. Boyle’s law states that if the temperature remains constant, the pressure of a fixed volume of gas is inversely proportional to the pressure. Charles’s law states that the volume of a gas is directly proportional to the temperature at a constant pressure. Guy-Lussac’s law states that pressure is directly proportional to temperature at a constant volume. These laws are then combined to form the general gas equation and the ideal gas equation.
Take note!
The following SI units are necessary for this unit:
| Variable | SI units | Other units |
| Pressure (p) | Pascals (Pa) | [latex]\scriptsize \displaystyle 760~\text{ mm Hg}=1~\text{ atm}=101~\text{ }325~\text{ Pa}=101.325\text{ }~\text{kPa}[/latex] |
| Volume (V) | [latex]\scriptsize \displaystyle {{\text{m}}^{\text{3}}}[/latex] | [latex]\scriptsize \displaystyle 1~{{\text{m}}^{\text{3}}}=1~\text{ }000~000~\text{ c}{{\text{m}}^{\text{3}}}=1~000~\text{ d}{{\text{m}}^{\text{3}}}=1~000\text{ }~\text{L}[/latex] |
| Moles (n) | mol | |
| Universal gas constant (R) | [latex]\scriptsize \displaystyle \begin{align*}{\text{J}\text{.}{{\text{K}}^{{-1}}}\text{.mo}{{\text{l}}^{{-1}}}} \end{align*}[/latex] | |
| Temperature (K) | Kelvin (K) |
Pressure is measured in several different units. We can measure pressure in millimetres of mercury (mm Hg) or pascals (Pa) or atmospheres (atm). The SI unit for pressure is Pa.
Activity 2.1: Investigate the relationship between volume and pressure
Time required: 5 minutes
What you need:
- a syringe without a needle (the plunger needs to be able to form an airtight seal)

What to do:
- Pull the plunger halfway up the syringe.
- Place your thumb over the end of the syringe (where the needle normally goes) and form an airtight seal.
- Press the plunger down.
- Once you have pushed it as hard as you can, let go of the plunger. Watch what happens.
What did you find?
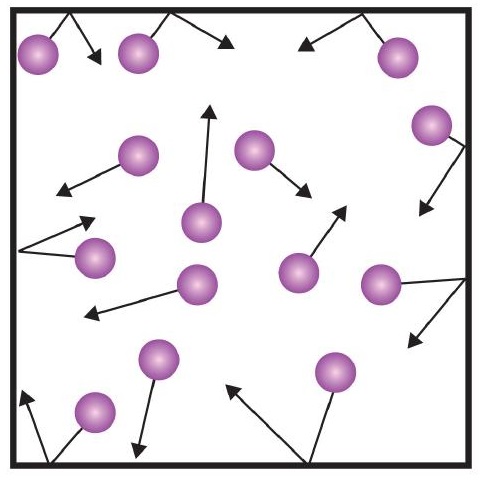
As gas particles are constantly moving, they are also constantly colliding with each other and with the walls of their container. There are forces involved as gas particles bounce off the container walls. The force generated by gas particles divided by the area of the container walls yields .
As you push it down you should notice that it becomes harder and harder to push. This is because you are forcing the gas particles into a smaller space. This increases the pressure inside the syringe because there are now more collisions between the gas particles, the sides of the syringe and the gas particles. If the volume decreases, the number of collisions increases and so the pressure will naturally increase. The opposite is true if the volume of the gas is increased. When you let go of the plunger, it would have risen – increasing the volume in the syringe. The gas particles now have a greater volume so they collide less frequently, and the pressure will decrease.
Atmospheric and gauge pressure
The air around you has weight, and it presses against everything it touches. This pressure is called , or air pressure. It is the force exerted on a surface by the air above it as gravity pulls it to Earth.
Atmospheric pressure is commonly measured with a barometer. In a barometer, a column of mercury in a glass tube rises or falls as the weight of the atmosphere changes. Meteorologists describe the atmospheric pressure by how high the mercury rises.
An atmosphere (atm) is a unit of measurement equal to the average air pressure at sea level at a temperature of [latex]\scriptsize 15\text{ }^\circ \text{C}[/latex]. One atmosphere is [latex]\scriptsize \displaystyle 1013[/latex] millibars, or [latex]\scriptsize \displaystyle 760[/latex] millimetres of mercury.
Atmospheric pressure drops as altitude increases. As the pressure decreases, the amount of oxygen available to breathe also decreases. At very high altitudes, atmospheric pressure and available oxygen get so low that people can become sick and even die.
Atmospheric pressure is an indicator of weather. When a low-pressure system moves into an area, it usually leads to cloudiness, wind, and precipitation. High-pressure systems usually lead to fair, calm weather.
If you limp into a petrol station with a nearly flat tire, you will notice the tire gauge on the airline reads nearly zero when you begin to fill it. In fact, if there were a gaping hole in your tire, the gauge would read zero, even though atmospheric pressure exists in the tire. Why does the gauge read zero? There is no mystery here. Tire gauges are simply designed to read zero at atmospheric pressure and positive when pressure is greater than atmospheric.
Similarly, atmospheric pressure adds to blood pressure in every part of the circulatory system. But atmospheric pressure has no net effect on blood flow since it adds to the pressure coming out of the heart and going back into it, too. What is important is how much greater blood pressure is than atmospheric pressure. Blood pressure measurements, like tire pressures, are thus made relative to atmospheric pressure.
It is very common for pressure gauges to ignore atmospheric pressure – that is, to read zero at atmospheric pressure. We therefore define to be the pressure relative to atmospheric pressure. Gauge pressure is positive for pressures above atmospheric pressure, and negative for pressures below it.
Boyle’s law: Pressure and volume of an enclosed gas
Let’s look at an activity to explore .
Activity 2.2: Investigate the relationship between volume and pressure
Time required: 10 minutes
What you need:
- internet access
What to do:
- Go to this simulation.
- On the main page, click on the block which says Laws.
- Click on the red dot at the bottom right of the screen. This changes the particles from heavy to light.
- Lift the handle of the pump and add light particles to the container. Whilst doing this, watch the readings on the pressure gauge.
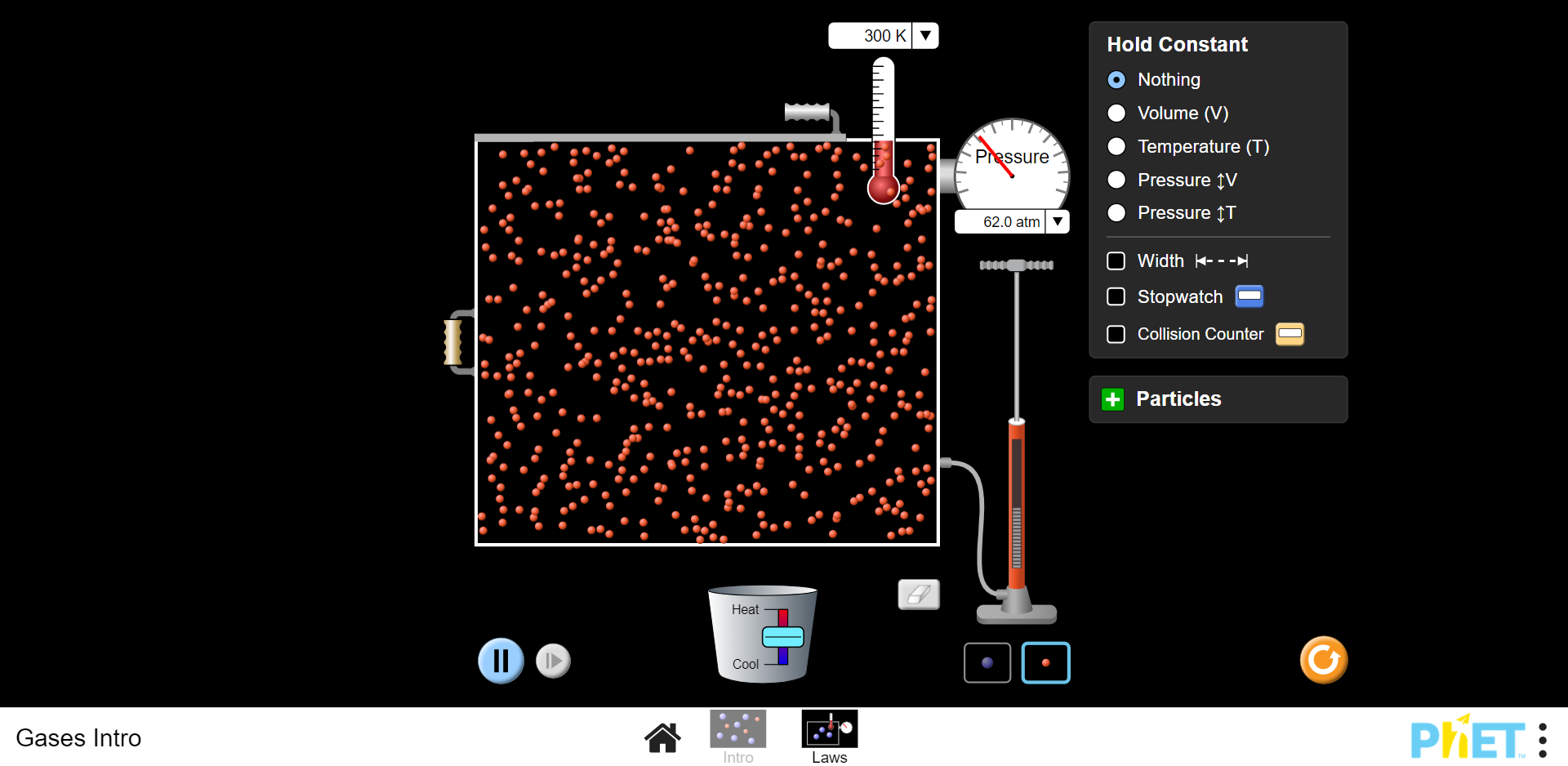
- Keep adding light particles until there are no more to add and make a note of the pressure reading.
- Change the volume of the container using the handle on the side and move it left. This will increase the volume. Make a note of the pressure reading.
- Move the handle to the right, making the container smaller whilst keeping a note of the changing pressure.
What did you find?
As particles were added, the pressure increased. This is because there were more collisions between the particles and the sides of the container.
When the size of the container increased (the volume was increased), the pressure decreased. This is because there were fewer collisions between the sides of the container and the particles.
When the volume was reduced (the container was made smaller) the pressure increased because there were more collisions between the particles and the sides of the container and the particles.
So, in conclusion, the gas molecules are moving and are a certain distance apart from one another. An increase in pressure pushes the molecules closer together, reducing the volume. If the pressure is decreased, the gases are free to move about in a larger volume. The change in volume affects the pressure.
Pressure is directly proportional to volume. As volume increases, pressure decreases and vice versa.
The pressure of a fixed quantity of gas is to the volume it occupies so long as the temperature remains constant. The relationship between pressure and volume is inversely proportional; the volume of the gas decreases when the pressure increases, and the volume increases when the pressure decreases.
Pressure is directly proportional to volume. As volume increases, pressure decreases and vice versa.
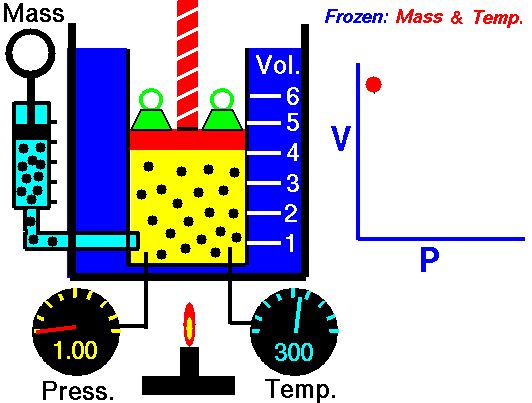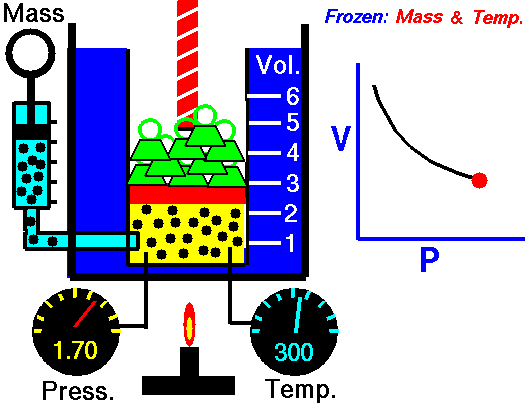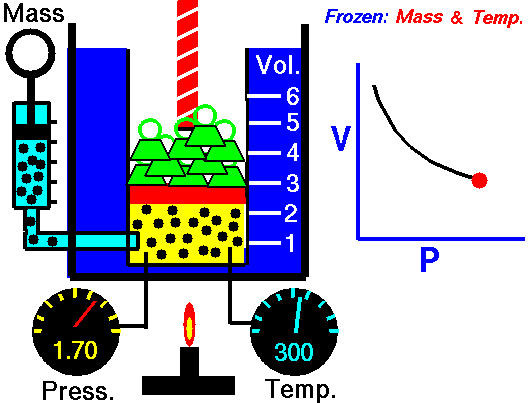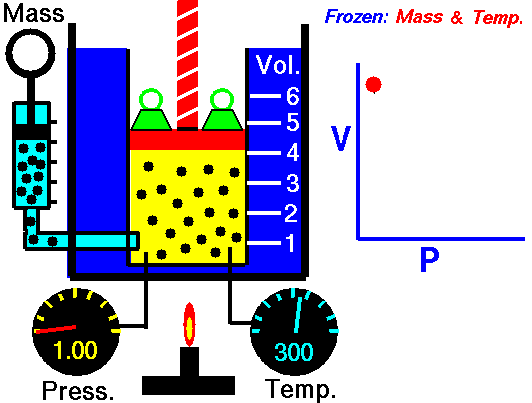
Robert Boyle (1627–1691), an English chemist, discovered that doubling the pressure of an enclosed sample of gas, while keeping its temperature constant, caused the volume of the gas to be reduced by half. Boyle’s law states that the volume of a given mass of gas is inversely proportional to the pressure when the temperature is kept constant.
We can write this relationship symbolically as: [latex]\scriptsize \displaystyle p\propto \displaystyle \frac{1}{V}[/latex]
Where [latex]\scriptsize \propto[/latex] means proportional and we write [latex]\scriptsize \displaystyle \frac{1}{V}[/latex] to show that the proportionality is inverse.
Mathematically, Boyle’s law can be expressed by the equation: [latex]\scriptsize \displaystyle pV=k[/latex] = Pressure multiplied by volume equals some constant k. Where P is the pressure of the gas, V is the volume of the gas, and k is a constant for a given sample of gas and depends only on the mass of the gas and the temperature.
This equation means that, assuming the temperature and amount of gas is constant, multiplying any pressure and volume values for a fixed amount of gas will always give the same value (k). For example:
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{1}}{{V}_{1}}&=k\\{{p}_{2}}{{V}_{2}}&=k\end{align*}[/latex]
where the subscripts 1 and 2 refer to two pairs of pressure and volume readings for the same mass of any gas at the same temperature.
From this, we can then say that: [latex]\scriptsize \displaystyle {{p}_{1}}{{V}_{1}}=\text{ }{{p}_{2}}{{V}_{2}}[/latex]
When using this formula, any units for pressure and volume can be used, as long as they are the same.
Boyle’s law requires two conditions. First, the amount of gas must stay constant. If you let a little of the air escape from the container in which it is enclosed, the pressure of the gas will decrease along with the volume, and the inverse proportion relationship is no longer valid. Second, the temperature must stay constant. Cooling or heating matter generally causes it to contract or expand, or the pressure to decrease or increase. In the experiment, if we were to heat up the gas, it would expand and require a greater force to keep the plunger at a given position. Again, the proportionality would no longer be valid.
Example 2.1
A sample of helium occupies a volume of [latex]\scriptsize \displaystyle 160\text{ c}{{\text{m}}^{\text{3}}}[/latex] at [latex]\scriptsize \displaystyle 100\text{ kPa}[/latex] and . What volume will it occupy if the pressure is adjusted to [latex]\scriptsize \displaystyle 80\text{ kPa}[/latex] and the temperature remains unchanged?
Solution
Step 1: Write down all the information given about the gas
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{1}}&=100\text{ kPa}\\{{p}_{2}}&=80\text{ kPa}\\{{V}_{1}}&=160\text{ c}{{\text{m}}^{\text{3}}}\\{{V}_{2}}&=?\end{align*}[/latex]
Step 2: Use an appropriate gas law equation to calculate the unknown variable
Because the temperature of the gas stays the same, the following equation can be used: [latex]\scriptsize \displaystyle {{p}_{2}}{{V}_{2}}=\text{ }{{p}_{1}}{{V}_{1}}[/latex]
Step 3: Substitute the known values into the equation
Make sure that the units for each variable are the same. Calculate the unknown variable.
[latex]\scriptsize \displaystyle \begin{align*}\left( {80} \right){{V}_{2}}&=\left( {100} \right)\left( {160} \right)\\ & =16\text{ }000\\&=200\text{ c}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
The volume occupied by the gas at a pressure of [latex]\scriptsize \displaystyle 80\text{ kPa}[/latex] is [latex]\scriptsize 200\text{ c}{{\text{m}}^{\text{3}}}[/latex].
Check your answer: Boyle’s law states that the pressure is inversely proportional to the volume. Since the pressure decreased the volume must increase. The answer for the volume is greater than the initial volume and so our answer is reasonable.
Example 2.2
The volume of a sample of gas is increased from [latex]\scriptsize \displaystyle 2.5\text{ L}[/latex] to [latex]\scriptsize \displaystyle 2.8\text{ L}[/latex] while a constant temperature is maintained. What is the final pressure of the gas at the new volume condition, if the initial pressure is [latex]\scriptsize \displaystyle 695\text{ Pa}[/latex]?
Solution
Step 1: Write down all the information given about the gas
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{1}}&=2.5\text{ L}\\{{V}_{2}}&=2.8\text{ L}\\{{p}_{1}}&=695\text{ Pa}\\{{p}_{2}}&=?\end{align*}[/latex]
Step 2: Choose a relevant gas law equation to calculate the unknown variable
The sample of gas is at constant temperature and so we can use Boyle’s law: [latex]\scriptsize \displaystyle {{p}_{2}}{{V}_{2}}=\text{ }{{p}_{1}}{{V}_{1}}[/latex]
Step 3: Substitute the known values into the equation
Make sure that the units for each variable are the same. Calculate the unknown variable.
[latex]\scriptsize \displaystyle \begin{align*}\left( {2,8} \right){{p}_{2}}&=\left( {695} \right)\left( {2.5} \right)\\ & =1\text{ }737.5\\ & =620.54\text{ kPa}\end{align*}[/latex]
The pressure of the gas at a volume of [latex]\scriptsize \displaystyle 2.8\text{ L}[/latex] is [latex]\scriptsize \displaystyle 620.5\text{ kPa}[/latex].
Check your answer: Boyle’s law states that the pressure is inversely proportional to the volume. Since the volume increased the pressure must decrease. The answer of [latex]\scriptsize \displaystyle 620.5\text{ kPa}[/latex] is less than the initial pressure and so our answer is reasonable.
Example 2.3
A sample of oxygen gas has a volume of [latex]\scriptsize \displaystyle 425\text{ mL}[/latex] when the pressure is equal to [latex]\scriptsize \displaystyle \text{387 kPa}[/latex]. The gas is allowed to expand into a [latex]\scriptsize \displaystyle \text{1}\text{.75 L }\!\!~\!\!\text{ }[/latex] container. Calculate the new pressure of the gas.
Solution
Step 1: List the known quantities and plan the problem
[latex]\scriptsize \displaystyle \begin{align*}{p}_{1}&=387\text{ kPa}\\ {V}_{1}&=425\text{ ml}\\ {V}_{2}&=1.75\text{ L}=1750\text{ ml}\\ {p}_{2}&=?\text{ kPa} \end{align*}[/latex]
It is important that the two volumes are expressed in the same units, so V2 has been converted to mL.
Step 2: Rearrange the equation algebraically to solve for P2
[latex]\scriptsize \displaystyle {{p}_{2}}=\displaystyle \frac{{{{p}_{1}}x{{V}_{1}}}}{{{{V}_{2}}}}[/latex]
Step 3: Substitute the known quantities into the equation and solve
[latex]\scriptsize {{p}_{2}}=\displaystyle \frac{{387x425}}{{1750}}=94.0\text{ kPa}[/latex]
Check your answer: The volume has increased to slightly over [latex]\scriptsize \displaystyle 4[/latex] times its original value and so the pressure is decreased by about a quarter.
Exercise 2.1
- An unknown gas has an initial pressure of [latex]\scriptsize \displaystyle 150\text{ kPa}[/latex] and a volume of [latex]\scriptsize \displaystyle 1\text{ L}[/latex]. If the volume is increased to [latex]\scriptsize \displaystyle 1.5\text{ L}[/latex], what will the pressure be now?
- A bicycle pump contains [latex]\scriptsize \displaystyle 250\text{ c}{{\text{m}}^{\text{3}}}[/latex] of air at a pressure of [latex]\scriptsize \displaystyle 90\text{ kPa}[/latex]. If the air is compressed, the volume is reduced to [latex]\scriptsize \displaystyle 200\text{ c}{{\text{m}}^{\text{3}}}[/latex]. What is the pressure of the air inside the pump?
- The air inside a syringe occupies a volume of [latex]\scriptsize \displaystyle 10\text{ c}{{\text{m}}^{3}}[/latex] and exerts a pressure of [latex]\scriptsize \displaystyle 100\text{ kPa}[/latex]. If the end of the syringe is sealed and the plunger is pushed down, the pressure increases to [latex]\scriptsize \displaystyle 120\text{ kPa}[/latex]. What is the volume of the air in the syringe?
The full solutions can be found at the end of the unit.
Charles’s law: Volume and temperature of an enclosed gas
When the temperature of a gas increases, so does the average speed of its molecules. The molecules collide with the walls of the container more often and with greater impact. In a container that can expand, these collisions will push back the walls, so that the gas occupies a greater volume than it did at the start.
Activity 2.3: Demonstrate Charles’s Law
Time required: 15 minutes
What you need:
- an empty glass bottle
- a balloon
- a pot
- water
- a hot plate
What to do:
- Fill the pot about [latex]\scriptsize \displaystyle \frac{1}{3}[/latex] full of water and place it on the hot plate and allow the water to boil.
- Place the balloon over the neck of the bottle and stand the bottle in the pot.
- Observe what happens.
What did you find?
After a few minutes, you should see the balloon filling. As the air inside the bottle is heated, the pressure also increases. This causes the air in the bottle to increase in volume, and because the glass bottle is a fixed shape and cannot expand, the warmed gas fills the balloon.
The temperature and volume of the gas are directly proportional to each other. As one increases, so does the other.
French physicist Jacques Charles (1746–1823) studied the effect of temperature on the volume of a gas at constant pressure. states that the volume of a given mass of gas is directly proportional to the absolute temperature of the gas when pressure is kept constant. The absolute temperature is the temperature measured with the Kelvin scale. The Kelvin scale must be used because zero on the Kelvin scale corresponds to a complete stop of molecular motion.
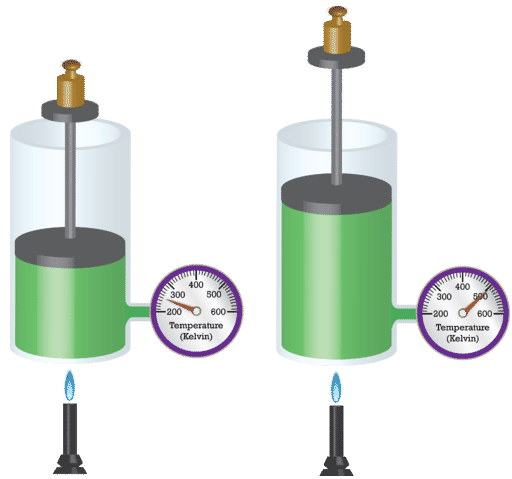
Mathematically, the direct relationship of Charles’s law can be represented by the following equation: [latex]\scriptsize \displaystyle \displaystyle \frac{V}{T}=k[/latex]
As with Boyle’s law, k is constant only for a given gas sample.
| Temperature (K) | Volume (mL) |
| [latex]\scriptsize 50[/latex] | [latex]\scriptsize 20[/latex] |
| [latex]\scriptsize \displaystyle 100[/latex] | [latex]\scriptsize 40[/latex] |
| [latex]\scriptsize \displaystyle 150[/latex] | [latex]\scriptsize 60[/latex] |
| [latex]\scriptsize 200[/latex] | [latex]\scriptsize 80[/latex] |
| [latex]\scriptsize 400[/latex] | [latex]\scriptsize 160[/latex] |
| [latex]\scriptsize 800[/latex] | [latex]\scriptsize 320[/latex] |
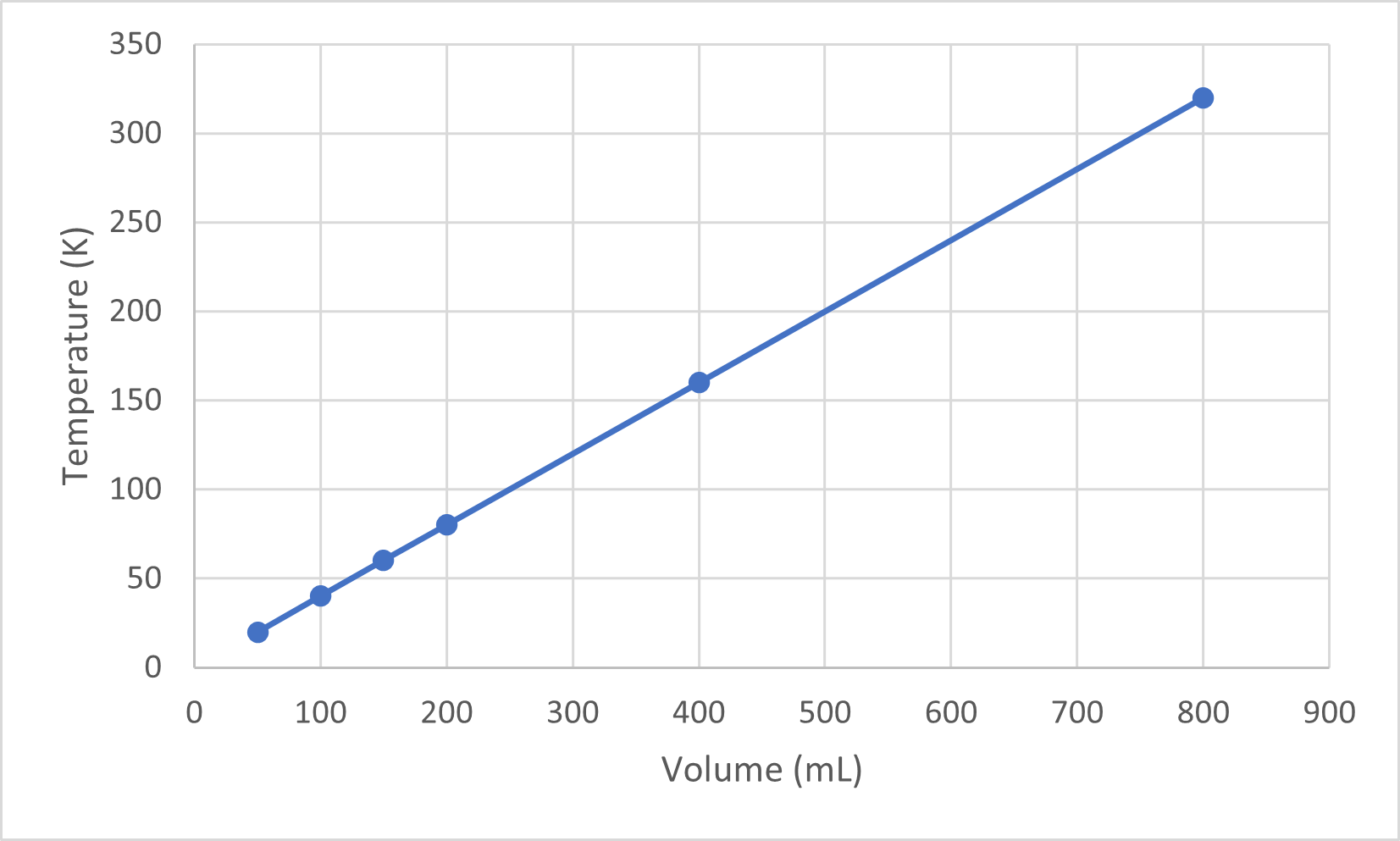
When the data from table 1 is plotted you can see it forms a straight line which confirms that temperature is directly proportional to volume.
Notice that the line goes exactly toward the origin, meaning that as the absolute temperature of the gas approaches zero, its volume approaches zero. However, when a gas is brought to extremely cold temperatures, its molecules would eventually condense into the liquid state before reaching absolute zero. The temperature at which this change into the liquid state occurs varies for different gases.
Charles’s law can be used to compare changing conditions for a gas. We use [latex]\scriptsize \displaystyle {{V}_{1}}[/latex] and [latex]\scriptsize \displaystyle {{T}_{1}}[/latex] to stand for the initial volume and temperature of a gas, while [latex]\scriptsize \displaystyle {{V}_{2}}[/latex] and [latex]\scriptsize \displaystyle {{T}_{2}}[/latex] stand for the final volume and temperature. The mathematical relationship of Charles’s law becomes: [latex]\scriptsize \displaystyle \frac{{{{V}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{V}_{2}}}}{{{{T}_{2}}}}[/latex]
When using this formula, any units can be used for volume, but the temperature must be in Kelvin.
Example 2.4
A balloon is filled to a volume of [latex]\scriptsize \displaystyle 2.20\text{ L}~[/latex] at a temperature of [latex]\scriptsize \displaystyle 22\text{ }{}^{\text{0}}\text{C}[/latex]. The balloon is then heated to a temperature of [latex]\scriptsize \displaystyle 71{{\text{ }}^{\text{0}}}\text{C}[/latex]. Find the new volume of the balloon.
Solution
Step 1: Identify the given information and what the problem is asking you to find
Do not forget that the temperatures given need to be converted to Kelvin from Celsius.
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{1}}&=2.20\text{L}\\{{T}_{1}}&=22\text{ }^\circ \text{C = 273 + 22= 295 K}\\{{T}_{2}}&=71\text{ }^\circ \text{C}=273+71=344\text{ K}\\{{V}_{2}}&=\text{ ?}\end{align*}[/latex]
Step 2: Rearrange the equation
[latex]\scriptsize {{V}_{2}}=\displaystyle \frac{{{{V}_{1}}x{{T}_{2}}}}{{{{T}_{1}}}}[/latex]
Step 3: Substitute the known quantities into the equation and solve
[latex]\scriptsize \begin{align*}{{V}_{2}}&=\displaystyle \frac{{2.20x344}}{{295}}\\{{V}_{2}}&=2.57\text{ L}\end{align*}[/latex]
Check your answer: The volume increases as the temperature increases.
Example 2.5
A sample of a gas has an initial volume of [latex]\scriptsize \displaystyle 34.8\text{ d}{{\text{m}}^{3}}[/latex] and an initial temperature of [latex]\scriptsize \displaystyle -67\text{ }\!\!^\circ\!\!\text{ C}[/latex]. What must the temperature of the gas be for its volume to be [latex]\scriptsize \displaystyle 25.0\text{ d}{{\text{m}}^{3}}[/latex]?
Solution
Step 1: Identify the given information and what the problem is asking you to find
Do not forget to convert the temperature from Celsius to Kelvin.
[latex]\scriptsize \displaystyle \begin{align*}{T}_{1}~&=\text{-}67\text{ }^\text{o}\text{C =273+ -67= 206 K}\\ {V}_{1}~&=34.8\text{ d}{\text{m}}^{3}\\ {V}_{2}~&=25.0\text{ d}{\text{m}}^{3}\\ {T}_{2}~&=?\text{ K} \end{align*}[/latex]
Step 2: Substitute the known quantities into the equation and solve
[latex]\scriptsize {{T}_{2}}=\displaystyle \frac{{25.0x206}}{{34.8}}=148\text{ K}[/latex]
Check your answer: [latex]\scriptsize 148\text{ K = -125 }^\circ \text{C}[/latex]. As volume decreases the temperature decreases.
Exercise 2.2
- If:
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{1}}&=623\text{ mL}\\{{T}_{1}}&=\text{ }255\text{ }\!\!^\circ\!\!\text{ C}\\{{V}_{2}}&=\text{ }277\text{ mL}\end{align*}[/latex]
What is T2? - A sample of nitrogen monoxide (NO) gas is at a temperature of [latex]\scriptsize 8\text{ }^\circ \text{C}[/latex] and occupies a volume of [latex]\scriptsize \displaystyle 4.4\text{ d}{{\text{m}}^{\text{3}}}[/latex]. What volume will the sample of gas have if the temperature is increased to [latex]\scriptsize 25\text{ }^\circ \text{C}[/latex]?
- A sample of oxygen gas is at a temperature of [latex]\scriptsize \displaystyle 340\text{ K}[/latex] and occupies a volume of [latex]\scriptsize \displaystyle 1.2\text{ d}{{\text{m}}^{3}}[/latex]. What temperature will the sample of gas be at if the volume is decreased to [latex]\scriptsize \displaystyle 200\text{ c}{{\text{m}}^{3}}[/latex]?
The full solutions can be found at the end of the unit.
The relationship between temperature and pressure
The pressure of a gas is directly proportional to its temperature, if the volume is kept constant. Remember that as the temperature of a gas increases, so does the kinetic energy of the particles in the gas. This causes the particles in the gas to move more rapidly and to collide with each other and with the side of the container more often. Since pressure is a measure of these collisions, the pressure of the gas increases with an increase in temperature. The pressure of the gas will decrease if its temperature decreases.
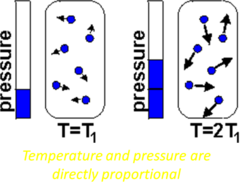
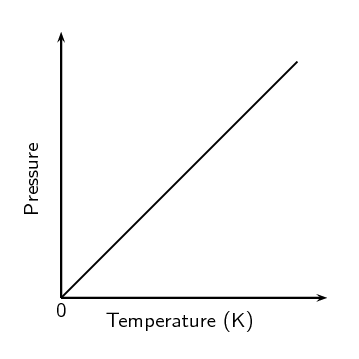
The graph in figure 8 also illustrates a direct relationship. As a gas is cooled at constant volume, its pressure continually decreases until the gas condenses to a liquid.
Mathematically this can be written as:
[latex]\scriptsize T\alpha p[/latex]
so: [latex]\scriptsize p=kT[/latex] and [latex]\scriptsize k=\displaystyle \frac{p}{T}[/latex]
and provided that the volume of gas stays the same: [latex]\scriptsize \displaystyle \frac{{{{P}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{P}_{2}}}}{{{{T}_{2}}}}[/latex]
Example 2.6
The gas in an aerosol can is under a pressure of [latex]\scriptsize \displaystyle 3.00\text{ atm}[/latex] at a temperature of [latex]\scriptsize 25\text{ }^\circ \text{C}[/latex]. It is dangerous to dispose of an aerosol can by incineration. What would the pressure in the aerosol can be at a temperature of [latex]\scriptsize 845\text{ }^\circ \text{C}[/latex]?
Solution
Step 1: State what is known, remembering to convert the temperatures from Celsius to Kelvin
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{1}}&=3.00\;\text{atm}\\{{T}_{1}}&=25\text{ }^\circ \text{C= 25+273=298 K}\\{{T}_{2}}&=845{{\text{ }}^{^\circ }}\text{C= 845+273=1118 K}\\{{p}_{2}}&=?\text{ atm}\end{align*}[/latex]
Step 2: Rearrange the equation [latex]\scriptsize \displaystyle \frac{{{{P}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{P}_{2}}}}{{{{T}_{2}}}}[/latex] to solve for [latex]\scriptsize {{p}_{2}}[/latex]
[latex]\scriptsize \begin{align*}{{p}_{2}}&=\displaystyle \frac{{{{p}_{1}}\text{x }{{T}_{2}}}}{{{{T}_{1}}}}\\{{p}_{2}}&=\displaystyle \frac{{3.00\text{ x }1118}}{{298}}\\{{p}_{2}}&=11.25\text{ atm}\end{align*}[/latex]
Check your answer: The pressure increases by a large amount because of the large increase in the temperature.
Example 2.7
At a temperature of [latex]\scriptsize \displaystyle 298\text{ K}[/latex], a certain amount of oxygen (O2) gas has a pressure of [latex]\scriptsize \displaystyle 0.4\text{ atm}[/latex]. What temperature will the gas be at if its pressure is increased to [latex]\scriptsize \displaystyle 0.7\text{ atm}[/latex]?
Solution
Step 1: Write down all the given information about the gas
[latex]\scriptsize \begin{align*}{{T}_{1}}&=298\text{ K}\\{{p}_{1}}&=0.4\text{ atm}\\{{p}_{2}}&=0.7\text{ atm}\\{{T}_{2}}&=?\text{ atm}\end{align*}[/latex]
Step 2: Choose a relevant gas law equation that will allow you to calculate the unknown variable
The volume is kept constant while the pressure and temperature are being varied. The amount of gas is also kept constant and so we can use the pressure-temperature relation:
[latex]\scriptsize \displaystyle \frac{{{{P}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{P}_{2}}}}{{{{T}_{2}}}}[/latex]
Step 3: Substitute the known values into the equation and calculate the unknown variable
[latex]\scriptsize \begin{align*}{{T}_{2}}&=\displaystyle \frac{{0.4}}{{298}}=\displaystyle \frac{{0.7}}{{{{T}_{2}}}}\\{{T}_{2}}&=\displaystyle \frac{{0.7}}{{0.0013}}\\{{T}_{2}}&=538.46\text{ K}\end{align*}[/latex]
Check your answer: The temperature has increased as the pressure increased.
Example 2.8
A fixed volume of carbon monoxide (CO) gas has a temperature of [latex]\scriptsize 32\text{ }^\circ \text{C}[/latex] and a pressure of [latex]\scriptsize \displaystyle 680\text{ Pa}[/latex]. If the temperature is decreased to [latex]\scriptsize 15\text{ }^\circ \text{C}[/latex] what will the pressure be?
Solution
Step 1: Write down the known information.
Remember to convert the temperature from Celsius to Kelvin.
[latex]\scriptsize \begin{align*}{{T}_{1}}&=32\text{ }\!\!^\circ\!\!\text{ C}=32+273=305\text{ K}\\{{T}_{2}}&=15\text{ }^\circ \text{C =15+273 =288 K}\\{{p}_{1}}&=680\text{ Pa}\\{{p}_{2}}&=?\text{ Pa}\end{align*}[/latex]
Step 2: Choose a relevant gas law equation that will allow you to calculate the unknown variable.
Substitute the known values into the equation to calculate the unknown variable.
[latex]\scriptsize \displaystyle \begin{align*}\displaystyle \frac{{{{p}_{2}}}}{{{{T}_{2}}}}&=\displaystyle \frac{{{{p}_{1}}}}{{{{T}_{1}}}}\\\displaystyle \frac{{{{p}_{2}}}}{{288}}&=\displaystyle \frac{{680}}{{305}}\\\displaystyle \frac{{{{p}_{2}}}}{{288}}&=2.229\\{{p}_{2}}&=288\text{ x }2.229\\{{p}_{2}}&=641.95\text{ Pa}\end{align*}[/latex]
Check your answer: The temperature decreases and so the pressure must decrease.
Exercise 2.3
- A cylinder that contains methane gas is kept at a temperature of [latex]\scriptsize 15\text{ }^\circ \text{C}[/latex] and exerts a pressure of [latex]\scriptsize \displaystyle 7\text{ atm}[/latex]. If the temperature of the cylinder increases to [latex]\scriptsize 25{{\text{ }}^{^\circ }}\text{C}[/latex], what pressure does the gas now exert?
- A cylinder of acetylene gas is kept at a temperature of [latex]\scriptsize \displaystyle 291\text{ K}[/latex]. The pressure in the cylinder is [latex]\scriptsize \displaystyle 5\text{ atm}[/latex]. This cylinder can withstand a pressure of [latex]\scriptsize \displaystyle 8\text{ atm}[/latex] before it explodes. What is the maximum temperature that the cylinder can safely be stored at?
The full solutions can be found at the end of the unit.
The general gas law
All the gas laws we have described so far rely on the fact that the amount of gas and one other variable (temperature, pressure, or volume) remains constant. Since this is unlikely to be the case most times, it is useful to combine the relationships into one equation. We will use Boyle’s law and the pressure-temperature relation to work out the general gas equation.
Boyle’s law: [latex]\scriptsize \displaystyle p\propto \displaystyle \frac{1}{V}[/latex] (constant T)
In other words, pressure is inversely proportional to the volume at constant temperature.
Pressure-temperature relation: [latex]\scriptsize \displaystyle p\propto T[/latex] (constant V)
In other words, pressure is also directly proportional to the temperature at constant volume.
If we now vary both the volume and the temperature, the two proportionalities will still hold, but will be equal to a different proportionality constant.
So we can combine these relationships, to get:
[latex]\scriptsize \displaystyle p\propto TV[/latex]
Note that this says that the pressure is still directly proportional to the temperature and inversely proportional to the volume.
If we introduce the proportionality constant, k, we get:
[latex]\scriptsize \displaystyle p=kTV[/latex]
or rearranging the equation:
[latex]\scriptsize \displaystyle pV=kT[/latex]
We can also rewrite this relationship as follows:
[latex]\scriptsize \displaystyle \displaystyle \frac{{pV}}{T}=k[/latex]
Provided the mass of the gas stays the same, we can also say that:
[latex]\scriptsize \displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}[/latex]
In the above equation, the subscripts [latex]\scriptsize 1[/latex] and [latex]\scriptsize 2[/latex] refer to two pressure and volume readings for the same mass of gas under different conditions. This is known as the general gas equation. Remember that the general gas equation only applies if the mass (or number of moles) of the gas is fixed. Temperature is always in Kelvin and the units used for pressure and volume must be the same on both sides of the equation.
Example 2.9
At the beginning of a journey, a truck tyre has a volume of [latex]\scriptsize \displaystyle 30\text{ d}{{\text{m}}^{\text{3}}}[/latex] and an internal pressure of [latex]\scriptsize \displaystyle 170\text{ }kPa[/latex]. The temperature of the tyre is [latex]\scriptsize 16\text{ }^\circ \text{C}[/latex]. By the end of the trip, the volume of the tyre has increased to [latex]\scriptsize \displaystyle 32\text{ d}{{\text{m}}^{\text{3}}}[/latex] and the temperature of the air inside the tyre is [latex]\scriptsize 40\text{ }^\circ \text{C}[/latex]. What is the tyre pressure at the end of the journey?
Solution
Step 1: Write down all the given information about the gas
Remember to convert the temperatures from Celsius to Kelvin.
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=16\text{ }^\circ \text{C}=273+16=289\text{ K}\\{{T}_{2}}&=40\text{ }^\circ \text{C= }273+40=313\text{ K}\\{{V}_{1}}&=30\text{ d}{{\text{m}}^{\text{3}}}\\{{V}_{2}}&=32\text{ d}{{\text{m}}^{\text{3}}}\text{ }\\{{p}_{1}}&=170\text{ kPa}\\{{p}_{2}}&=?\text{ kPa}\end{align*}[/latex]
Step 2: Choose a relevant gas law equation that will allow you to calculate the unknown variable
Temperature, pressure, and volume are all varying so we must use the general gas equation:
[latex]\scriptsize \displaystyle \displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}=\displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}[/latex]
Step 3: Substitute the known values into the equation and calculate the unknown variable
[latex]\scriptsize \begin{align*}\displaystyle \frac{{(32){{p}_{2}}}}{{313}}&=\displaystyle \frac{{(170)(30)}}{{289}}\\\displaystyle \frac{{(32){{p}_{2}}}}{{313}}&=17.647\\(32){{p}_{2}}&=5523.529\\{{p}_{2}}&=172.61\text{ kPa}\end{align*}[/latex]
Check your answer: The volume and temperature increased so the pressure will also increase.
Example 2.10
A cylinder of propane gas is kept at a temperature of [latex]\scriptsize \displaystyle 298\text{ K}[/latex]. The gas exerts a pressure of [latex]\scriptsize \displaystyle 5\text{ atm}[/latex] and the cylinder holds [latex]\scriptsize \displaystyle 4\text{ d}{{\text{m}}^{\text{3}}}[/latex] of gas. If the pressure of the cylinder increases to [latex]\scriptsize \displaystyle 5.2\text{ atm}[/latex] and [latex]\scriptsize \displaystyle 0.3\text{ d}{{\text{m}}^{\text{3}}}[/latex] of gas leaks out, what temperature is the gas now at?
Solution
Step 1: Write down all the given information about the gas
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=298~\text{K}\\{{T}_{2}}&=?\\{{V}_{1}}&=4~\text{d}{{\text{m}}^{\text{3}}}\\{{V}_{2}}&=4-0,3=3.7~\text{d}{{\text{m}}^{\text{3}}}\\{{p}_{1}}&=5~\text{atm}\\{{p}_{2}}&=5.2~\text{atm}\end{align*}[/latex]
Step 2: Choose a relevant gas law equation that will allow you to calculate the unknown variable
Since volume, pressure, and temperature are varying, we must use the general gas equation:
[latex]\scriptsize \displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}[/latex]
Step 3: Substitute the known values into the equation and calculate the unknown variable
[latex]\scriptsize \begin{align*}\displaystyle \frac{{(5)(4)}}{{298}}&=\displaystyle \frac{{(5.2)(3.7)}}{{{{T}_{2}}}}\\0.067&=\displaystyle \frac{{19.24}}{{{{T}_{2}}}}\\(0.067){{T}_{2}}&=19.24\\{{T}_{2}}&=287.16\text{ K}\end{align*}[/latex]
Check your answer: The pressure increases and the volume decreases, so the temperature will decrease.
Exercise 2.4
- A closed gas system initially has a volume of [latex]\scriptsize \displaystyle 8\text{ L}[/latex] and a temperature of [latex]\scriptsize 100\text{ }^\circ \text{C}[/latex]. The pressure of the gas is unknown. If the temperature of the gas decreases to [latex]\scriptsize 50\text{ }^\circ \text{C}[/latex], the gas occupies a volume of [latex]\scriptsize \displaystyle 5\text{ L}[/latex] and the pressure of the gas is [latex]\scriptsize \displaystyle 1.2\text{ atm}[/latex]. What was the initial pressure of the gas?
- [latex]\scriptsize \displaystyle 25\text{ c}{{\text{m}}^{\text{3}}}[/latex] of gas at [latex]\scriptsize \displaystyle 1\text{ atm}[/latex] has a temperature of [latex]\scriptsize 25\text{ }^\circ \text{C}[/latex]. When the gas is compressed to [latex]\scriptsize \displaystyle 20\text{ c}{{\text{m}}^{\text{3}}}[/latex], the temperature of the gas increases to [latex]\scriptsize 28\text{ }^\circ \text{C}[/latex]. Calculate the final pressure of the gas.
The full solutions can be found at the end of the unit.
Ideal gas law equation
In the early 1800s, Amedeo Avogadro noted that if you have samples of different gases, of the same volume, at a fixed temperature and pressure, then the samples must contain the same number of freely moving particles.
Avogadro’s law states that equal volumes of gases, at the same temperature and pressure, contain the same number of molecules.
The ideal gas law: the volume of a given amount of gas is directly proportional to the number of moles of gas, directly proportional to the temperature and inversely proportional to the pressure.
From the previous section, where we combined different gas law equations to get one that included temperature, volume, and pressure. In this equation:
[latex]\scriptsize \displaystyle \displaystyle \frac{{pV}}{T}=k[/latex] where the value of k is different for different masses of gas.
We find that when we calculate k for [latex]\scriptsize \displaystyle 1[/latex] mol of gas that we get:
[latex]\scriptsize \displaystyle \displaystyle \frac{{pV}}{T}=8.314[/latex]
This result is called the universal gas constant, R. R is measured in units of [latex]\scriptsize \displaystyle \text{J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}}[/latex]. No matter which gas we use, [latex]\scriptsize \displaystyle 1\text{ mol}[/latex] of that gas will have the same constant.
If we now extend this result to any number of moles of a gas, we get the following:
[latex]\scriptsize \displaystyle \displaystyle \frac{{pV}}{T}=nR[/latex]
where n is the number of moles of gas.
Rearranging this equation gives: [latex]\scriptsize \displaystyle pV=nRT[/latex]. This is the ideal gas equation.
All quantities in the equation [latex]\scriptsize \displaystyle pV=nRT[/latex] must be in the same units as the value of R. In other words, SI units must be used throughout the equation.
| Variable | SI Units | Other units |
| Pressure (p) | Pascals (Pa) | [latex]\scriptsize \displaystyle 760~\text{ mm Hg}=1~\text{ atm}=101~\text{ }325~\text{ Pa}=101.325\text{ }~\text{kPa}[/latex] |
| Volume (V) | [latex]\scriptsize \displaystyle {{\text{m}}^{\text{3}}}[/latex] | [latex]\scriptsize \displaystyle 1~{{\text{m}}^{\text{3}}}=1~\text{ }000~000~\text{ c}{{\text{m}}^{\text{3}}}=1~000~\text{ d}{{\text{m}}^{\text{3}}}=1~000\text{ }~\text{L}[/latex] |
| Moles (n) | mol | |
| Universal gas constant (R) | [latex]\scriptsize \displaystyle{\text{J}\text{.}{{\text{K}}^{{-1}}}\text{.mo}{{\text{l}}^{{-1}}}}[/latex] | |
| Temperature (K) | Kelvin (K) |
Example 2.11
Two moles of oxygen (O2) gas occupy a volume of [latex]\scriptsize \displaystyle 25\text{ d}{{\text{m}}^{\text{3}}}[/latex] at a temperature of [latex]\scriptsize 40\text{ }^\circ \text{C}[/latex]. Calculate the pressure of the gas under these conditions.
Solution
Step 1: List all the known information
Remember to convert the temperature to Kelvin and the volume to [latex]\scriptsize {{m}^{3}}[/latex] because the ideal gas equation must be used with SI units:
[latex]\scriptsize \displaystyle \begin{align*}p&=?\\V&=25~\text{ d}{{\text{m}}^{\text{3}}}=\displaystyle \frac{{25}}{{1000}}=0.025\text{ }{{\text{m}}^{3}}\\n&=2~\text{ mol}\\T&=40~\text{ }^\circ \text{C }=273+40=313\text{ K}\\R&=8.314~\text{ J}\text{.K}\text{.mo}{{\text{l}}^{{\text{-1}}}}\end{align*}[/latex]
Step 2: Choose the appropriate equation
Every component (pressure, temperature, and volume) is being varied so the correct equation to use is:
[latex]\scriptsize \displaystyle pV=nRT[/latex]
Step 3: Solve the equation
[latex]\scriptsize \displaystyle \begin{align*}(0,025~\text{ }{{\text{m}}^{\text{3}}})(p)&=(2~\text{ mol})(8.314~\text{ J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}})(313~\text{K})\\(0,025~\text{ }{{\text{m}}^{\text{3}}})(p)&=5~204.564~\text{Pa}\text{.}{{\text{m}}^{\text{3}}}\\p&=208~182.56~\text{Pa or 208}\text{.5 kPa}\end{align*}[/latex]
Example 2.12
Carbon dioxide (CO2) gas is produced as a result of the reaction between calcium carbonate and hydrochloric acid. The gas that is produced is collected in a container of unknown volume. The pressure of the gas is [latex]\scriptsize \displaystyle 105\text{ kPa}[/latex] at a temperature of [latex]\scriptsize 20\text{ }^\circ \text{C}[/latex]. If the number of moles of gas collected is[latex]\scriptsize \displaystyle 0.86\text{ mol}[/latex], what is the volume?
Solution
Step 1: List all known information, remembering to convert the required components to SI units
[latex]\scriptsize \displaystyle \begin{align*}p&=105~\text{ kPa}=105\text{ }x\text{ }1000=105000\text{ Pa}\\V&=?\\n&=0,86~\text{ mol}\\T&=20~\text{ }^\circ \text{C = 273 + 20 = 293 K}\\R&=8.314~\text{ J}\text{.K}\text{.mo}{{\text{l}}^{{\text{-1}}}}\end{align*}[/latex]
Step 2: Choose the appropriate equation
The temperature, pressure and volume is being varied so we will use:
[latex]\scriptsize \displaystyle pV=nRT[/latex]
Step 3: Solve the equation
[latex]\scriptsize \displaystyle \begin{align*}(105~000~\text{Pa})V&=(0,86~\text{ mol})(8,314~\text{ J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}})(293~\text{K})\\(105~000~\text{Pa})V&=2~094.96\text{ }~\text{Pa}\text{.}{{\text{m}}^{\text{3}}}\\V&=0,020~\text{ }{{\text{m}}^{\text{3}}}=20\text{ }~\text{d}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
Example 2.13
Nitrogen (N2) reacts with hydrogen (H2) according to the following equation:
[latex]\scriptsize \displaystyle {{\text{N}}_{2}}\text{+3}{{\text{H}}_{2}}\to \text{2N}{{\text{H}}_{3}}[/latex]
[latex]\scriptsize \displaystyle 2\text{ }mol[/latex] ammonia (NH3) gas is collected in a separate gas cylinder which has a volume of [latex]\scriptsize \displaystyle 25\text{ d}{{\text{m}}^{\text{3}}}[/latex]. The pressure of the gas is [latex]\scriptsize \displaystyle 195.89\text{ kPa}[/latex]. Calculate the temperature of the gas inside the cylinder.
Solution
Step 1: List the known information
Remember to convert the required components to SI units.
[latex]\scriptsize \displaystyle \begin{align*}p&=195.98~\text{ kPa}=195.98x1000=195\text{ }980\text{ Pa}\\V&=25~\text{ d}{{\text{m}}^{\text{3}}}=\displaystyle \frac{{25}}{{1000}}=0.025\text{ }{{\text{m}}^{\text{3}}}\\n&=2~\text{ mol}\\R&=8.3~14\text{J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{mo}{{\text{l}}^{{\text{-1}}}}\\T&=?\end{align*}[/latex]
Step 2: Choose the relevant gas law, substitute in the known values and solve
[latex]\scriptsize \displaystyle \begin{align*}pV&=nRT\\(195~890)(0,025)&=(2)(8,314)\text{T}\\4~897,25\text{T}&=16,628(\text{T})\\T&=294.52~\text{ K}\end{align*}[/latex]
Exercise 2.5
An unknown gas has a pressure of [latex]\scriptsize \displaystyle 112583.33\text{ Pa}[/latex], a temperature of [latex]\scriptsize 120\text{ }^\circ \text{C}[/latex] and the number of moles is [latex]\scriptsize \displaystyle 0.28\text{ mol}[/latex]. What is the volume of the sample?
A learner is asked to calculate the answer to the problem below:
Calculate the pressure exerted by [latex]\scriptsize \displaystyle 1.5\text{ moles}[/latex] of nitrogen gas in a container with a volume of [latex]\scriptsize \displaystyle 20\text{ d}{{\text{m}}^{\text{3}}}[/latex] at a temperature of [latex]\scriptsize \displaystyle 37\text{ }^\circ \text{C}[/latex].
The learner writes the solution as follows:
[latex]\scriptsize \displaystyle \begin{align*}n&=1.5\text{ mol}\\V&=20\text{ d}{{\text{m}}^{\text{3}}}\\T&=\text{37}+\text{273}=\text{310 }\!\!~\!\!\text{ K}\\R&=8.314\text{ J}\text{.}{{\text{K}}^{{-1}}}\text{.mo}{{\text{l}}^{{-1}}}\\pT&=nRV\\p(310)&=(1,5)(8,314)(20)\\p(310)&=249.42\\p&=0.8~\text{kPa}\end{align*}[/latex]
Identify two mistakes which were made.
The full solutions can be found at the end of the unit.
Note
To consolidate your understanding of the gas laws you can watch this video by Professor Dave. Whilst watching this video, please note that the pressure is stated in atm’s so the value of the constant is different to the one used in this unit.
Note
To further understand how to use each gas law and which law to use watch this video. Whilst watching this video, please note that the pressure is stated in atm’s so the value of the constant is different to the one used in this unit.
Summary
In this unit you have learnt the following:
- An ideal gas has identical particles of zero volume, with no intermolecular forces between the particles. The atoms or molecules in an ideal gas move at the same speed.
- A real gas behaves like an ideal gas, except at high pressures and low temperatures. At low temperatures, the forces between molecules become significant and the gas will liquefy. At high pressures, the volume of the particles becomes significant.
- Boyle’s law states that the pressure of a fixed quantity of gas is inversely proportional to the volume it occupies so long as the temperature remains constant. In other words, [latex]\scriptsize \displaystyle pV=k[/latex] or [latex]\scriptsize \displaystyle {{p}_{1}}{{V}_{1}}={{p}_{2}}{{V}_{2}}[/latex].
- Charles’s law states that the volume of an enclosed sample of gas is directly proportional to its Kelvin temperature provided the pressure and amount of gas remains constant. In other words, [latex]\scriptsize \displaystyle \displaystyle \frac{V}{T}=k[/latex] or [latex]\scriptsize \displaystyle \displaystyle \frac{{{{V}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{V}_{2}}}}{{{{T}_{2}}}}[/latex].
- The pressure of a fixed mass of gas is directly proportional to its temperature if the volume is constant. In other words, [latex]\scriptsize \displaystyle \displaystyle \frac{p}{T}=k[/latex] or [latex]\scriptsize \displaystyle \displaystyle \frac{{{{p}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{p}_{2}}}}{{{{T}_{2}}}}[/latex].
- For Charles’s law and for the pressure-temperature relation, the temperature must be written in Kelvin. Temperature in degrees Celsius (℃) can be converted to temperature in Kelvin (K) using the following equation: [latex]\scriptsize \displaystyle TK=T{{\text{ }}^{o}}C+273[/latex].
- Combining Boyle’s law and the relationship between the temperature and pressure of a gas, gives the general gas equation, which applies as long as the amount of gas remains constant. The general gas equation is [latex]\scriptsize \displaystyle \displaystyle \frac{{pV}}{T}=k[/latex] or [latex]\scriptsize \displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}=\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}[/latex].
- Avogadro’s law states that equal volumes of gases, at the same temperature and pressure, contain the same number of molecules.
- The universal gas constant (R) is [latex]\scriptsize \displaystyle 8.314\text{ J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}}[/latex]. This constant is found by calculating [latex]\scriptsize \displaystyle \frac{{pV}}{T}[/latex] for [latex]\scriptsize \displaystyle 1\text{ mol}[/latex] of any gas.
- Extending the above calculation to apply to any number of moles of gas gives the ideal gas equation: [latex]\scriptsize \displaystyle pV=nRT[/latex].
- In this equation, SI units must be used. The SI unit for volume is [latex]\scriptsize \displaystyle {{\text{m}}^{\text{3}}}[/latex], for pressure it is [latex]\scriptsize \displaystyle \text{Pa}[/latex] and for temperature it is K.
Unit 2: Assessment
Suggested time to complete: 30 minutes
- Give one word or term for each of the following definitions:
- A gas that has identical particles of zero volume, with no intermolecular forces between the particles.
- The law that states that the volume of a gas is directly proportional to the temperature of the gas, provided that the pressure and the amount of the gas remain constant.
- A measure of the average kinetic energy of gas particles.
- Which one of the following properties of a fixed quantity of a gas must be kept constant during an investigation of Boyle’s law?
- density
- pressure
- temperature
- volume
- Three containers of equal volume are filled with equal masses of helium, nitrogen, and carbon dioxide gas, respectively. The gases in the three containers are all at the same temperature. Which one of the following statements is correct regarding the pressure of the gases?
- All three gases will be at the same pressure.
- The helium will be at the greatest pressure.
- The nitrogen will be at the greatest pressure.
- The carbon dioxide will be at the greatest pressure.
- The ideal gas equation is given by [latex]\scriptsize \displaystyle pV=nRT[/latex]. Which one of the following conditions is true according to Avogadro’s Law?
a [latex]\scriptsize \displaystyle p\propto V~~~~[/latex](T = constant) b [latex]\scriptsize \displaystyle V\propto T[/latex] (p = constant) c [latex]\scriptsize \displaystyle V\propto n[/latex] (p, T = constant) d [latex]\scriptsize \displaystyle p\propto T[/latex] (n = constant) - Use your knowledge of the gas laws to explain the following statements:
- It is dangerous to put an aerosol can near heat.
- A pressure vessel that is poorly designed and made can be a serious safety hazard (a pressure vessel is a closed, rigid container that is used to hold gases at a pressure that is higher than the normal air pressure).
- The volume of a car tyre increases after a trip on a hot road.
- One of the cylinders of a motor car engine, before compression contains [latex]\scriptsize \displaystyle 450\text{ c}{{\text{m}}^{\text{3}}}[/latex] of a mixture of air and petrol in the gaseous phase, at a temperature of [latex]\scriptsize 30\text{ }^\circ \text{C}[/latex] and a pressure of [latex]\scriptsize \displaystyle 100\text{ kPa}[/latex]. If the volume of the cylinder after compression decreases to one tenth of the original volume, and the temperature of the gas mixture rises to [latex]\scriptsize \displaystyle 140\text{ }^\circ \text{C}[/latex], calculate the pressure now exerted by the gas mixture.
- A gas of unknown volume has a temperature of [latex]\scriptsize 14\text{ }^\circ \text{C}[/latex]. When the temperature of the gas is increased to [latex]\scriptsize \displaystyle 100\text{ }^\circ \text{C}[/latex], the volume is found to be [latex]\scriptsize \displaystyle 5.5\text{ L}[/latex]. What was the initial volume of the gas?
- An average pair of human lungs contains about [latex]\scriptsize \displaystyle 3.5\text{ L}[/latex] of air after inhalation and about [latex]\scriptsize \displaystyle 3.0\text{ L}[/latex] after exhalation. Assuming that air in your lungs is at [latex]\scriptsize 37\text{ }^\circ \text{C}[/latex] and [latex]\scriptsize \displaystyle 1.0\text{ atm}[/latex], determine the number of moles of air in a typical breath.
The full solutions can be found at the end of the unit.
Unit 2: Solutions
Exercise 2.1
- .
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{2}}{{V}_{2}}&={{p}_{1}}{{V}_{1}}\\1.5~\text{L}{{p}_{2}}&=(150~\text{kPa})(1~\text{L})\\{{p}_{2}}&=\displaystyle \frac{{150}}{{1.5}}\\&=100~\text{kPa}\end{align*}[/latex]
The volume has increased, so the pressure will decrease. - .
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{2}}{{V}_{2}}&={{p}_{1}}{{V}_{1}}\\200\text{ c}{{\text{m}}^{3}}{{p}_{2}}&=(90~\text{kPa})(250~\text{c}{{\text{m}}^{\text{3}}})\\200\text{ c}{{\text{m}}^{\text{3}}}{{p}_{2}}&=22~500~\text{kPa}\\{{p}_{2}}&=\displaystyle \frac{{22500}}{{200}}\\&=112.5~\text{kPa}\end{align*}[/latex]
The volume is reduced so the pressure will increase. - .
[latex]\scriptsize \displaystyle \begin{align*}{{p}_{2}}{{V}_{2}}&={{p}_{1}}{{V}_{1}}\\120~\text{kPa}{{V}_{2}}&=(100~\text{kPa})(10~\text{c}{{\text{m}}^{\text{3}}})\\{{V}_{2}}&=\displaystyle \frac{{1000}}{{120}}\\&=8.33~\text{c}{{\text{m}}^{\text{3}}}\end{align*}[/latex]
The pressure has increased so the volume will be reduced.
Exercise 2.2
- .
[latex]\scriptsize \displaystyle \begin{align*}{{V}_{1}}&=623\text{ mL}\\{{T}_{1}}&=\text{ }255\text{ }\!\!^\circ\!\!\text{ C = 273+ 255 = 528 K}\\{{V}_{2}}&=\text{ }277\text{ mL}\\{{T}_{2}}&=\displaystyle \frac{{{{V}_{2}}\text{x}{{T}_{1}}}}{{{{V}_{1}}}}\\{{T}_{2}}&=\displaystyle \frac{{277\text{x}528}}{{623}}=234.76\text{ K}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=8+273=281\text{ K}\\{{T}_{2}}&=25+273=298\text{ K}\\{{V}_{1}}&=4.4\text{ d}{{\text{m}}^{3}}\\{{V}_{2}}&=\displaystyle \frac{{{{V}_{1}}x{{T}_{2}}}}{{{{T}_{1}}}}\\{{V}_{2}}&=\displaystyle \frac{{4.4x298}}{{281}}\\{{V}_{2}}&=4.67\text{ d}{{\text{m}}^{3}}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{V}_{2}}&=200\text{ c}{{\text{m}}^{\text{3}}}=\displaystyle \frac{{200}}{{1000}}=0.2\text{ d}{{\text{m}}^{3}}\\{{V}_{1}}&=1.2\text{ d}{{\text{m}}^{3}}\\{{T}_{1}}&=340\text{ K}\\{{T}_{2}}&=?\\{{T}_{2}}&=\displaystyle \frac{{{{V}_{2}}\text{x}{{T}_{1}}}}{{{{V}_{1}}}}\\{{T}_{2}}&=\displaystyle \frac{{0.2\text{x}340}}{{1.2}}\\{{T}_{2}}&=56.67\text{ K}\end{align*}[/latex]
Exercise 2.3
- .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=15+273=288\text{ K}\\{{T}_{{_{2}}}}&=25+273=298\text{ K}\\{{p}_{1}}&=7\text{ atm}\\{{p}_{2}}&=?\text{ atm}\\\displaystyle \frac{{{{p}_{2}}}}{{{{T}_{2}}}}&=\displaystyle \frac{{{{p}_{1}}}}{{{{T}_{1}}}}\\\displaystyle \frac{{{{p}_{2}}}}{{298}}&=\displaystyle \frac{7}{{288}}\\\displaystyle \frac{{{{p}_{2}}}}{{298}}&=0.024\\{{p}_{2}}&=7.24\text{ atm}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=8\text{ K}\\{{T}_{2}}&=?\text{ K}\\{{p}_{1}}&=5\text{ atm}\\{{p}_{2}}&=291\text{ atm}\\\displaystyle \frac{{{{p}_{1}}}}{{{{p}_{2}}}}&=\displaystyle \frac{{{{T}_{1}}}}{{{{T}_{2}}}}\\\displaystyle \frac{5}{{291}}&=\displaystyle \frac{8}{{{{T}_{2}}}}\\0.0017&=\displaystyle \frac{8}{{{{T}_{2}}}}\\(0.0017){{T}_{2}}&=8\\{{T}_{2}}&=465.6\text{ K}\end{align*}[/latex]
Exercise 2.4
- .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=100+273=373~\text{K}\\{{T}_{2}}&=50+273=323~\text{K}\\{{p}_{1}}&=?\\{{p}_{2}}&=1.2\text{ atm}\\{{V}_{1}}&=8\text{ L}\\{{V}_{2}}&=5\text{ L}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}\displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}&=\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}\\\displaystyle \frac{{{{p}_{1}}(8)}}{{373}}&=\displaystyle \frac{{(1.2)(5)}}{{323}}\\\displaystyle \frac{{{{p}_{1}}(8)}}{{373}}&=0.0185\\({{p}_{1}})(8)&=6.928\\{{p}_{1}}&=0.87\text{ atm}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=25+273=298~\text{K}\\{{T}_{2}}&=28+273=301~\text{K}\\{{p}_{1}}&=1\text{ atm}\\{{p}_{2}}&=?\\{{V}_{1}}&=25\text{ c}{{\text{m}}^{3}}\\{{V}_{2}}&=20\text{ c}{{\text{m}}^{3}}\\\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}&=\displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}\\\displaystyle \frac{{{{p}_{2}}(20)}}{{301}}&=\displaystyle \frac{{(1)(25)}}{{298}}\\\displaystyle \frac{{{{p}_{2}}(20)}}{{301}}&=0.08389\\({{p}_{2}})(20)&=25.516\\{{p}_{2}}&=1.26\text{ atm}\end{align*}[/latex]
Exercise 2.5
- .
[latex]\scriptsize \displaystyle \begin{align*}T&=120\text{ }^\circ \text{C = 273+120 = 393 }K\\V&=?\\p&=112583.33Pa\\n&=0.28\text{ }mol\\R&=8.314\text{ }J.{{K}^{{-1}}}mo{{l}^{{-1}}}\end{align*}[/latex]
[latex]\scriptsize \displaystyle \begin{align*}pV&=nRT\\(112~583.33)V&=(0.28)(8.314)(393)\\(112583.33)V&=895\text{ }7256\\V&=0.008~\text{ }{{\text{m}}^{\text{3}}}=8~\text{ d}{{\text{m}}^{\text{3}}}\end{align*}[/latex] - The learner has not used the correct equation. The ideal gas equation is [latex]\scriptsize \displaystyle pV=nRT[/latex].
The learner did not convert the volume to SI units.
Unit 2: Assessment
- .
- Ideal gas
- Charles’s law
- Temperature
- c. Temperature must be kept constant.
- b. The sample of helium gas will be at the greatest pressure. Helium is the smallest, in terms of atomic mass, which means there will be more helium particles in the container, leading to more collisions so the pressure will be the highest.
- c. [latex]\scriptsize \displaystyle V\propto n[/latex], with p, T constant.
- .
- As the temperature of a gas increases the pressure also increases (provided the volume stays constant). Since the volume of an aerosol can stays constant, the pressure will increase and cause the can to explode.
- As the temperature of a gas increases the pressure also increases (provided the volume stays constant). Since the volume of a pressure vessel stays constant, the pressure will increase if the temperature increases and cause the vessel to explode. Also, since the vessel keeps the gas at a higher pressure than normal, the gas is more likely to burst out of the container.
- Volume is proportional to temperature at a fixed pressure. The pressure of a car tyre is fixed. After a long trip, the temperature of the tyre increases which leads to an increase in the volume.
- .
[latex]\scriptsize \displaystyle \begin{align*}{{T}_{1}}&=30\text{ }^\circ \text{C = }273+30=303\text{ K}\\{{T}_{2}}&=140\text{ }^\circ \text{C}=273+140=413\text{ K}\\{{V}_{1}}&=450\text{ c}{{\text{m}}^{\text{3}}}=\displaystyle \frac{{450}}{{1000}}=0.450\text{ }{{\text{m}}^{\text{3}}}\\{{V}_{2}}&=\displaystyle \frac{1}{{10}}{{V}_{1}}=0.0450\text{ }{{\text{m}}^{\text{3}}}\\{{p}_{1}}&=100\text{ kPa}=100000\text{ Pa}\\{{p}_{2}}&=?\\\displaystyle \frac{{{{p}_{2}}{{V}_{2}}}}{{{{T}_{2}}}}&=\displaystyle \frac{{{{p}_{1}}{{V}_{1}}}}{{{{T}_{1}}}}\\\displaystyle \frac{{{{p}_{2}}(0.0450)}}{{413}}&=\displaystyle \frac{{(100000)(0.450)}}{{303}}\\\displaystyle \frac{{{{p}_{2}}(0.0450)}}{{413}}&=148.52\\{{p}_{2}}(0.0450)&=61336.6\\{{p}_{2}}&=1363036.3\text{ Pa}=1363.0\text{ kPa}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{T}_{1}}&=14+273=287\text{ K}\\{{T}_{2}}&=100+273=373\text{ K}\\{{V}_{1}}&=?\\{{V}_{2}}&=5.5\text{ L}\\\displaystyle \frac{{{{V}_{1}}}}{{{{T}_{1}}}}&=\displaystyle \frac{{{{V}_{2}}}}{{{{T}_{2}}}}\\\displaystyle \frac{{{{V}_{1}}}}{{287}}&=\displaystyle \frac{{5.5}}{{373}}\\\displaystyle \frac{{{{V}_{1}}}}{{287}}&=0.020\\{{V}_{1}}&=5.74\text{ L}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}V&=3.5\text{ L}-3.0\text{ L}=0.0005\text{ }{{\text{m}}^{\text{3}}}\\T&=37+273=310\text{ K}\\p&=101325\text{ Pa}\\n&=?\\R&=8.314\text{ J}\text{.}{{\text{K}}^{{\text{-1}}}}\text{.mo}{{\text{l}}^{{\text{-1}}}}\\pV&=nRT\\(101325)(0.0005)&=n(8.314)(310)\\50.6625&=(n)(2577.34)\\n&=0.02\text{ mol}\end{align*}[/latex]
Media Attributions
- Fig 1 © Nadina Wiokiewicpzi is licensed under a CC BY-SA (Attribution ShareAlike) license
- Fig 2 © Libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 4 © DHET is licensed under a CC BY (Attribution) license
- Fig 5 © NASA is licensed under a Public Domain license
- Fig 6 © Libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 7 © Siyavula is licensed under a CC BY-ND (Attribution NoDerivatives) license
- Fig 8 © Libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 9 © DHET is licensed under a CC BY (Attribution) license
- Fig 10 © Libretext is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Fig 11 © Siyavula is licensed under a CC BY-ND (Attribution NoDerivatives) license
a continuous physical force exerted on or against an object by something in contact with it
force per unit area exerted by the mass of the atmosphere as gravity pulls it to Earth
the pressure relative to atmospheric pressure
pressure of a fixed mass of gas is inversely proportional to volume at a constant temperature
variables which one variable decreases with the increase in another variable and one variable increases with the decrease in another variable.
the volume of an enclosed sample of gas is directly proportional to its Kelvin temperature provided the pressure and amount of gas is kept constant
