Mechanics: Describe, analyse and apply principles of simple machines and mechanical advantage
Unit 1: The mechanical advantage of an inclined plane
Leigh Kleynhans
Unit outcomes
By the end of this unit you will be able to:
- Describe, identify, and calculate the mechanical advantage of inclined planes.
What you should know
Before you start this unit, make sure you can:
- Identify an inclined plane as a simple machine.
Introduction
In this unit you will build on your knowledge of simple machines and forces to understand how an inclined plane offers . You will also learn how to calculate the mechanical advantage of an .
Inclined planes are often used when heavy objects need to be moved to a higher vertical position. Instead of lifting the object up, it can be pushed up a ramp. There are many examples in everyday life where ramps are used to make a task easier.
How inclined planes create a mechanical advantage
For an inclined plane, less force is put into moving an object up the slope than if the object were lifted straight up, so the mechanical advantage will be greater than [latex]\scriptsize 1[/latex]. The more gradual the slope of the inclined plane, the less input force is needed and the greater the mechanical advantage.
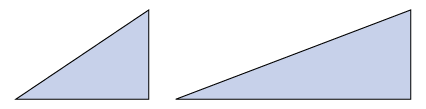
The inclined plane on the right has a more gradual slope, so it has a greater mechanical advantage. Less force is needed to move objects up the gentler slope, yet the objects attain the same height as they would if more force were used to push them up the steeper slope on the left.
There is a trade-off with this simple machine. If the slope is gentle, a person has to push or pull the object over a longer distance, but with little effort. If the slope is steep, a person has to push or pull the object over a very short distance, but with more effort.
Activity 1.1: Investigate the mechanical advantage of an inclined plane
What you need:
- small rocks
- a sandwich bag
- a stack of books
- a spring balance (If you do not have a spring balance watch the video link at the end of the activity)
- a ruler
- a flat piece of wood of minimum length [latex]\scriptsize 1\text{ m}[/latex]
What to do:
- Fill the sandwich bag with rocks and seal the bag.
- Attach the hook of the spring balance through the top of the sandwich.
- Lift the bag vertically and read the force required to lift the bag to a height of [latex]\scriptsize 30\text{ cm}[/latex].
- Place one end of the flat piece of wood on the stack of books of height [latex]\scriptsize 30\text{ cm}[/latex] to make an inclined plane.
- Drag the bag of rocks, using the spring balance up the slope and measure the force required.
What did you find?
The force required to lift the bag of rocks vertically is greater than the force required to drag it up the slope. The inclined plane reduced the required effort force to raise the bag of rocks to a height of [latex]\scriptsize 30\text{ cm}[/latex].
Note
If you do not have access to a spring balance, you can watch a video of this experiment online.
Calculating mechanical advantage of inclined planes
To lift an object vertically, the force required would be equal to the weight of the object. ([latex]\scriptsize {{F}_{g}}=mg[/latex]) and the object will gain gravitational potential energy ([latex]\scriptsize {{E}_{p}}=mgh[/latex]). Level 2 Subject Outcome 2.2 Unit 3 and Level 2 Subject Outcome 2.3 Unit 1
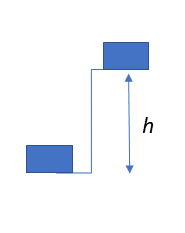
To push an object up a frictionless inclined plane, the force would be the effort (Fe) exerted over the distance up the plane. ([latex]\scriptsize W={{F}_{e}}L[/latex]). However, the gain in would still be the same ([latex]\scriptsize {{E}_{p}}=mgh[/latex]).

Therefore:
[latex]\scriptsize \begin{align*}mgh&={{F}_{e}}L\\{{F}_{g}}h&={{F}_{e}}L\end{align*}[/latex]
and the ideal mechanical advantage ([latex]\scriptsize IMA[/latex]) can be expressed as [latex]\scriptsize \displaystyle \frac{{{{F}_{e}}}}{{{{F}_{e}}}}\text{ or }\displaystyle \frac{L}{h}[/latex].
As heights and lengths can be easily measured, the following formula is most commonly used to calculate the ideal mechanical advantage of an inclined plane:
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}\text{ where: }L\text{ is the length of the plane and }h\text{ is the vertical height}[/latex]
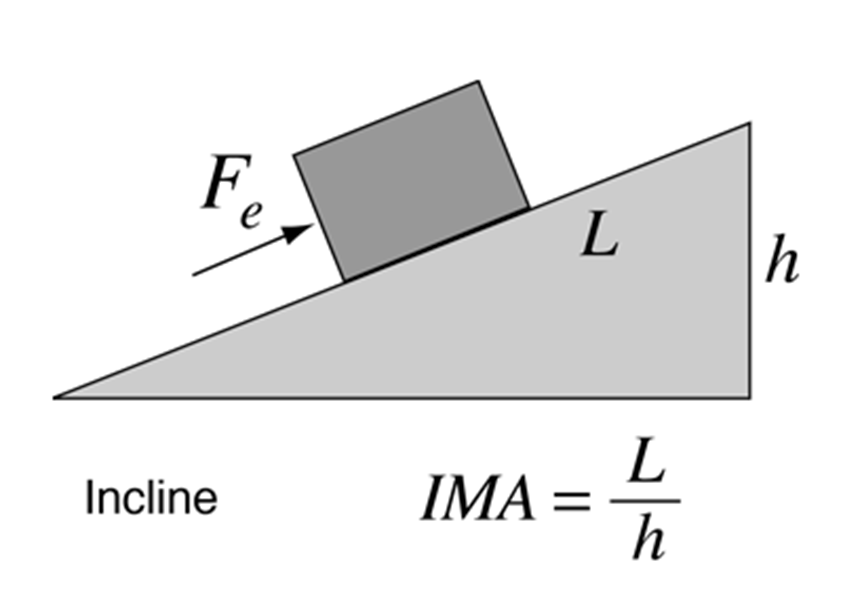
In reality, there will always be some energy ‘lost’ in overcoming friction when objects are pushed over surfaces.
Example 1.1
Calculate the ideal mechanical advantage of using a frictionless ramp of length [latex]\scriptsize 4\text{ m}[/latex] to raise a box to a platform with a vertical height of [latex]\scriptsize 2.5\text{ m}\text{.}[/latex]
Solution
Step 1: Write the formula
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}[/latex]
Step 2: Substitute the values and do the calculation
[latex]\scriptsize \displaystyle \frac{4}{{2.5}}=1.6[/latex]
Note: there are no units for mechanical advantage.
Note
To consolidate your understanding, you can watch this video to see the mechanical advantage of an inclined plane when loading a box into the back of a van.
Summary
- An inclined plane is a simple machine that consists of a sloping surface connecting a lower elevation to a higher elevation. It is used to move objects more easily to the higher elevation.
- Less force is needed to move an object uphill with an inclined plane, but the force must be applied over a greater distance.
- The mechanical advantage of an inclined plane is always greater than [latex]\scriptsize 1[/latex] because the machine puts out more force than the user puts into it.
- The ideal mechanical advantage of a frictionless inclined plane can be calculated using the formula: [latex]\scriptsize IMA=\displaystyle \frac{L}{h}[/latex].
Unit 1: Assessment
Suggested time to complete: 15 minutes
- Explain how inclined planes act as simple machines.
- The mechanical advantage of an inclined plane can be increased by:
- shortening the path of the incline
- enlarging the angle of the incline
- minimising the angle of the incline
- reducing the force used to move objects
- Calculate the ideal mechanical advantage of using the following frictionless inclined planes:
- .
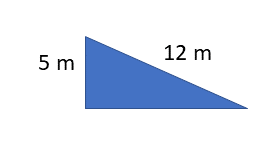
- .
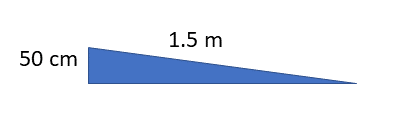
- .
- Calculate the ideal mechanical advantage of using the following frictionless inclined planes:
- .

- .

- .
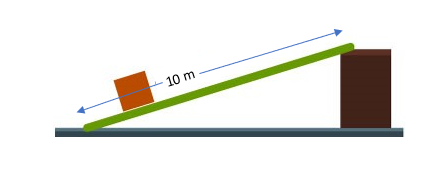
- What is the height of the platform illustrated below if the ideal mechanical advantage provided by the ramp is 6?
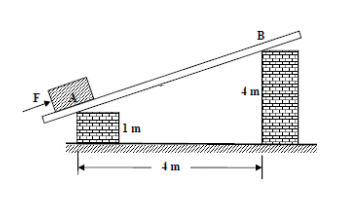
- A learner pushes an object with a force of F from point A to point B, as shown in the figure below. If the friction between object and board is ignored, determine the mechanical advantage.
- Name three situations in everyday life where inclined planes are used.
The full solutions are at the end of the unit.
Unit 1: Solutions
Unit 1: Assessment
- Inclined planes reduce the force required to move an object up to a higher level by increasing the distance over which the force acts.
- C (minimising the angle of inclination)
.
Here is an explanation:
.
The equation of mechanical advantage of the inclined plane is as follows:
.
Mechanical advantage = length of inclined plane/height of the inclined plane- The mechanical advantage is directly proportional to the length of the inclined plane and therefore the mechanical advantage is enlarged if the length of the incline is enlarged.
- The mechanical advantage is inversely proportional to the height of the inclined plane; therefore, the mechanical advantage is minimised if the height of the inclined plane is enlarged and the mechanical advantage is enlarged if the height of the incline is reduced.
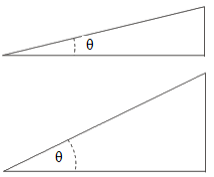
- If the angle is minimised then the height of the inclined plane is reduced. The mechanical advantage is enlarged if the height of the inclined plane is reduced. Hence if the angle is minimised then the mechanical advantage is enlarged.
- If the angle is enlarged then the height of the inclined plane is enlarged. The mechanical advantage is minimised if the height of the inclined plane is enlarged. Hence if the angle is enlarged then the mechanical advantage is minimized.
- .
- [latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{12}}{5}=2.4[/latex]
- [latex]\scriptsize 50\text{ cm = 0}\text{.5 m}[/latex]
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{1.5}}{{0.5}}=3[/latex]
- .
- Use Pythagoras to find [latex]\scriptsize L[/latex]:
[latex]\scriptsize \begin{align*}{{L}^{2}}&={{2}^{2}}+{{6}^{2}}\\L&=6.32\text{ m}\end{align*}[/latex]
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{6.32}}{2}=3.16[/latex] - Use Pythagoras to find [latex]\scriptsize h[/latex]:
[latex]\scriptsize \begin{align*}{{7}^{2}}&={{5}^{2}}+{{h}^{2}}\\h&=4.9\text{ m}\end{align*}[/latex]
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{{4.9}}{2}=2.45[/latex]
- Use Pythagoras to find [latex]\scriptsize L[/latex]:
- .
[latex]\scriptsize \begin{align*}IMA&=\displaystyle \frac{L}{h}\\\text{ }6&=\displaystyle \frac{{10}}{h}\\\text{ }h&=\text{1}\text{.67 m}\end{align*}[/latex] - Height of inclined plane [latex]\scriptsize =4-1=3\text{ m}[/latex]
Length of horizontal plane [latex]\scriptsize 4\text{ m}[/latex]
Use Pythagoras to calculate length of the inclined plane:
[latex]\scriptsize \begin{align*}{{L}^{2}}&={{3}^{2}}+{{4}^{2}}\\L&=5\text{ m}\end{align*}[/latex]
[latex]\scriptsize IMA=\displaystyle \frac{L}{h}=\displaystyle \frac{5}{3}=1.67[/latex] - .
- loading ramps
- wheelchair ramps
- stairs
- escalators
- inclined conveyor belts
- ladders
- roads to high elevations
- or any other appropriate examples.
Media Attributions
- img01_Figure1 © DHET is licensed under a CC BY (Attribution) license
- img02_Figure2 © DHET is licensed under a CC BY (Attribution) license
- img03_Figure3 © DHET is licensed under a CC BY (Attribution) license
- img04_Figure4 © DHET is licensed under a CC BY (Attribution) license
- img05_AssessmentQ3 © DHET is licensed under a CC BY (Attribution) license
- img05_AssessmentQ3 © DHET is licensed under a CC BY (Attribution) license
- img06_AssesssmentQ4 © DHET is licensed under a CC BY (Attribution) license
- img06_AssesssmentQ4 © DHET is licensed under a CC BY (Attribution) license
- img07_AssessmentQ5_2 © DHET is licensed under a CC BY (Attribution) license
- img08_AssessmentQ6 © DHET is licensed under a CC BY (Attribution) license
- img09_AssessmentQ2answer © DHET is licensed under a CC BY (Attribution) license
how a simple machine can reduce the force required to move an object
a surface that is raised on one side forming a slope
the energy that an object possesses because of its vertical height above the ground
