Mechanics: State, explain and interpret principles of horizontal motion
Unit 1: Linear equations of motion
Dylan Busa
Unit outcomes
By the end of this unit you will be able to:
- Analyse and calculate more complex problems, using linear equations of motion:
- [latex]\scriptsize {{v}_{f}}={{v}_{i}}+a\Delta t[/latex]
- [latex]\scriptsize s={{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}[/latex]
- [latex]\scriptsize v_{f}^{2}=v_{i}^{2}+2as[/latex].
What you should know
Before you start this unit, make sure you can:
- Explain the difference between displacement and distance. See level 2 subject outcome 2.1 unit 1 if you need help with this.
- Calculate speed and average velocity and acceleration. See level 2 subject outcome 2.1 unit 1 if you need help with this.
- Use simple linear equations of motion to predict the outcome of motion of a body. See level 2 subject outcome 2.1 unit 2 if you need help with this.
- Explain the difference between a scalar and a vector. See level 2 subject outcome 2.1 unit 3 if you need help with this.
- Determine the overall result of two or more vectors in two dimensions using a scale diagram. See level 2 subject outcome 2.1 unit 4 if you need help with this.
Introduction
In level 2 subject outcome 2.1 we learnt about the basic equations of motion that help us calculate and predict the motion of moving objects. These equations are as follows:
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}&={{v}_{i}}+a\Delta t &&\text{equation 1}\\s &={{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}} &&\text{equation 2}\\v_{f}^{2}&=v_{i}^{2}+2as &&\text{equation 3}\end{align*}[/latex]
Where:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=\text{initial velocity (in m}\text{.}{{\text{s}}^{{-1}}})\\{{v}_{f}}&=\text{final velocity (in m}\text{.}{{\text{s}}^{{-1}}})\\a&=\text{acceleration (in m}\text{.}{{\text{s}}^{{-2}}})\\s&=\text{ displacement/distance in a straight line (in m})\\\Delta t&=\text{time (in s)}\end{align*}[/latex]
Thankfully, these equations do not need to be learnt off by heart. In the examination, they will be given to you on a data sheet. Each equation has four variables. You will need any three known quantities to be able to calculate the fourth unknown one.
It is very important to keep in mind that these equations only work for:
- motion that is in one dimension (i.e. for bodies that are travelling in a straight line)
- objects that are under constant acceleration.
In this unit you will apply your knowledge about the equations of motion to analyse and solve more complex problems. You will also see how these apply in real-world situations and so expand your understanding of the effects of velocity, displacement and acceleration in everyday applications.
Problem-solving strategy
The following strategy for solving linear motion problems is adapted from 2.6 Problem-Solving Basic for One-Dimensional Kinematics by OpenStax Physics.
Step 1: Read the question carefully and draw a sketch
Carefully read the question and the situation it describes to determine which physical principles are involved. It often helps to draw a simple sketch at the outset. You will also need to decide which direction is positive and note that on your sketch. Once you have identified the physical principles, it is much easier to find and apply the equations representing those principles.
Step 2: Identify the known facts and variables
Identify the knowns by making a list of what is given or can be inferred from the problem as stated. Many problems are stated succinctly and require some interpretation to determine what is known. Again, a sketch can also be very useful at this point. Remember the following:
- If an object ‘starts from rest’, then [latex]\scriptsize {{v}_{i}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- If an object ‘comes to rest’ OR stops, then [latex]\scriptsize {{v}_{f}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- Slowing down means acceleration is negative while still moving in a positive direction.
- Constant velocity means [latex]\scriptsize \displaystyle a=0\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex], [latex]\scriptsize {{v}_{i}}={{v}_{f}}[/latex] and you can use [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}[/latex].
Step 3: Identify what needs to be found
Identify exactly what needs to be determined. In more complex problems it is not always obvious what needs to be found or in what sequence, but making a list can help.
Step 4: Find an equation that helps solve the problem
Find an equation or set of equations that can help you solve the problem. Your list of knowns and unknowns can help here. Look for equations that contain only one unknown.
If an equation contains more than one unknown, then an additional equation is needed to solve the problem. In some problems, several unknowns must be determined to solve for the targeted one.
Step 5: Substitute the knowns into the equations(s)
Substitute the knowns along with their units into the appropriate equation, and obtain numerical solutions complete with units.
Using this step to check on units can help you find errors. If the units of the answer are incorrect, then an error has been made.
Step 6: Check your answer
Check the answer to see if it is reasonable. To see if the answer is reasonable, check both its magnitude and its sign, as well as its units. Here is an example:
If a person starts a race on foot and accelerates at [latex]\scriptsize 0.40\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] for [latex]\scriptsize 100\text{ s}[/latex] what would his final velocity be? To solve this, we would use equation 1 noted above.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}&={{v}_{i}}+a.\Delta t\\&=0+0.40\text{ m}\text{.}{{\text{s}}^{{-2}}}\times 100\text{ s}\\&=40\text{ m}\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex]
Now the mathematical calculation is correct but does the answer make sense in the real world. How fast is [latex]\scriptsize 40\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]?
[latex]\scriptsize \begin{align*}&\displaystyle \frac{{40\text{ m}\text{.}{{\text{s}}^{{-1}}}}}{{1\ 000\text{ m}\text{.k}{{\text{m}}^{{-1}}}}}\times 3\ 600\text{ s}\text{.}{{\text{h}}^{{-1}}}\\&=144\text{ km/h}\end{align*}[/latex]
Clearly, it is not possible for a runner to achieve this speed so one of the values we substituted into the equation of motion was wrong. We would need to go back and determine where the mistake had come from.
Use equations of motion to solve problems
Let’s look at some worked examples of these six steps.
Example 1.1
An airplane lands with an initial velocity of [latex]\scriptsize 70\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] and then decelerates at [latex]\scriptsize 1.50\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] for [latex]\scriptsize 40\text{ s}[/latex]. What is its final velocity?
Solution
In this situation the acceleration is not zero but it is a constant negative [latex]\scriptsize 1.50\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. We have been given an initial velocity of [latex]\scriptsize 70\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] and asked to find the final velocity after [latex]\scriptsize 40\text{ s}[/latex]. Because [latex]\scriptsize a\ne 0[/latex], [latex]\scriptsize {{v}_{f}}\ne {{v}_{i}}[/latex].
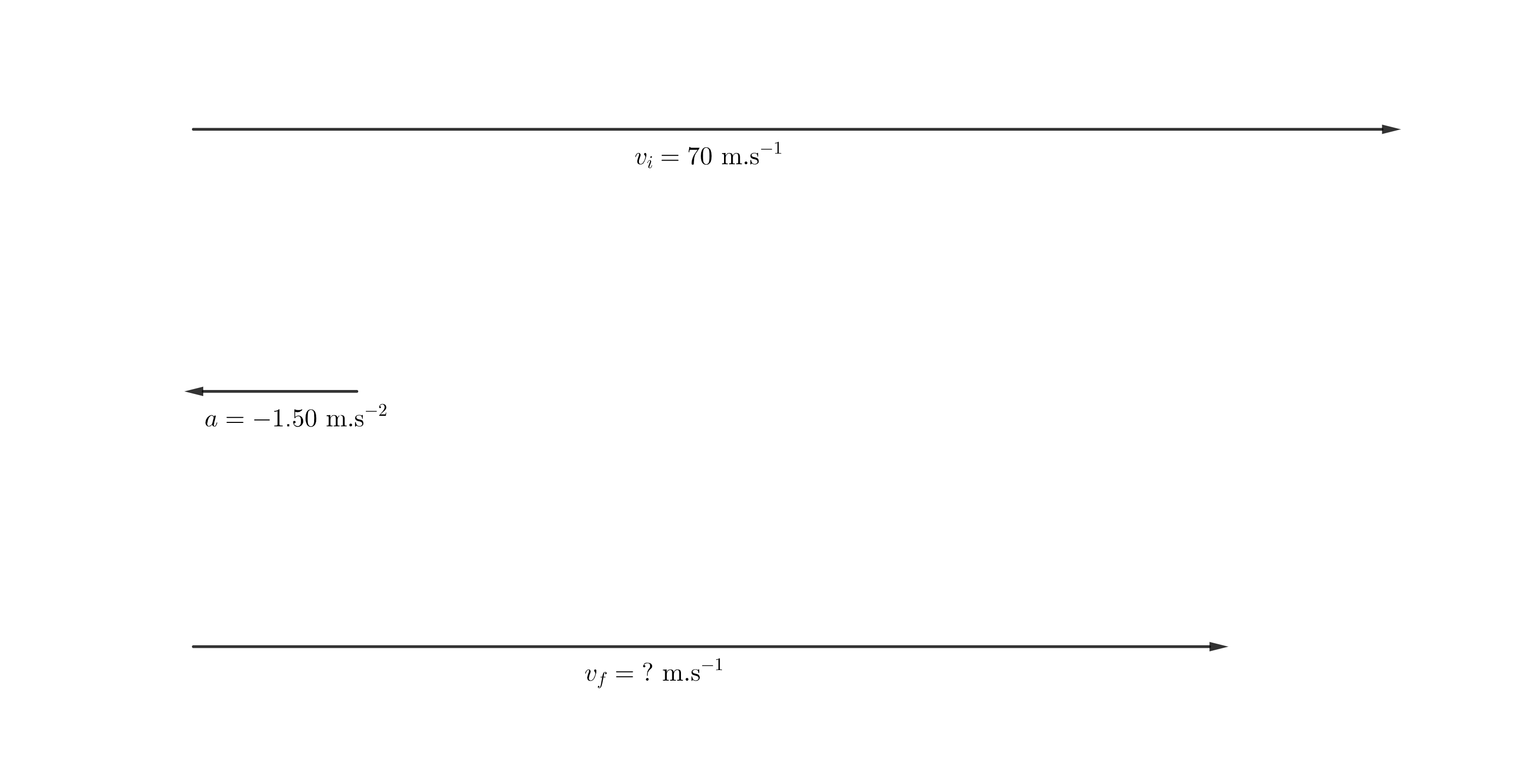
Note: A diagram like this is simply to help you make sense of the information that you have been given and that you need to find. You are not going to use it to do vector addition, therefore it does not need to be perfectly accurate.
In the diagram, we assign moving to the right as the positive direction. Therefore, the deceleration is acting in the opposite direction (i.e to the left), and is thus negative.
We have been given the following information:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=70\text{ m}\text{.}{{\text{s}}^{{-1}}}\\a&=-1.50\text{ m}\text{.}{{\text{s}}^{{-2}}} && \text{Remember this acts in the opposite direction }\\ &&&\text{to the velocity}\\\Delta t&=40.0\text{ s}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{v}_{f}}&={{v}_{i}}+a.\Delta t\quad \text{This equation relates what we know and what we want to find }({{v}_{f}})\\&=70\text{ m}\text{.}{{\text{s}}^{{-1}}}-1.50\text{ m}\text{.}{{\text{s}}^{{-2}}}\times 40.0\text{ s}\\&=\text{10 m}\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex]
The answer makes sense. After a period of deceleration, we expect the final velocity to be less than the initial velocity.
Example 1.2
Dragsters can achieve average accelerations of [latex]\scriptsize 26.0\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. Suppose such a dragster accelerates from rest at this rate for [latex]\scriptsize 5.56\text{ s}[/latex]. How far does it travel in this time?
Solution
We have been asked to calculate a displacement given the initial velocity of the dragster, its rate of acceleration and the time it accelerates.
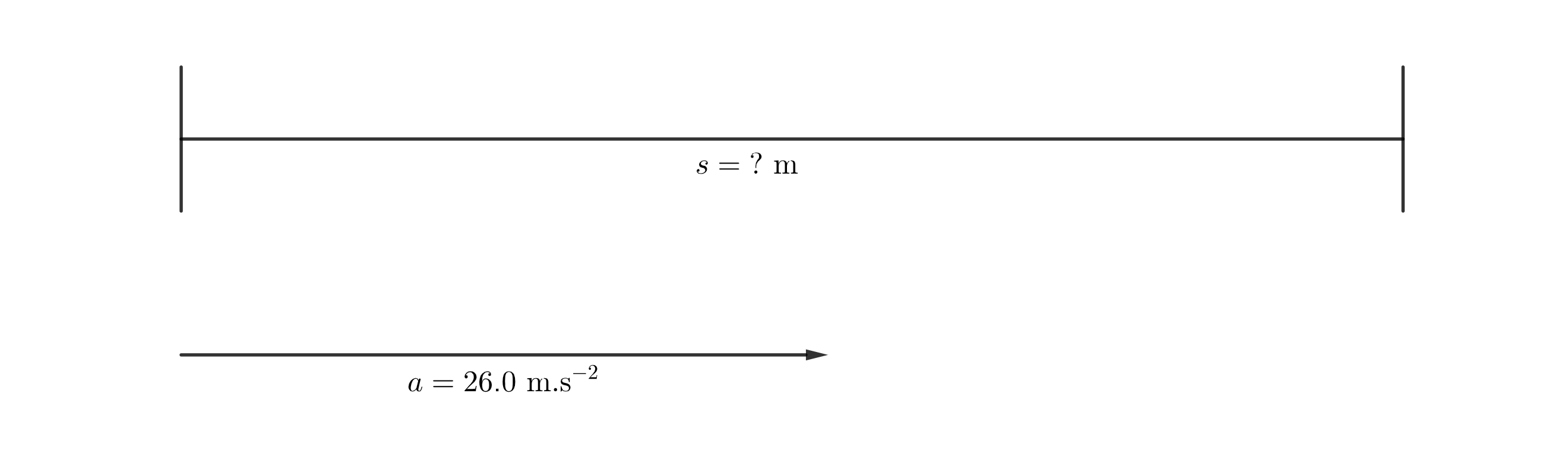
In the diagram, we assign moving to the right as the positive direction. Therefore, the acceleration is also acting in the same direction.
We have been given the following information:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=0\text{ m}\text{.}{{\text{s}}^{{-1}}}\\a&=26.0\text{ m}\text{.}{{\text{s}}^{{-2}}}\\\Delta t&=5.56\text{ s}\\\\s&={{v}_{i}}.\Delta t+\displaystyle \frac{1}{2}a.\Delta {{t}^{2}}\\&=\displaystyle \frac{1}{2}\times 26.0\text{ m}\text{.}{{\text{s}}^{{-2}}}\times {{(5.56\text{ s})}^{2}}\\&=401.88\text{ m}\end{align*}[/latex]
At just less than half a kilometre, the answer seems reasonable.
Example 1.3
A formula one (F1) racing car can accelerate from [latex]\scriptsize 0-100\text{ km/h}[/latex] in approximately [latex]\scriptsize 2.6\text{ s}[/latex]. If a car accelerates at this rate and covers [latex]\scriptsize 400\text{ m}[/latex], what will its final velocity be?
Solution
We have been asked to calculate the car’s final velocity. We have not been directly given the rate of acceleration. We will need to calculate what this is by using the fact that it can increase its velocity from [latex]\scriptsize {{v}_{i}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] to [latex]\scriptsize {{v}_{f}}=100\text{ km/h}[/latex] in [latex]\scriptsize 2.6\text{ s}[/latex].
Once we know the rate of acceleration, we can calculate the car’s final velocity if it accelerates at this rate over [latex]\scriptsize 400\text{ m}[/latex].
To calculate the acceleration, we have been given the following information:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=0\text{ m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}&=100\text{ km/h}=\displaystyle \frac{{100\text{ km/h}\times 1\ 000\text{ m}\text{.k}{{\text{m}}^{{-1}}}}}{{3\ 600\text{ s}\text{.}{{\text{h}}^{{-1}}}}}=27.78\text{ m}\text{.}{{\text{s}}^{{-1}}}\\\Delta t&=2.6\text{ s}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{\text{v}}_{f}} & ={{v}_{i}}+a.\Delta t\\\therefore a & =\displaystyle \frac{{({{v}_{f}}-{{v}_{i}})}}{{\Delta t}}\\ & =\displaystyle \frac{{27.78\text{ m}\text{.}{{\text{s}}^{{-1}}}}}{{2.6\text{ s}}}\\ & =10.68\text{ m}\text{.}{{\text{s}}^{{-2}}}\end{align*}[/latex]
Now we can calculate the final velocity, as we have the following information:
[latex]\scriptsize \begin{align*}s&=400\text{ m}\\a&=\text{10}\text{.68 m}\text{.}{{\text{s}}^{{-2}}}\\{{v}_{i}}&=0\text{ }\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}{{v}_{f}}^{2} & ={{v}_{i}}^{2}+2as\\ & =0\text{ }{{\text{m}}^{2}}\text{.}{{\text{s}}^{{-2}}}+2\times 10.68\text{ m}\text{.}{{\text{s}}^{{-2}}}\times 400\text{ m}\\ & =8\ 544\text{ }{{\text{m}}^{2}}.{{\text{s}}^{{-2}}}\\\therefore {{v}_{f}} &=92.43\text{ m}\text{.}{{\text{s}}^{{-1}}}\end{align*}[/latex]
[latex]\scriptsize 92.43\text{ m}\text{.}{{\text{s}}^{{-1}}}=\displaystyle \frac{{92.43\text{ m}\text{.}{{\text{s}}^{{-1}}}\times 3\ 600\text{ s}\text{.}{{\text{h}}^{{-1}}}}}{{1\ 000\text{ m}\text{.k}{{\text{m}}^{{-1}}}}}=332.76\text{ km/h}[/latex]. As the top speed of a F1 car is a little less than [latex]\scriptsize 360\text{ km/h}[/latex] this answer is reasonable.
Example 1.4
On a dry road surface, a car can decelerate at a rate of [latex]\scriptsize 6.92\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex], whereas on a wet surface it can decelerate at only [latex]\scriptsize 4.89\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex].
- Find the distances necessary to stop a car moving at [latex]\scriptsize 120\text{ km/h}[/latex] on:
- a dry road
- a wet road.
- Now, taking into account that the average driver takes about [latex]\scriptsize 0.500\text{ s}[/latex] between realising they need to brake and actually depressing the brake pedal, what should the actual following distances be in dry and wet conditions?
Solutions
- We have been asked to calculate the stopping distances. In each case the car is travelling at an initial velocity of [latex]\scriptsize 120\text{ km/h}[/latex] and needs to come to a stop. Therefore [latex]\scriptsize {{v}_{i}}=120\text{ km/h}[/latex] and [latex]\scriptsize {{v}_{f}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Also, we are considering deceleration, meaning that the rate of acceleration will be negative compared to the initial velocity.
.
We have been given the following information:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=120\text{ km/h}=33.33\text{ m}\text{.}{{\text{s}}^{{-1}}}\\{{v}_{f}}&=0\text{ m}\text{.}{{\text{s}}^{{-1}}}\\a&=-6.92\text{ m}\text{.}{{\text{s}}^{{-2}}}\ \text{(part a) and}\ a=-4.89\text{ m}\text{.}{{\text{s}}^{{-2}}}\ \text{(part b)}\end{align*}[/latex]

- .
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}^{2} & ={{v}_{i}}^{2}+2as\\\therefore s & =\displaystyle \frac{{({{v}_{f}}^{2}-{{v}_{i}}^{2})}}{{2a}}\\ & =\displaystyle \frac{{(0\text{ }{{\text{m}}^{2}}\text{.}{{\text{s}}^{{\text{-2}}}}-1\ 110.89\text{ }{{\text{m}}^{2}}\text{.}{{\text{s}}^{{-2}}})}}{{2\times (-6.92\text{ m}\text{.}{{\text{s}}^{{-2}}})}}\\ & =80.27\text{ m}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}^{2} & ={{v}_{i}}^{2}+2as\\\therefore s & =\displaystyle \frac{{({{v}_{f}}^{2}-{{v}_{i}}^{2})}}{{2a}}\\ & =\displaystyle \frac{{(0\text{ }{{\text{m}}^{2}}\text{.}{{\text{s}}^{{\text{-2}}}}-1\ 110.89\text{ }{{\text{m}}^{2}}\text{.}{{\text{s}}^{{-2}}})}}{{2\times (-4.89\text{ m}\text{.}{{\text{s}}^{{-2}}})}}\\ & =113.59\text{ m}\end{align*}[/latex]
.
It makes sense that the car will take longer to stop on a wet road where the deceleration is less than on a dry road.
- .
- We need to take account of the distance that the car will continue to travel before the brake pedal is depressed and, therefore, before the car starts to decelerate. Therefore, we need to add this distance to the distances calculated in question 1. Because there is no deceleration during this time, the same distance will be travelled on dry and wet roads.
.
We have been given the following information:
[latex]\scriptsize \begin{align*}v&=33.33\text{ m}\text{.}{{\text{s}}^{{-1}}}\\t&=0.500\text{ s}\\\\s&=v\times t\\&=33.33\text{ m}\text{.}{{\text{s}}^{{-1}}}\times 0.500\text{ s}\\&=16.67\text{ m}\end{align*}[/latex]
.
This means that the safe following distance on a dry road is at least [latex]\scriptsize 80.27\text{ m}+16.67\text{ m}=96.94\text{ m}[/latex] and at least [latex]\scriptsize \text{113}\text{.59 m}+16.67\text{ m}=130.26\text{ m}[/latex] on a wet road.
Example 1.5
A car merges into freeway traffic down a [latex]\scriptsize 200\text{ m}[/latex] ramp. If its initial velocity is [latex]\scriptsize 10\text{ m/s}[/latex]and it accelerates at [latex]\scriptsize 2.00\text{ m/}{{\text{s}}^{2}}[/latex], how long does it take to travel down the ramp?
Solution
We have been asked to calculate the time taken for the car to travel [latex]\scriptsize 200\text{ m}[/latex] at an initial velocity and an acceleration.
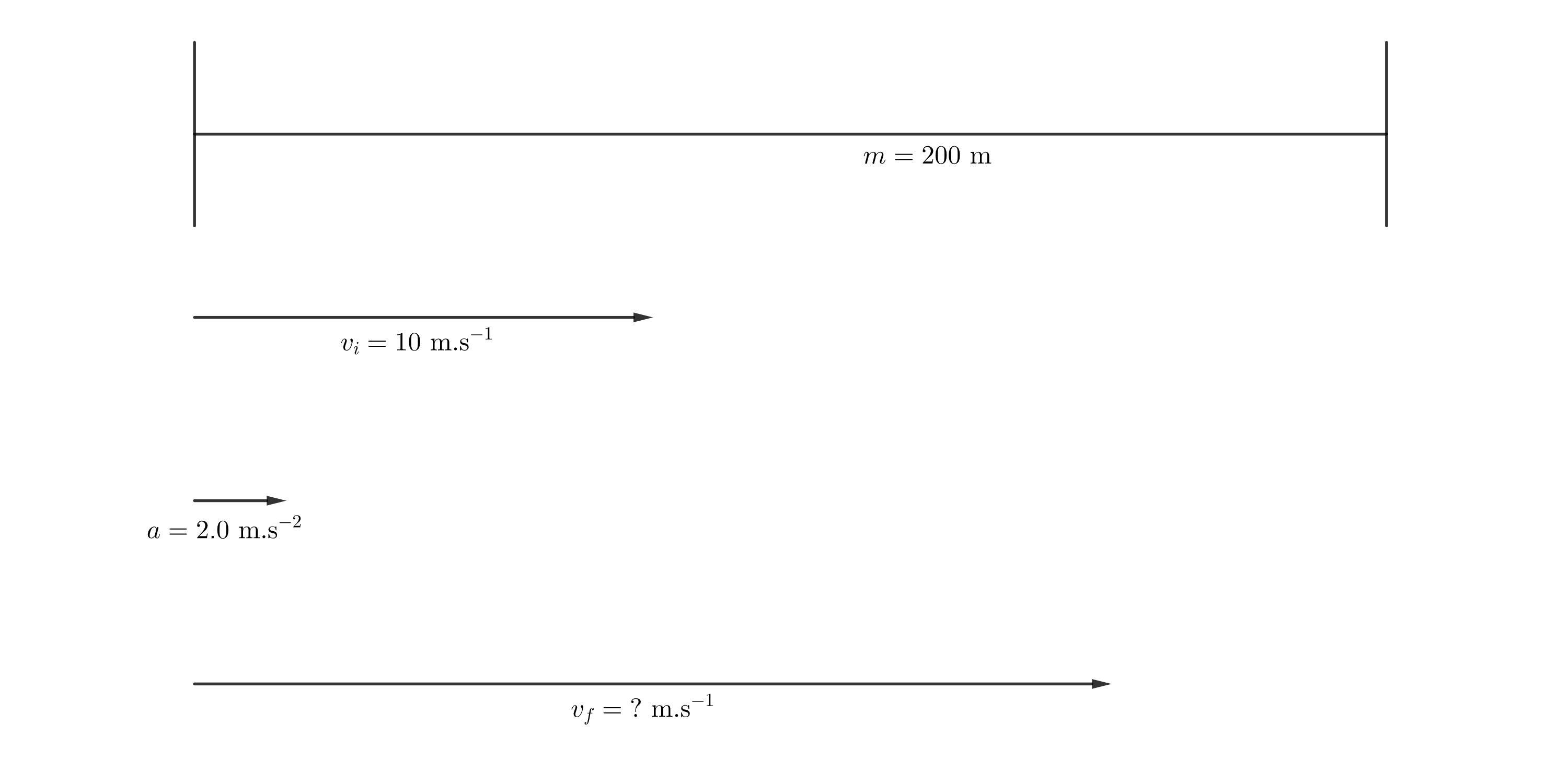
We have been given the following information:
[latex]\scriptsize \begin{align*}s&=200\text{ m}\\{{\text{v}}_{i}}&=10\text{ m}\text{.}{{\text{s}}^{{-1}}}\\a&=2\text{ m}{{\text{s}}^{{-2}}}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}s & ={{v}_{i}}.\Delta t+\displaystyle \frac{1}{2}a.\Delta {{t}^{2}}\\\therefore 200\text{ m} & =10\text{ m}\text{.}{{\text{s}}^{{-1}}}\times t+\displaystyle \frac{1}{2}\times 2\text{ m}\text{.}{{\text{s}}^{{-2}}}\times {{t}^{2}}\\\therefore 200 & =10t+{{t}^{2}}\quad \text{It helps to simplify the equation}\end{align*}[/latex]
This is a quadratic equation:
[latex]\scriptsize \begin{align*}{{t}^{2}}+10t-200 & =0\\\therefore (t-10)(t+20) & =0\\\therefore t=10\ \text{ o} & \text{r }t=-20\end{align*}[/latex]
An answer of [latex]\scriptsize t=-20\text{ s}[/latex] in this context does not make sense and we can discard it. Therefore, [latex]\scriptsize t=10\text{ s}[/latex].
Note: In some situations, both the answers we get from a quadratic equation may make sense, in which case we need to accept both of them.
Exercise 1.1
- A motorcycle has a uniform acceleration of [latex]\scriptsize 4\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex]. Assume the motorcycle has an initial velocity of [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Determine the velocity and displacement at the end of [latex]\scriptsize 12\text{ s}[/latex].
- An aeroplane accelerates uniformly such that it goes from rest to [latex]\scriptsize 144\text{ km/h}[/latex] in [latex]\scriptsize 8\text{ s}[/latex]. Calculate the acceleration required and the total distance that it has travelled in this time.
- A car is driven at [latex]\scriptsize 25\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex] in a municipal area. When the driver sees a traffic officer at a speed trap, he realises he is travelling too fast. He immediately applies the brakes of the car while still [latex]\scriptsize 100\text{ m}[/latex] away from the speed trap.
- Calculate the magnitude of the minimum acceleration which the car must have to avoid exceeding the speed limit if the municipal speed limit is [latex]\scriptsize 16.6\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- Calculate the time from the instant the driver applied the brakes until he reaches the speed trap. Assume that the car’s velocity, when reaching the trap, is [latex]\scriptsize 16.6\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- In towns and cities, the speed limit is [latex]\scriptsize 60\text{ km/h}[/latex]. The length of the average car is [latex]\scriptsize 3.5\text{ m}[/latex], and the width of the average car is [latex]\scriptsize 2\text{ m}[/latex]. To cross the road, you need to be able to walk further than the width of a car before that car reaches you. To cross safely, you should be able to walk at least [latex]\scriptsize 2\text{ m}[/latex] further than the width of the car ([latex]\scriptsize 4\text{ m}[/latex] in total) before the car reaches you.
- How long does it take you to walk a distance equal to the width of the average car?
- How many metres does a car travelling at the speed limit travel, in the same time that it takes you to walk a distance equal to the width of car?
- If you see a car driving toward you, and it is [latex]\scriptsize 28\text{ m}[/latex] away (the same as the length of eight cars), is it safe to walk across the road?
- How far away must a car be before you think it might be safe to cross? How many car-lengths is this distance?
The full solutions can be found at the end of the unit.
Summary
In this unit you have learnt the following:
- How to analyse and calculate more complex problems, using linear equations of motion:
- [latex]\scriptsize {{v}_{f}}={{v}_{i}}+a\Delta t[/latex]
- [latex]\scriptsize s={{v}_{i}}\Delta t+\displaystyle \frac{1}{2}a\Delta {{t}^{2}}[/latex]
- [latex]\scriptsize v_{f}^{2}=v_{i}^{2}+2as[/latex].
- A basic problem-solving strategy for solving problems of motion in one-dimension.
- That
- If an object ‘starts from rest’, then [latex]\scriptsize {{v}_{i}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- If an object ‘comes to rest’ OR stops, then [latex]\scriptsize {{v}_{f}}=0\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex].
- Slowing down means acceleration is negative while still moving in a positive direction.
- Constant velocity means [latex]\scriptsize \displaystyle a=0\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex], [latex]\scriptsize {{v}_{i}}={{v}_{f}}[/latex] and you can use [latex]\scriptsize \overset{\to }{\mathop{v}}\,\text{ = }\displaystyle \frac{{\Delta s}}{{\Delta t}}[/latex].
Unit 1: Assessment
Suggested time to complete: 40 minutes
- A ball is thrown and then caught in a padded mitt. If the deceleration of the ball is [latex]\scriptsize 2.10\times {{10}^{4}}\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex], and [latex]\scriptsize 1.85\text{ ms}[/latex] [latex]\scriptsize (1\text{ ms}={{10}^{{-3}}}\text{ s)}[/latex] elapses from the time the ball first touches the mitt until it stops, what was the initial velocity of the ball?
- A light-rail commuter train accelerates at a rate of [latex]\scriptsize 1.35\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex].
- How long does it take to reach its top speed of [latex]\scriptsize 80~\text{km/h}[/latex], starting from rest?
- The same train ordinarily decelerates at a rate of [latex]\scriptsize 1.65\ \text{m}\text{.}{{\text{s}}^{{-2}}}[/latex]. How long does it take to come to a stop from its top speed?
- In emergencies the train can decelerate more rapidly, coming to rest from [latex]\scriptsize 80~\text{km/h}[/latex], in [latex]\scriptsize 8.30\text{ s}[/latex]. What is its emergency deceleration in [latex]\scriptsize \text{m}\text{.}{{\text{s}}^{{-2}}}[/latex]?
- A bus on a straight road starts from rest at a bus stop and accelerates at [latex]\scriptsize 2\text{ m}\text{.}{{\text{s}}^{{-2}}}[/latex] until it reaches a speed of [latex]\scriptsize 20\text{ m}\text{.}{{\text{s}}^{{-1}}}[/latex]. Then the bus travels for [latex]\scriptsize 20\text{ s}[/latex] at a constant speed until the driver sees the next bus stop in the distance. The driver applies the brakes, stopping the bus in a uniform manner in [latex]\scriptsize 5~\text{s}[/latex],.
- How long does the bus take to travel from the first bus stop to the second bus stop?
- What is the average velocity of the bus during the trip?
- A world record was set for the men’s [latex]\scriptsize 100\text{ m}[/latex] dash in the 2008 Olympic Games in Beijing by Usain Bolt of Jamaica. Bolt ‘coasted’ across the finish line with a time of [latex]\scriptsize 9.69\text{ s}[/latex].
- If we assume that Bolt accelerated for [latex]\scriptsize 3.00\text{ s}[/latex] to reach his maximum speed and maintained that speed for the rest of the race, calculate his maximum speed and his acceleration.
- During the same Olympics, Bolt also set the world record in the [latex]\scriptsize 200\text{ m}[/latex] dash with a time of [latex]\scriptsize 19.30\text{ s}[/latex]. Using the same assumptions as for the [latex]\scriptsize 100\text{ m}[/latex] dash, what was his maximum speed for this race?
The full solutions can be found at the end of the unit.
Unit 1: Solutions
Exercise 1.1
- .
[latex]\scriptsize \begin{align*}{{v}_{i}}&=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=12\ \text{s}\\a&=4\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} & ={{v}_{i}}+at\\\therefore {{v}_{f}} & =20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}+4\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\times 12\ \text{s}=68\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}s&=vt+\displaystyle \frac{1}{2}a{{t}^{2}}\\&=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 12\ \text{s}+\displaystyle \frac{1}{2}\times 4\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\times {{(12\ \text{s})}^{2}}\\&=528\ \text{m}\end{align*}[/latex] - .
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{i}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=144\ \text{km/h}=\displaystyle \frac{{144\ \text{km/h}\times 1\ 000\ \text{m/km}}}{{3\ 600\ \text{s/hr}}}=40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=8\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}& ={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{t}=\displaystyle \frac{{40\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{8\ \text{s}}}=5\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}s&=vt+\displaystyle \frac{1}{2}a{{t}^{2}}\\&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 8\ \text{s}+\displaystyle \frac{1}{2}\times 5\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\times {{(8\ \text{s})}^{2}}\\&=160\ \text{m}\end{align*}[/latex] - .
- .
[latex]\scriptsize \begin{align*}{{v}_{i}}&=25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=16.6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\s&=100\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{v}_{f}}^{2} & ={{v}_{i}}^{2}+2as\\\therefore 2as & ={{v}_{f}}^{2}-{{v}_{i}}^{2}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}^{2}-{{v}_{i}}^{2}}}{{2s}}\\ & =\displaystyle \frac{{{{{\left( {16.6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}-{{{\left( {25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}}}{{2\times 100\ \text{m}}}\\ & =-1.75\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\end{align*}[/latex]
.
Therefore, the minimum acceleration is [latex]\scriptsize -1.75\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}[/latex] or a deceleration of [latex]\scriptsize 1.75\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}[/latex]. - .
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore t & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{a}=\displaystyle \frac{{16.6\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-25\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{-1.75\ \text{m}\text{.}{{\text{s}}^{{-2}}}}}=4.8\ \text{s}\end{align*}[/latex]
- .
- .
- .
[latex]\scriptsize \begin{align*}v&=5\ \text{km/h}=1.39\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\s&=4\ \text{m}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v & =\displaystyle \frac{s}{t}\\\therefore t & =\displaystyle \frac{s}{v}=\displaystyle \frac{{4\ \text{m}}}{{1.39\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}=2.88\ \text{s}\end{align*}[/latex] - We need to calculate the distance travelled by a car travelling at [latex]\scriptsize 60\ \text{km/h}[/latex] in [latex]\scriptsize 2.88\ \text{s}[/latex].
[latex]\scriptsize \begin{align*}v&=60\ \text{km/h}=16.67\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=2.88\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v &=\displaystyle \frac{s}{t}\\\therefore s & =v\times t=1.39\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 2.88\ \text{s}=48.01\ \text{m}\end{align*}[/latex] - No, it is not safe to cross. The time it takes the car to cover [latex]\scriptsize 28\ \text{m}[/latex] will be less than [latex]\scriptsize 2.88\ \text{s}[/latex] and, therefore, less than the time it will take a pedestrian to travel the [latex]\scriptsize 4\ \text{m}[/latex] considered safe when crossing a road.
- .
Unit 1: Assessment
- .
[latex]\scriptsize \begin{align*}{{v}_{f}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=1.85\times {{10}^{{-3}}}\ \text{s}\\a&=-2.10\times {{10}^{{-4}}}\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\quad \text{(deceleration is negative acceleration)}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore {{v}_{i}} & ={{v}_{f}}-at\\&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-\left( {-2.10\times {{{10}}^{{-4}}}\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}} \right)\times 1.85\times {{10}^{{-3}}}\ \text{s}\\&=38.85\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\end{align*}[/latex] - A light-rail commuter train accelerates at a rate of [latex]\scriptsize 1.35\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}[/latex].
- .
[latex]\scriptsize \begin{align*}{{v}_{i}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=80\ \text{km/h}=22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\a&=1.35\ \text{m}\text{.}{{\text{s}}^{{-2}}}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore t & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{a}=\displaystyle \frac{{22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{1.35\ \text{m}\text{.}{{\text{s}}^{{-2}}}}}=16.46\ \text{s}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{v}_{i}}&=22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\a&=-1.65\ \text{m}\text{.}{{\text{s}}^{{-2}}}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore t & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{a}=\displaystyle \frac{{0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{-1.65\ \text{m}\text{.}{{\text{s}}^{{-2}}}}}=13.47\ \text{s}\end{align*}[/latex] - .
[latex]\scriptsize \begin{align*}{{v}_{i}}&=22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=8.30\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{t}=\displaystyle \frac{{0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-22.22\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{8.30\ \text{s}}}=-2.68\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\end{align*}[/latex]
- .
- .
- Distance travelled during period of acceleration:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\a&=2\ \text{m}\text{.}{{\text{s}}^{{-2}}}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore t & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{a}=\displaystyle \frac{{20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{2\ \text{m}\text{.}{{\text{s}}^{{-2}}}}}=10\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}s&=vt+\displaystyle \frac{1}{2}a{{t}^{2}}\\&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 10\ \text{s}+\displaystyle \frac{1}{2}\times 2\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\times {{(10\ \text{s})}^{2}}\\&=100\ \text{m}\end{align*}[/latex]
.
Distance travelled during period of constant velocity:
[latex]\scriptsize \begin{align*}v&=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=20\ \text{s}\end{align*}[/latex]
[latex]\scriptsize \begin{align*}v&=\displaystyle \frac{s}{t}\\\therefore s & =v\times t=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 20\ \text{s}=400\ \text{m}\end{align*}[/latex]
.
Distance travelled during period of deceleration:
[latex]\scriptsize \begin{align*}{{v}_{i}}=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t=5\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}{{v}_{f}}&={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{t}=\displaystyle \frac{{0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}-20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{5\ \text{s}}}=-4\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}s&=vt+\displaystyle \frac{1}{2}a{{t}^{2}}\\&=20\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\times 5\ \text{s}+\displaystyle \frac{1}{2}\times \left( {-4\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}} \right)\times {{(5\ \text{s})}^{2}}\\&=50\ \text{m}\end{align*}[/latex]
Therefore, the total distance travelled by the bus is [latex]\scriptsize 100\ \text{m}+400\ \text{m}+50\ \text{m}=550\ \text{m}[/latex]. - [latex]\scriptsize \text{Average velocity}=\displaystyle \frac{{\text{Total displacement}}}{{\text{Total time}}}[/latex]
Total displacement: [latex]\scriptsize 550\ \text{m}[/latex]
Total time: [latex]\scriptsize 35\ \text{s}[/latex]
[latex]\scriptsize \text{Average velocity}=\displaystyle \frac{{550\ \text{m}}}{{35\ \text{s}}}=15.71\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]
- Distance travelled during period of acceleration:
- .
- Let Usain Bolt’s maximum speed be [latex]\scriptsize x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. He travelled at this maximum speed for [latex]\scriptsize 9.69\ \text{s}-3.00\ \text{s}=6.69\ \text{s}[/latex].
For the period of acceleration:
[latex]\scriptsize \begin{align*}{{v}_{i}}&=0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\{{v}_{f}}&=x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=3\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}{{v}_{f}}^{2} & ={{v}_{i}}^{2}+2as\\\therefore 2as &={{v}_{f}}^{2}-{{v}_{i}}^{2}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}^{2}-{{v}_{i}}^{2}}}{{2s}}\\ & =\displaystyle \frac{{{{{\left( {x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}-{{{\left( {0\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}} \right)}}^{2}}}}{{2s}}\\ & =\displaystyle \frac{{{{x}^{2}}}}{{2s}}\quad \text{Equation 1}\end{align*}[/latex]
.
[latex]\scriptsize \displaystyle \begin{align*}\text{But }{{v}_{f}} &={{v}_{i}}+at\\\therefore at & ={{v}_{f}}-{{v}_{i}}\\\therefore a & =\displaystyle \frac{{{{v}_{f}}-{{v}_{i}}}}{t}=\displaystyle \frac{x}{3}\quad \text{Equation 2}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}\text{Therefore }\displaystyle \frac{{{{x}^{2}}}}{{2s}} & =\displaystyle \frac{x}{3}\\\therefore 3{{x}^{2}} & =2sx\\\therefore 3{{x}^{2}}-2sx & =0\\\therefore x(3x-2s) & =0\\\therefore x=0\text{ } & \text{or }x=\displaystyle \frac{{2s}}{3}\end{align*}[/latex]
.
But [latex]\scriptsize x[/latex] cannot be zero. Therefore, [latex]\scriptsize x=\displaystyle \frac{{2s}}{3}[/latex].
Now the displacement during the period of acceleration is equal to [latex]\scriptsize 100\ \text{m}[/latex] (the length of the race) less his displacement during constant velocity.
.
For the period of constant velocity:
[latex]\scriptsize \begin{align*}v&=x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=6.69\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v &=\displaystyle \frac{s}{t}\\\therefore s & =v\times t=6.69x\end{align*}[/latex]
Therefore, his displacement during acceleration is [latex]\scriptsize 100-6.69x[/latex]. We can substitute this for [latex]\scriptsize s[/latex] in [latex]\scriptsize x=\displaystyle \frac{{2s}}{3}[/latex].
.
[latex]\scriptsize \begin{align*}\text{Therefore }x & =\displaystyle \frac{{2(100-6.69x)}}{3}\\\therefore 3x & =200-13.38x\\\therefore 3x+13.38x & =200\\\therefore 16.38x & =200\\\therefore x & =12.21\end{align*}[/latex]
Therefore, Usain Bolt’s maximum velocity was [latex]\scriptsize 12.21\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]and his average acceleration was [latex]\scriptsize \displaystyle \frac{{12.21\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}}}{{3\ \text{s}}}=4.07\ \text{m}\text{.}{{\text{s}}^{{\text{-2}}}}[/latex]. - If we let his maximum velocity be [latex]\scriptsize x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex] again, we know from part a. that [latex]\scriptsize x=\displaystyle \frac{{2s}}{3}[/latex]. But his total displacement is now [latex]\scriptsize 200\ \text{m}[/latex] and he ran at his maximum velocity for [latex]\scriptsize 16.30\ \text{s}[/latex].
.
Therefore, for the period of constant velocity:
[latex]\scriptsize \begin{align*}v&=x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}\\t&=16.30\ \text{s}\end{align*}[/latex]
.
[latex]\scriptsize \begin{align*}v &=\displaystyle \frac{s}{t}\\\therefore s & =v\times t=16.30x\end{align*}[/latex]
.
Therefore, his displacement during acceleration is [latex]\scriptsize 200-16.30x[/latex]. We can substitute this for [latex]\scriptsize s[/latex] in [latex]\scriptsize x=\displaystyle \frac{{2s}}{3}[/latex].
.
[latex]\scriptsize \begin{align*}\text{Therefore }x & =\displaystyle \frac{{2(200-16.30x)}}{3}\\\therefore 3x & =400-32.60x\\\therefore 35.60x & =400\\\therefore x & =11.24\end{align*}[/latex]
Therefore, Usain Bolt’s maximum velocity was [latex]\scriptsize 11.24\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex].
- Let Usain Bolt’s maximum speed be [latex]\scriptsize x\ \text{m}\text{.}{{\text{s}}^{{\text{-1}}}}[/latex]. He travelled at this maximum speed for [latex]\scriptsize 9.69\ \text{s}-3.00\ \text{s}=6.69\ \text{s}[/latex].
Media Attributions
- example1.1 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.2 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.4 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
- example1.5 © Geogebra is licensed under a CC BY-SA (Attribution ShareAlike) license
