Unit outcomes

By the end of this unit you will be able to:

• Analyse and solve problems in electrical circuits calculating: pd, emf, resistance in series and parallel networks.
• Describe the purpose of a Wheatstone bridge.

What you should know

Before you start this unit, make sure you can:

• Identify resistors in series and resistors in parallel, and calculate equivalent resistance for both. Refer to level 3 subject outcome 4.3 unit 2 if you need help with this.

Introduction

Parts of the text in this unit were sourced from Siyavula Physical Science Gr 11 Learner’s Book, Chapter 11, released under a CC-BY licence.

Now that you understand Ohm’s law and the relationship between current and voltage, you will learn to apply the concept in series and parallel circuits.

Working with Ohm’s law in circuits

You can use Ohm’s law ([latex]\scriptsize R=\displaystyle \frac{V}{I}[/latex]) to solve circuit problems.

Example 3.1

Calculate the current ([latex]\scriptsize I[/latex]) in this circuit.

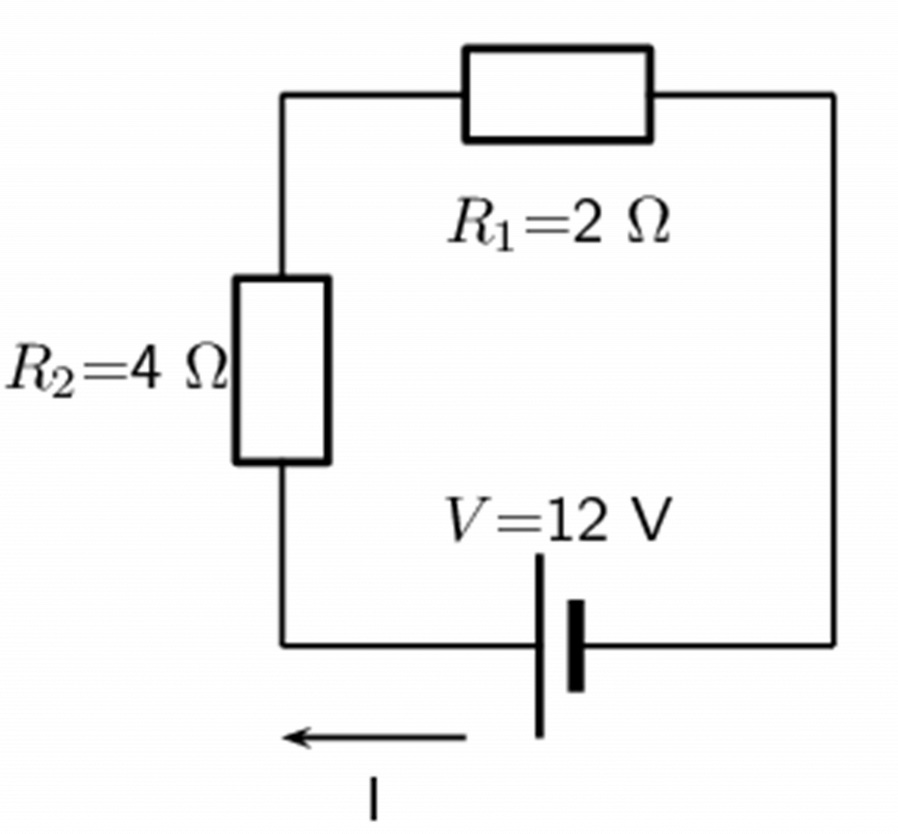
Solution

Step 1: Determine what is required

We are required to calculate the current flowing in the circuit.

Step 2: Determine how to approach the problem

We can use Ohm’s law. There are however two resistors in the circuit and we need to find the total resistance.

Step 3: Find the total resistance in circuit

Since the resistors are connected in series, the total (equivalent) resistance [latex]\scriptsize \text{R }[/latex]is:

[latex]\scriptsize {{R}_{s}}={{r}_{1}}+{{r}_{2}}[/latex]

Therefore:

[latex]\scriptsize \begin{align*}{{R}_{s}}&=2\text{ + 4 }\\&=\text{6 }\Omega \end{align*}[/latex]

Step 4: Apply Ohm’s law

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{12}}{6}\\&=2\text{ A}\end{align*}[/latex]

Step 5: Write the final answer

A current of [latex]\scriptsize 2\text{ A}[/latex] is flowing in the circuit.

Example 3.2

Two resistors are connected in series with a cell. Find the resistance of [latex]\scriptsize {{R}_{2}}[/latex], given that the current flowing through [latex]\scriptsize {{R}_{1}}[/latex] and [latex]\scriptsize {{R}_{2}}[/latex] is [latex]\scriptsize 0.25\text{ A}[/latex] and that the voltage across the cell is [latex]\scriptsize 1.5\text{ V}[/latex].

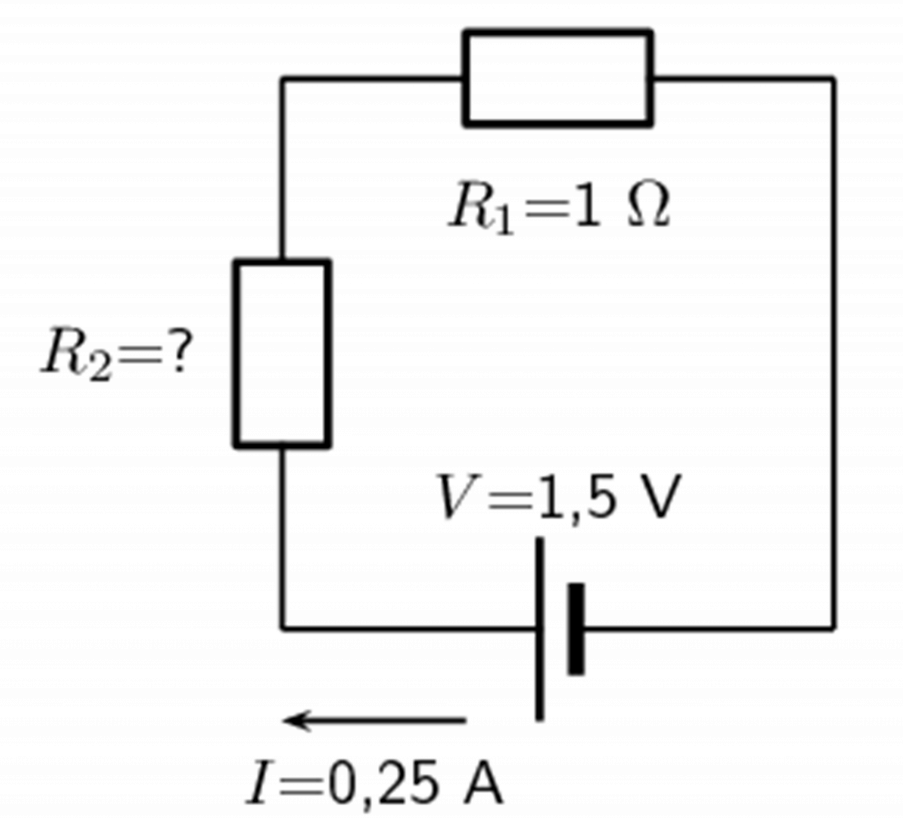
Solution

Step 1: Determine how to approach the problem

We can use Ohm’s law to find the total resistance [latex]\scriptsize R[/latex] in the circuit, and then calculate the unknown resistance using [latex]\scriptsize {{R}_{s}}={{r}_{1}}+{{r}_{2}}[/latex], because it is a series circuit.

Step 2: Find the total resistance

[latex]\scriptsize \begin{align*}R&=\displaystyle \frac{V}{I}\\&=\displaystyle \frac{{1.5}}{{0.25}}\\&=6\text{ }\Omega \end{align*}[/latex]

Step 3: Find the unknown resistance

We know that [latex]\scriptsize R=6\text{ }\Omega[/latex] and that [latex]\scriptsize {{R}_{1}}=1\text{ }\Omega[/latex].

Since [latex]\scriptsize {{R}_{s}}={{r}_{1}}+{{r}_{2}}[/latex], therefore:

[latex]\scriptsize \begin{align*}6&={{r}_{2}}+1\\{{r}_{2}}&=5\text{ }\Omega \end{align*}[/latex]

Step 4: Write the answer

[latex]\scriptsize {{R}_{2}}=5\text{ }\Omega[/latex]

Example 3.3

For the following circuit, calculate:

1. the voltage drops [latex]\scriptsize {{V}_{1}}[/latex], [latex]\scriptsize {{V}_{2}}[/latex] and [latex]\scriptsize {{V}_{3}}[/latex] across the resistors [latex]\scriptsize {{R}_{1}}[/latex], [latex]\scriptsize {{R}_{2}}[/latex] and [latex]\scriptsize {{R}_{3}}[/latex].
2. the resistance of [latex]\scriptsize {{R}_{3}}[/latex].
   

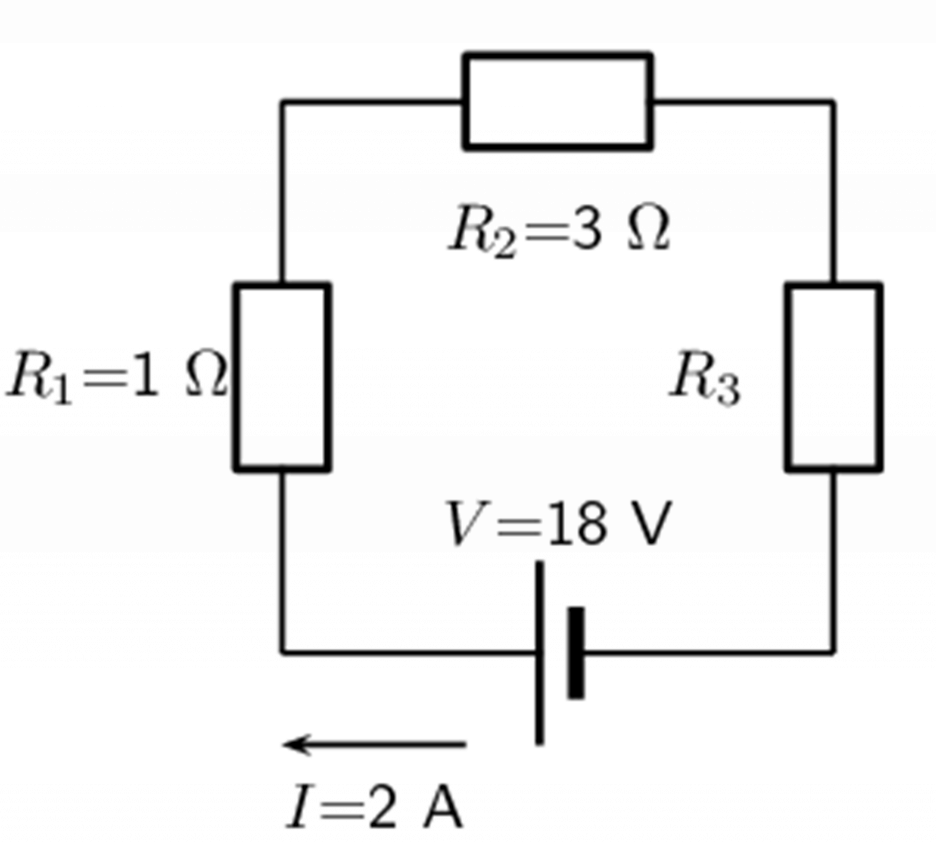
Solution

Step 1: Determine how to approach the problem

We are given the voltage across the cell and the current in the circuit, as well as the resistances of two of the three resistors. We can use Ohm’s law to calculate the voltage drop across the known resistors. Since the resistors are in a series circuit the voltage is [latex]\scriptsize {{V}_{{battery}}}={{V}_{1}}+{{V}_{2}}+{{V}_{3}}[/latex] and we can calculate [latex]\scriptsize {{V}_{3}}[/latex]. Then we can use this information to find the voltage across the unknown resistor [latex]\scriptsize {{R}_{3}}[/latex].

Step 2: Calculate voltage drop across [latex]\scriptsize {{R}_{1}}[/latex]

Using Ohm’s law:

[latex]\scriptsize \begin{align*}V&=IR\\&=2\text{ x 1 }\\&=\text{2 V}\end{align*}[/latex]

Step 3: Calculate voltage drop across [latex]\scriptsize {{R}_{2}}[/latex]

Again using Ohm’s law:

[latex]\scriptsize \begin{align*}V&=IR\\&=2\text{ x 3 }\\&=\text{6 V}\end{align*}[/latex]

Step 4: Calculate voltage drop across [latex]\scriptsize {{R}_{3}}[/latex]

Since the voltage drop across all the resistors combined must be the same as the voltage drop across the cell/battery in a series circuit, we can find [latex]\scriptsize {{V}_{3}}[/latex] using:

[latex]\scriptsize \begin{align*}{{V}_{{battery}}}&={{V}_{1}}+{{V}_{2}}+{{V}_{3}}\\18&=2+6+{{V}_{3}}\\\text{ }{{V}_{3}}&=10\text{ V}\end{align*}[/latex]

Step 5: Find the resistance of [latex]\scriptsize {{R}_{3}}[/latex]

We know the voltage across [latex]\scriptsize {{R}_{3}}[/latex] and the current through it, so we can use Ohm’s law to calculate the value for the resistance:

[latex]\scriptsize \begin{align*}R&=\displaystyle \frac{V}{I}\\&=\displaystyle \frac{{10}}{2}\\&=5\text{ }\Omega \end{align*}[/latex]

Step 6: Write the final answers

[latex]\scriptsize \begin{align*}{{V}_{1}}&=2\text{ V}\\{{V}_{2}}&=6\text{ V}\\{{V}_{3}}&=10\text{ V}\\{{R}_{1}}&=5\text{ }\Omega \end{align*}[/latex]

Example 3.4

Calculate the current ([latex]\scriptsize I[/latex]) in this circuit.

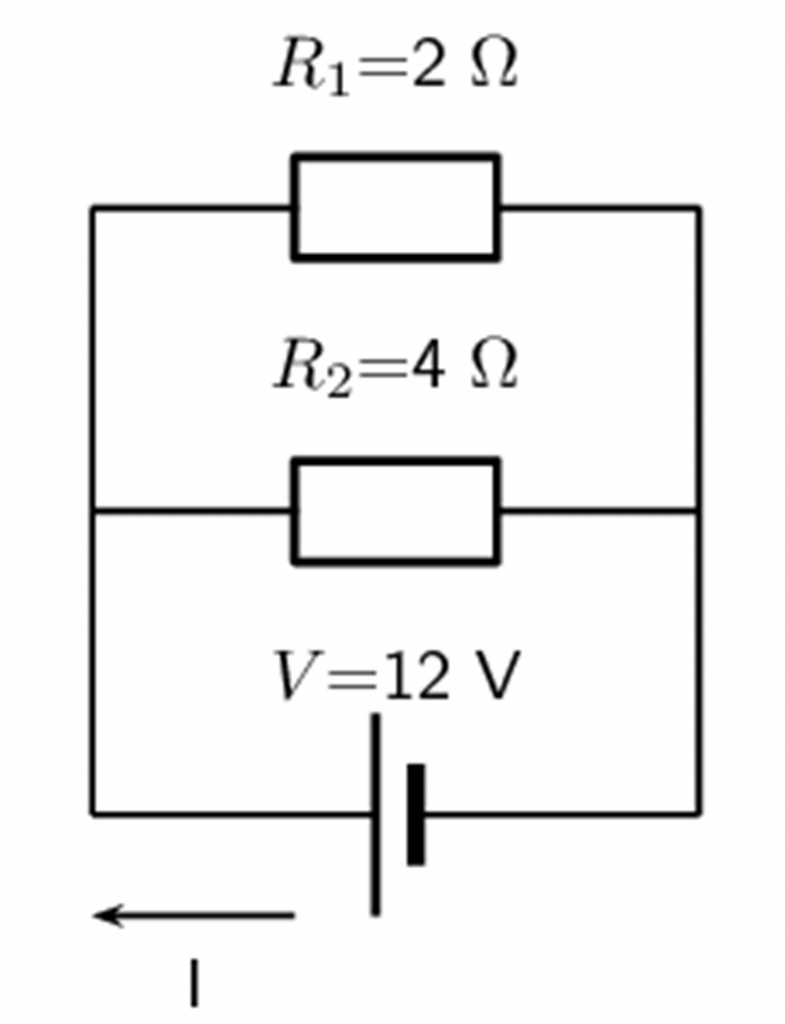
Solution

Step 1: Determine what is required

We are required to calculate the total current flowing in the circuit.

Step 2: Determine how to approach the problem

We can use Ohm’s law. There are however two resistors in the circuit and we need to find the total resistance.

Step 3: Find the total resistance in the circuit

Since the resistors are connected in parallel, the total (equivalent) resistance [latex]\scriptsize \text{R }[/latex]is:
[latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{2}+\displaystyle \frac{1}{4}\\\text{ }{{R}_{p}}&=1.33\text{ }\Omega \end{align*}[/latex]

Step 4: Apply Ohm’s law

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{12}}{{1.33}}\\&=\text{9 A}\end{align*}[/latex]

Step 5: Write the final answer

The current flowing in the circuit is [latex]\scriptsize 9\text{ A}[/latex].

Example 3.5

Two resistors ([latex]\scriptsize {{R}_{1}}[/latex] and [latex]\scriptsize {{R}_{2}}[/latex]) are connected in parallel with a cell. Find the resistance of [latex]\scriptsize {{R}_{2}}[/latex], given that the current flowing through the cell is [latex]\scriptsize 4.8\text{ A}[/latex] and that the voltage across the cell is [latex]\scriptsize 9\text{ V}[/latex].

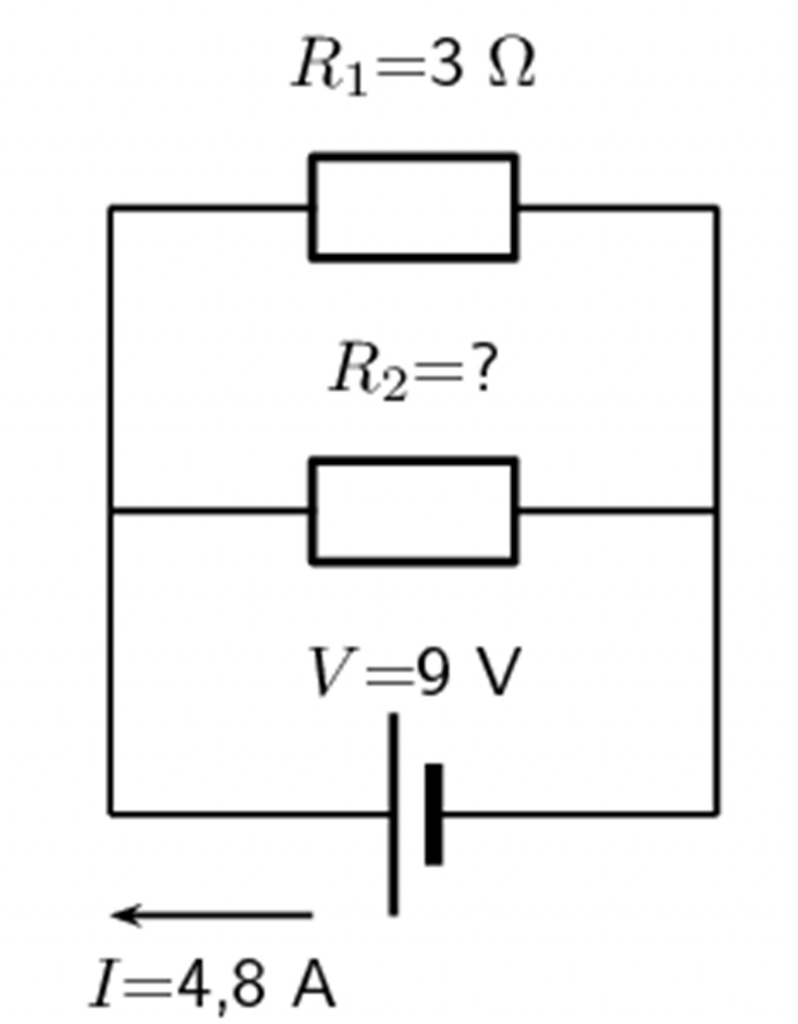
Solution

Step 1: Determine what is required

We need to calculate the resistance [latex]\scriptsize {{R}_{2}}[/latex].

Step 2: Determine how to approach the problem

Since we are given the voltage across the cell and the current through the cell, we can use Ohm’s law to find the equivalent resistance in the circuit.

[latex]\scriptsize \begin{align*}R&=\displaystyle \frac{V}{I}\\&=\displaystyle \frac{9}{{4.8}}\\&=\text{1}\text{.875 }\Omega \end{align*}[/latex]

Step 3: Calculate the value for [latex]\scriptsize {{R}_{2}}[/latex]

Since we know the equivalent resistance and the resistance of [latex]\scriptsize {{R}_{1}}[/latex], we can use the formula for resistors in parallel to find the resistance of [latex]\scriptsize {{R}_{2}}[/latex].

[latex]\scriptsize \begin{align*}\text{ }\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\\text{ }\displaystyle \frac{1}{{1.875}}&=\displaystyle \frac{1}{3}+\displaystyle \frac{1}{{{{r}_{2}}}}\\\text{ }{{r}_{2}}&=5\text{ }\Omega \end{align*}[/latex]

Step 4: Write the final answer

The resistance [latex]\scriptsize {{R}_{2}}[/latex] is [latex]\scriptsize 5\text{ }\Omega[/latex].

Example 3.6

An [latex]\scriptsize 18\text{ V}[/latex] cell is connected to two parallel resistors of [latex]\scriptsize 4\text{ }\Omega[/latex] and [latex]\scriptsize 12\text{ }\Omega[/latex]. Calculate the current through the cell and through each of the resistors.

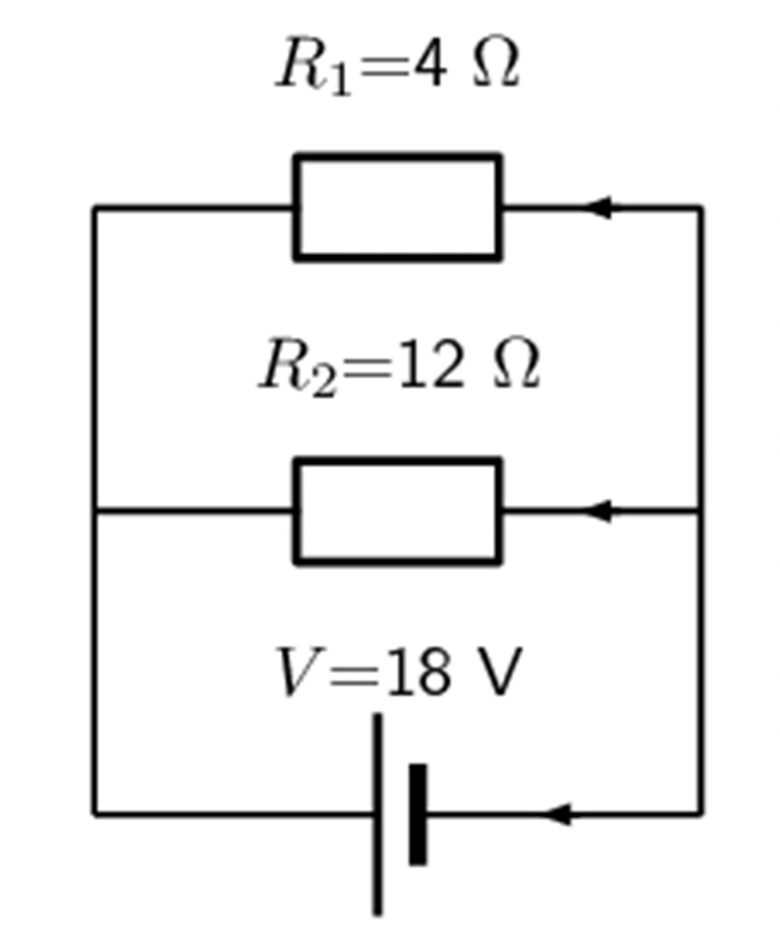
Solution

Step 1: Determine how to approach the problem

We need to determine the current through the cell and each of the parallel resistors. We have been given the potential difference across the cell and the resistances of the resistors, so we can use Ohm’s law to calculate the current.

Step 2: Calculate the current through the cell

To calculate the current through the cell we first need to determine the equivalent resistance of the rest of the circuit. The resistors are in parallel and therefore:

[latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{{12}}\\\text{ }{{R}_{p}}&=\text{ 3 }\Omega \end{align*}[/latex]

Now using Ohm’s law to find the current through the cell:

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{18}}{3}\\&=\text{6 A}\end{align*}[/latex]

Step 3: Now determine the current through one of the parallel resistors

We know that for a purely parallel circuit, the voltage across the cell is the same as the voltage across each of the parallel resistors. For this circuit:

[latex]\scriptsize V={{V}_{1}}={{V}_{2}}=18\text{ V}[/latex]

Let’s start with calculating the current through [latex]\scriptsize {{R}_{1}}[/latex] using Ohm’s law:

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{18}}{4}\\&=\text{4}\text{.5 A}\end{align*}[/latex]

Step 4: Calculate the current through the other parallel resistor

We can use Ohm’s law again to find the current in [latex]\scriptsize {{R}_{2}}[/latex]:

[latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{18}}{{12}}\\&=\text{1}\text{.5 A}\end{align*}[/latex]

An alternative method of calculating current through the [latex]\scriptsize 12\text{ }\Omega[/latex] resistor would have been to use the fact that the currents through each of the parallel resistors must add up to the total current through the cell:

[latex]\scriptsize \begin{align*}{{I}_{{total}}}&={{I}_{{4\Omega }}}+{{I}_{{12\Omega }}}\\\text{ 6}&= \text{4}\text{.5 + }{{\text{I}}_{{12\Omega }}}\\\text{ }{{I}_{{12\Omega }}}&=\text{1}\text{.5 A }\end{align*}[/latex]

Step 5: Write the final answers

The current through the cell is [latex]\scriptsize 6\text{ A}[/latex].

The current through the [latex]\scriptsize 4\text{ }\Omega[/latex]resistor is [latex]\scriptsize 4.5\text{ A}[/latex].

The current through the [latex]\scriptsize 12\text{ }\Omega[/latex] resistor is [latex]\scriptsize 1.5\text{ A}[/latex].

Exercise 3.1

1. Calculate the value of the unknown resistor in the circuit:
   
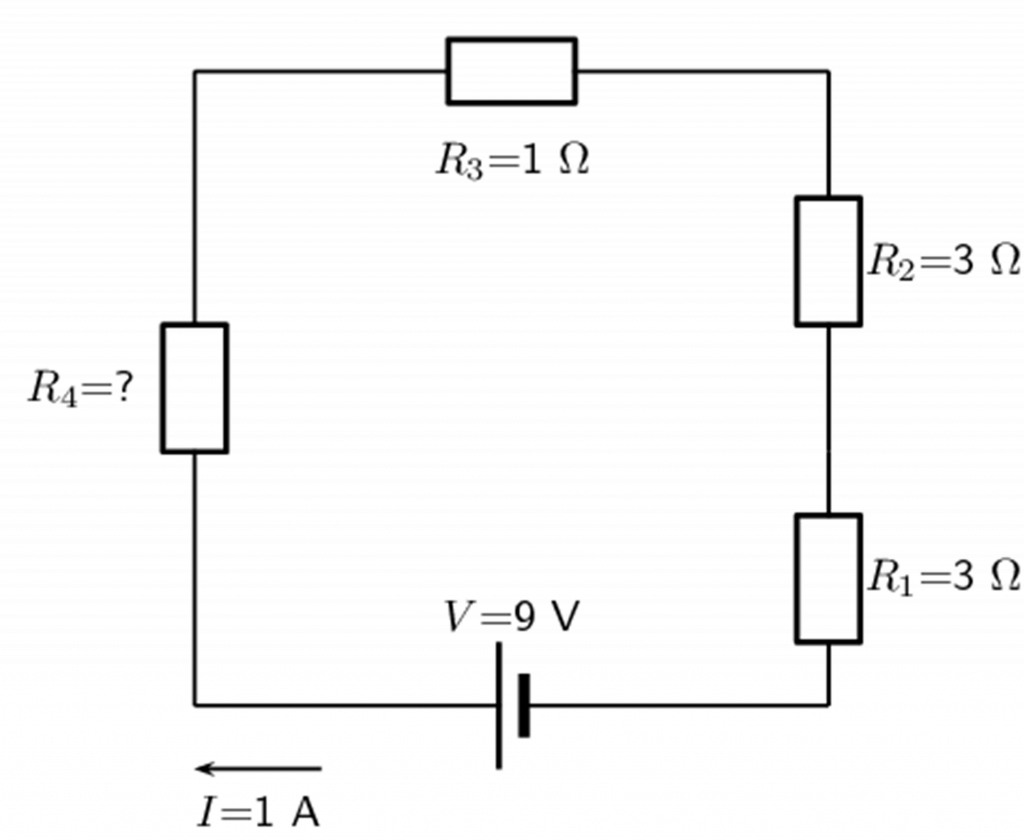
2. Calculate the value of the current in the following circuit:
   
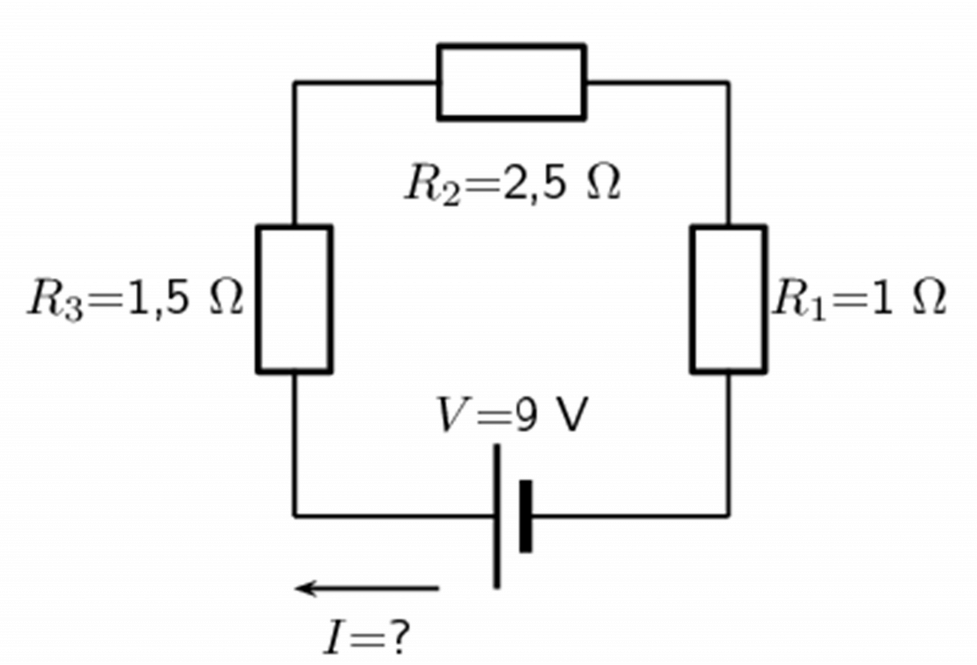
3. Three resistors with resistance [latex]\scriptsize 1\text{ }\Omega[/latex], [latex]\scriptsize 5\text{ }\Omega[/latex] and [latex]\scriptsize 10\text{ }\Omega[/latex] are connected in series with a [latex]\scriptsize 12\text{ V}[/latex] battery. Calculate the value of the current in the circuit.
   
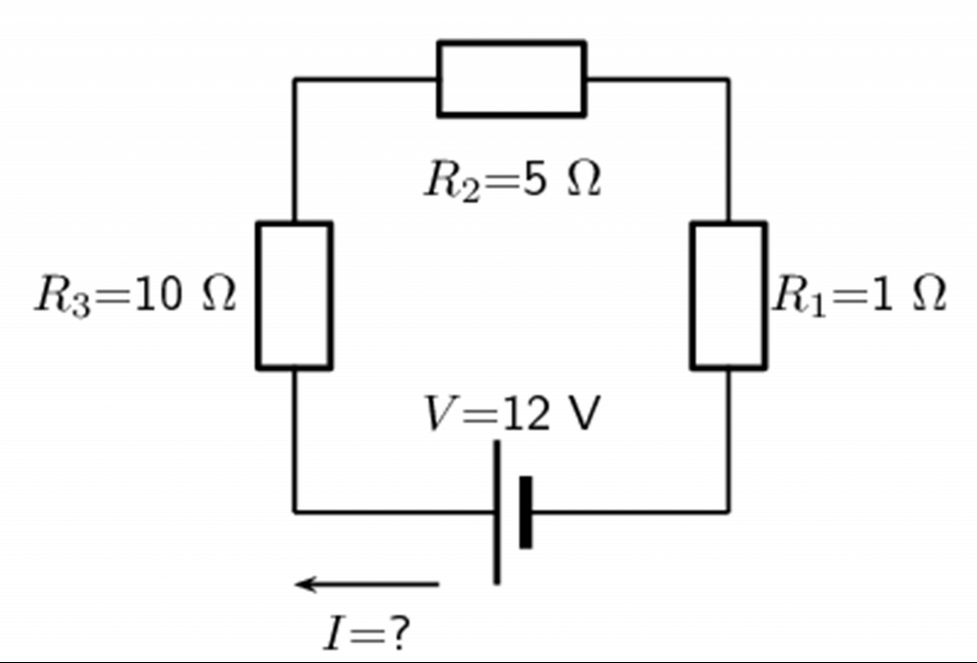
4. Calculate the current through the cell:
   
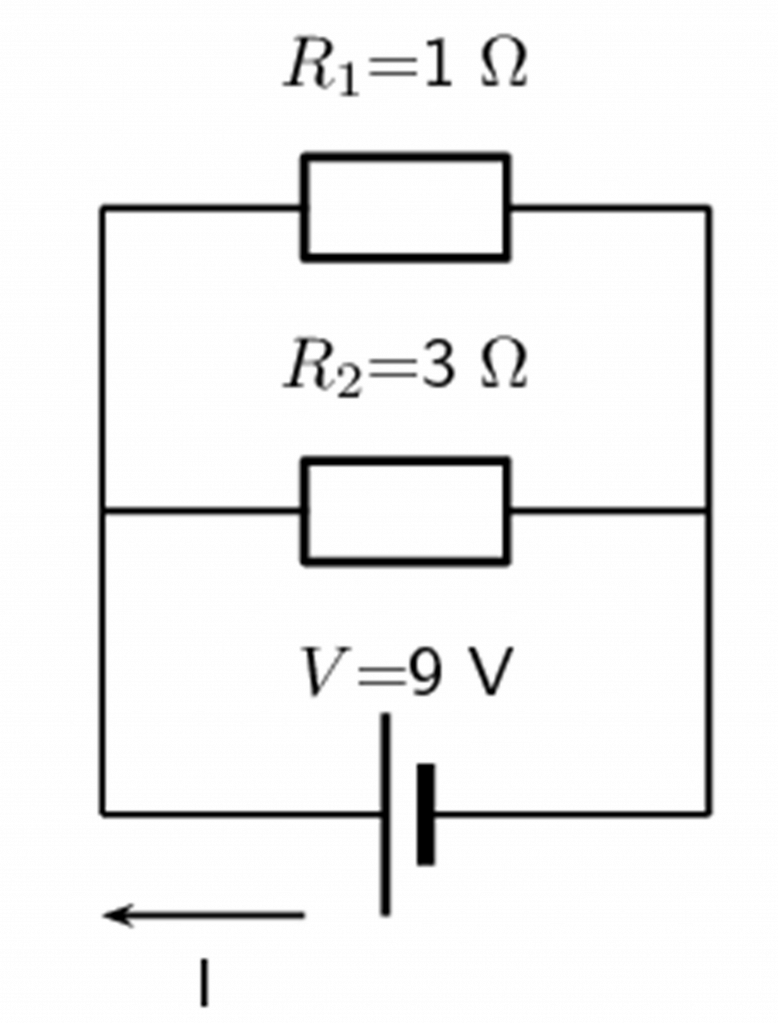
5. Calculate the value of the unknown resistor [latex]\scriptsize {{R}_{4}}[/latex] in the circuit:
   
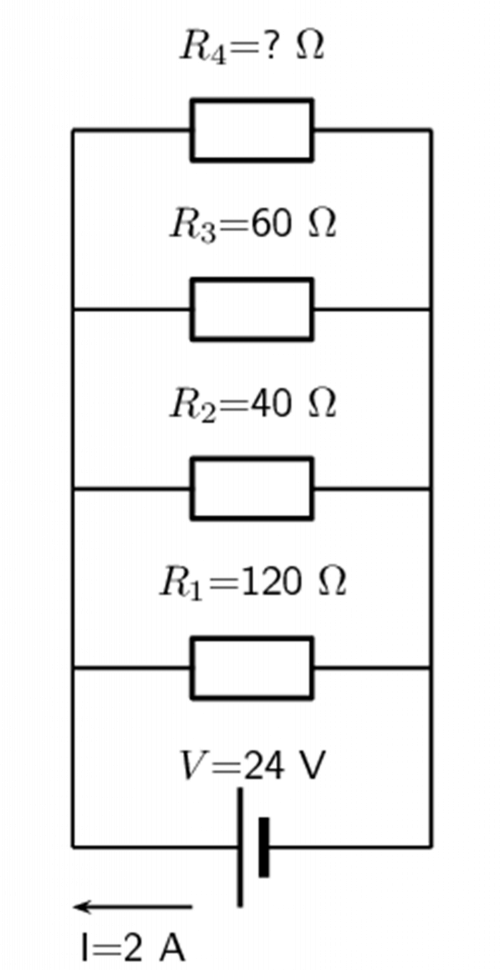
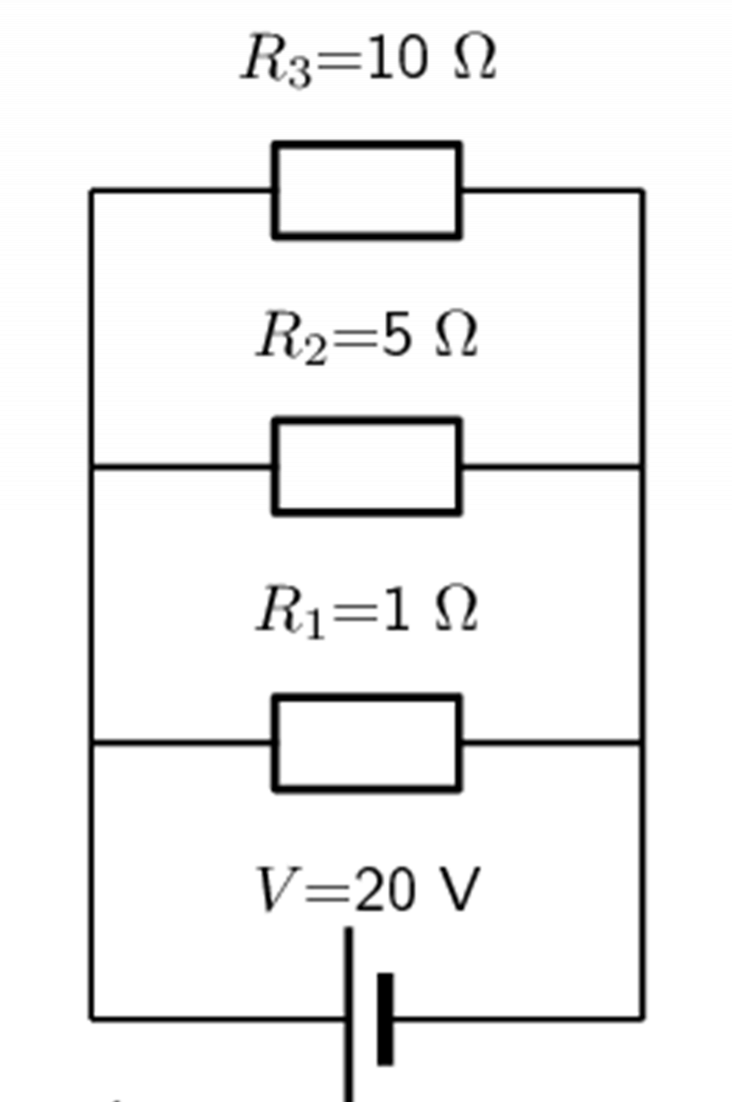
6. Three resistors with resistance [latex]\scriptsize 1\text{ }\Omega[/latex], [latex]\scriptsize 5\text{ }\Omega[/latex] and [latex]\scriptsize 10\text{ }\Omega[/latex] are connected in parallel with a [latex]\scriptsize 20\text{ V}[/latex] battery. Calculate the value of the total current in the circuit and through each individual resistor.
   

The full solutions are at the end of the unit.

Working with series and parallel resistors in one circuit

Now that you know how to handle simple series and parallel circuits, you are ready to tackle circuits which combine these two setups such as the following circuit:

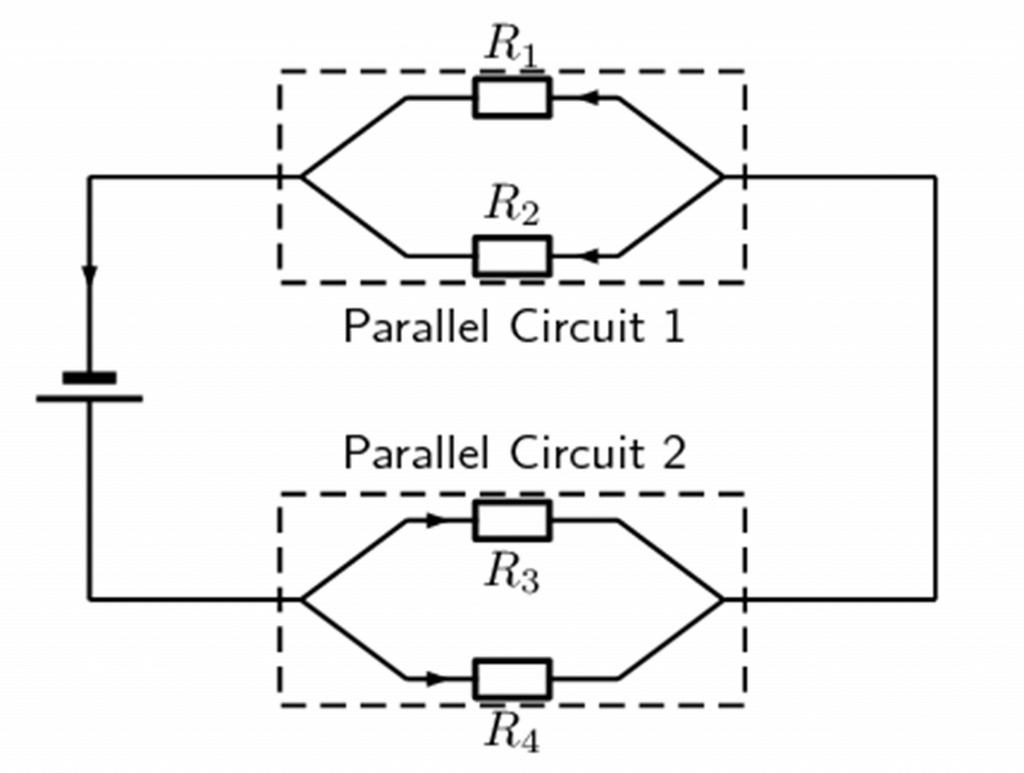
It is relatively easy to work out these kinds of circuits because you apply everything you have already learnt about series and parallel circuits. The only difference is that you do it in stages.

Example 3.7

Consider the circuit in figure 1. All the resistors have a resistance of [latex]\scriptsize 10\text{ }\Omega[/latex]. Calculate the equivalent resistance of the circuit.

Solution

The circuit consists of two parallel portions that are then in series with a cell. To work out the equivalent resistance for the circuit, you start by calculating the equivalent resistance of each of the parallel portions and then add up these resistances in series.

Step 1: Start by calculating the total resistance of Parallel Circuit 1

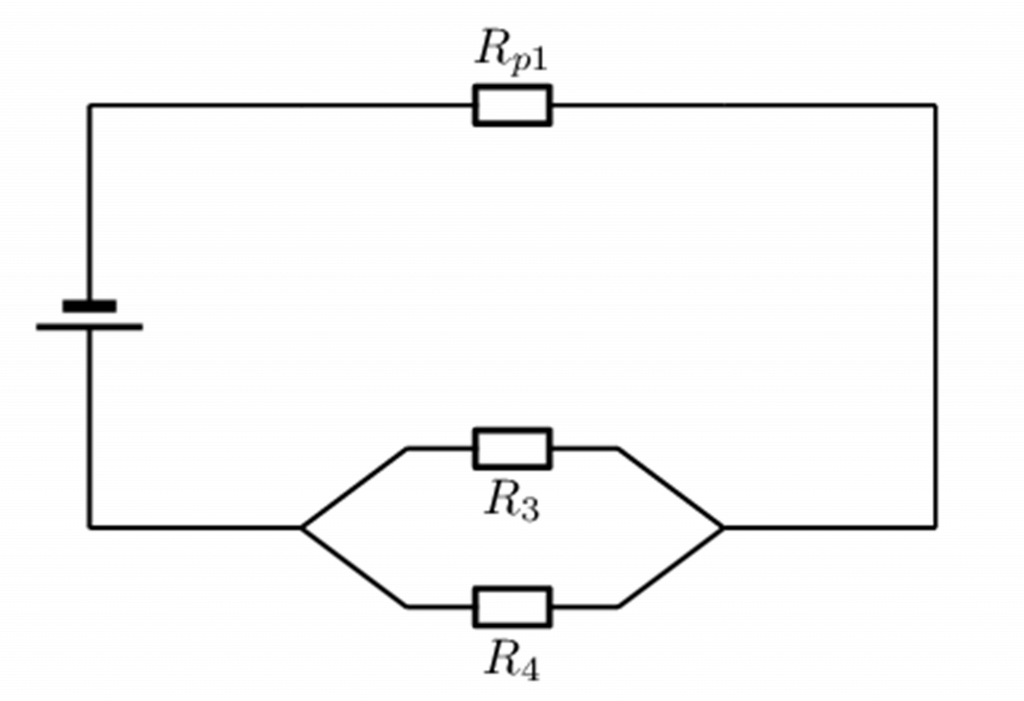
The value of [latex]\scriptsize {{R}_{{p1}}}[/latex] is:

[latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{{10}}+\displaystyle \frac{1}{{10}}\\\text{ }{{R}_{{p1}}}&=\text{ 5 }\Omega \end{align*}[/latex]

Step 2: Calculate the total resistance of Parallel Circuit 2 exactly as above

[latex]\scriptsize {{R}_{{p2}}}=5\text{ }\Omega[/latex]

Step 3: Now treat the circuit like a simple series circuit

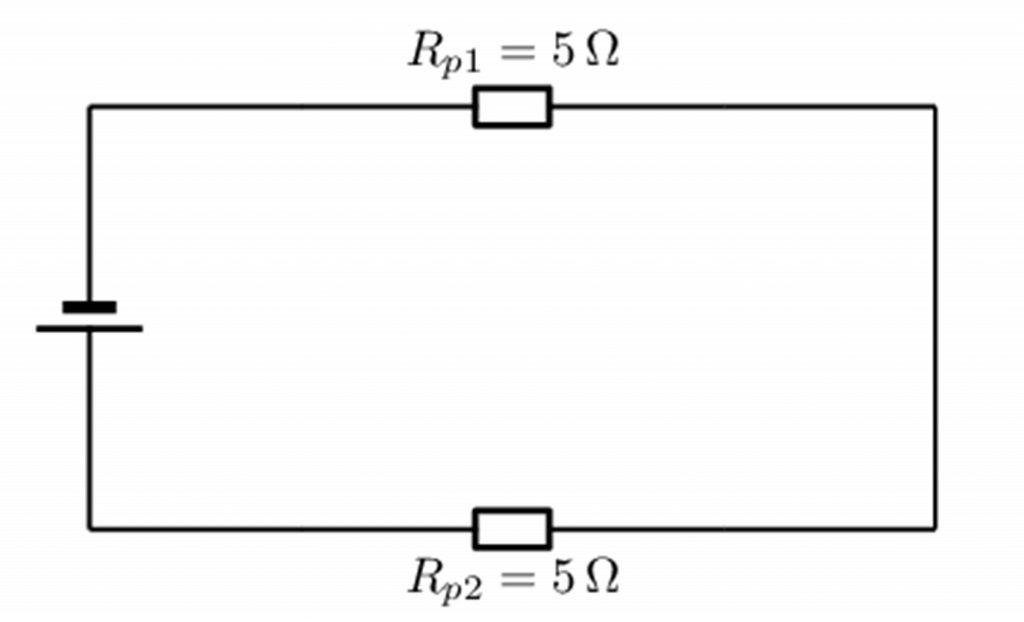
Therefore the equivalent resistance is:

[latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}\\&=\text{5 + 5}\\&=\text{10 }\Omega \end{align*}[/latex]

Exercise 3.2

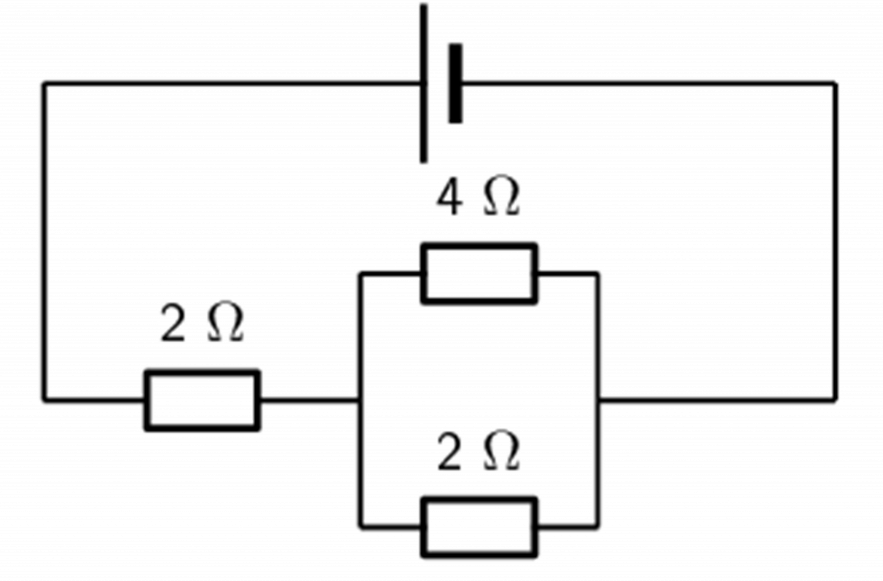
Determine the equivalent resistance of the following circuits:

1. .
   
2. .
   
3. .
   

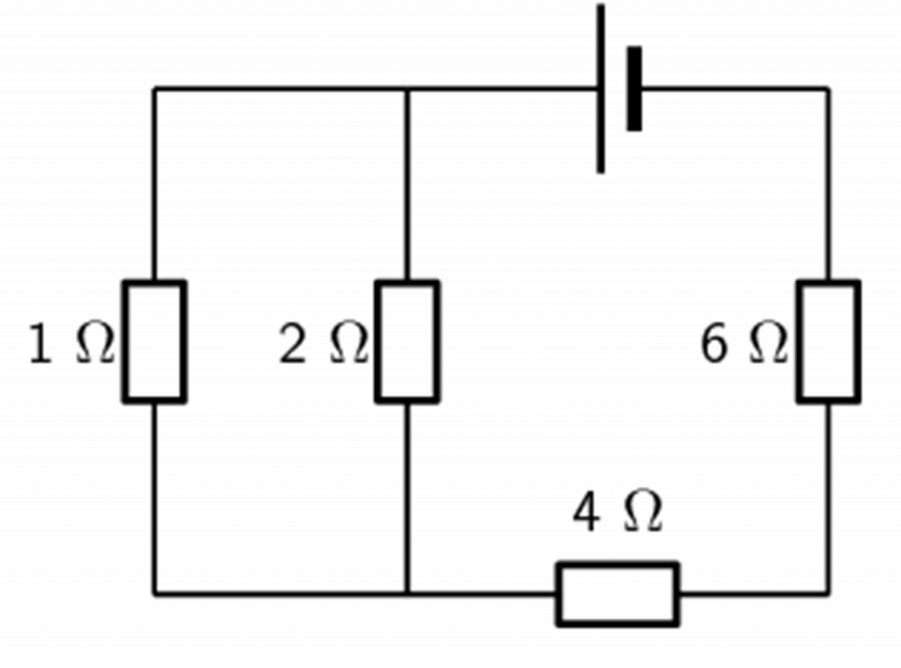
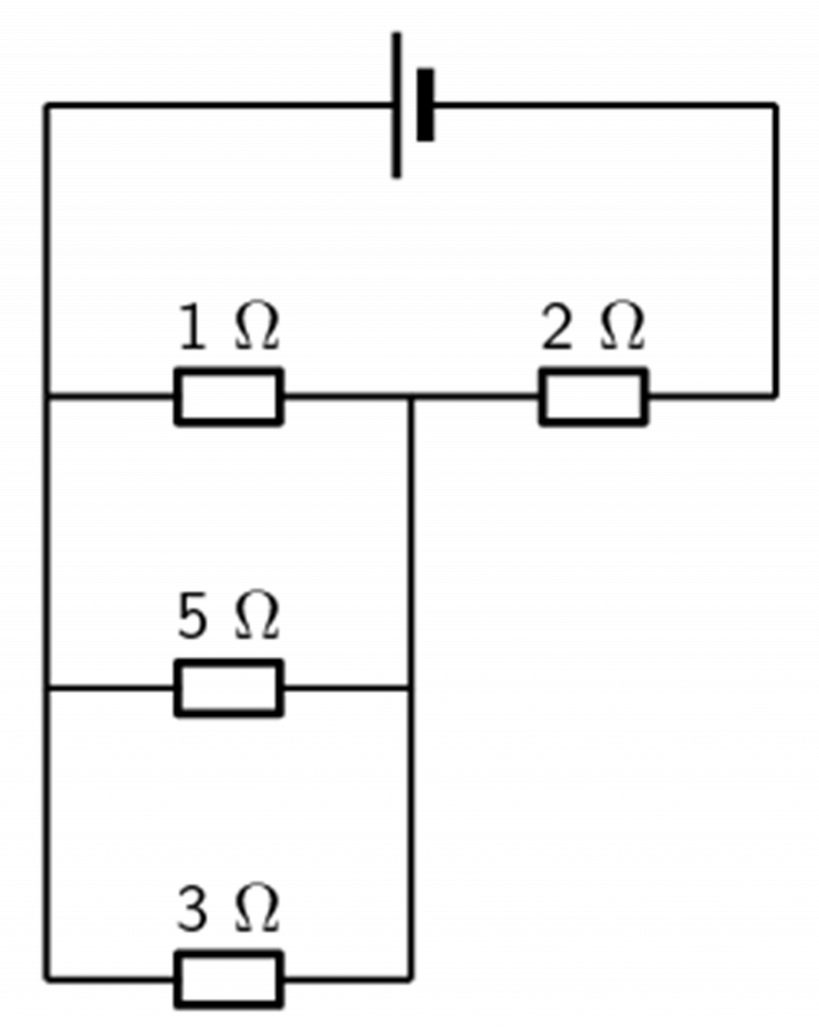
The full solutions are at the end of the unit.

The purpose of a Wheatstone bridge

The Wheatstone bridge was invented by Samuel Hunter Christie in 1833 and improved and popularised by Sir Charles Wheatstone in 1843.

A Wheatstone bridge is used to find the resistance of an unknown resistor. The Wheatstone bridge is the interconnection of four resistances forming a bridge. The four resistances in circuit are referred to as arms of the bridge. The bridge is used for finding the value of an unknown resistance connected with two known resistors, one variable resistor and a voltmeter or galvanometer. To find the value of unknown resistance, the resistance of the variable resistor is adjusted until the reading on the voltmeter or galvanometer is zero. This point is known as the balance point of the Wheatstone bridge.

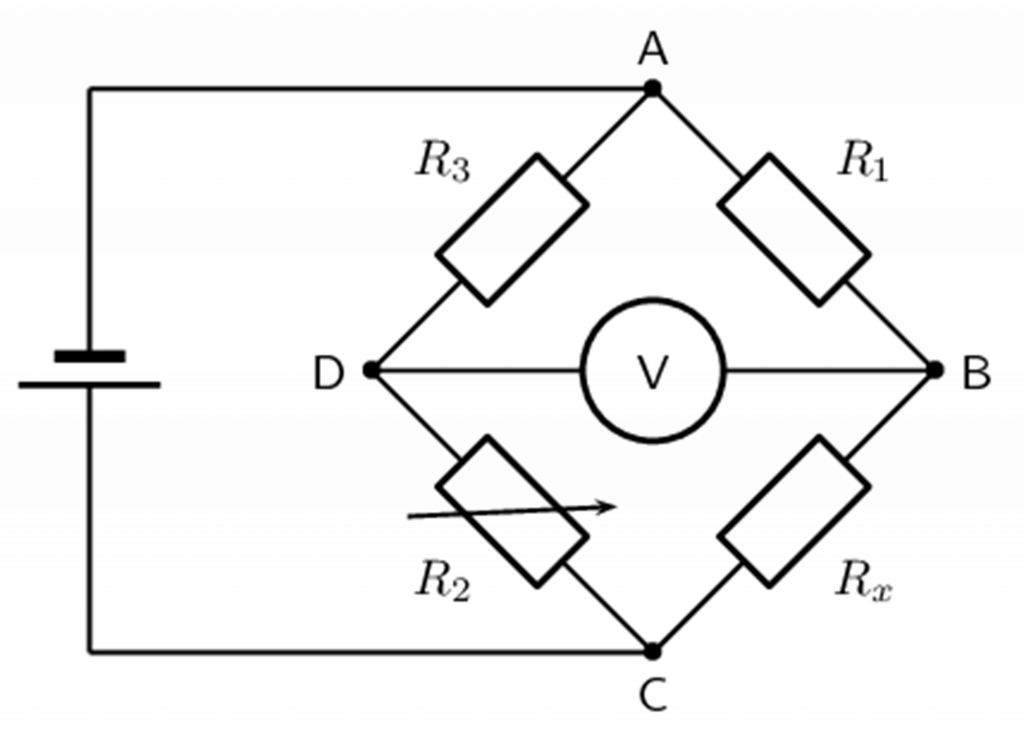
In the circuit of the Wheatstone bridge in figure 2, [latex]\scriptsize {{R}_{x}}[/latex] is the unknown resistance. [latex]\scriptsize {{R}_{1}}[/latex], [latex]\scriptsize {{R}_{2}}[/latex] and [latex]\scriptsize {{R}_{3}}[/latex] are resistors of known resistance and the resistance of [latex]\scriptsize {{R}_{2}}[/latex] is a rheostat (variable resistor). If the ratio of [latex]\scriptsize {{R}_{1}}:{{R}_{2}}[/latex] is equal to the ratio of [latex]\scriptsize {{R}_{x}}:{{R}_{3}}[/latex], then the potential difference between the two midpoints (D and B) will be zero and no current will flow between the midpoints. In order to determine the unknown resistance, [latex]\scriptsize {{R}_{2}}[/latex] is varied until this condition is reached. That is when the voltmeter reads [latex]\scriptsize 0\text{ V}[/latex]. The value of the unknown resistor can then be calculated using the formula:

[latex]\scriptsize {{R}_{x}}:{{R}_{3}}={{R}_{2}}:{{R}_{1}}[/latex]

Example 3.8

What is the resistance of the unknown resistor [latex]\scriptsize {{R}_{x}}[/latex] in the diagram below, if [latex]\scriptsize {{R}_{1}}=4\text{ }\Omega[/latex], [latex]\scriptsize {{R}_{2}}=8\text{ }\Omega[/latex] and [latex]\scriptsize {{R}_{3}}=6\text{ }\Omega[/latex].

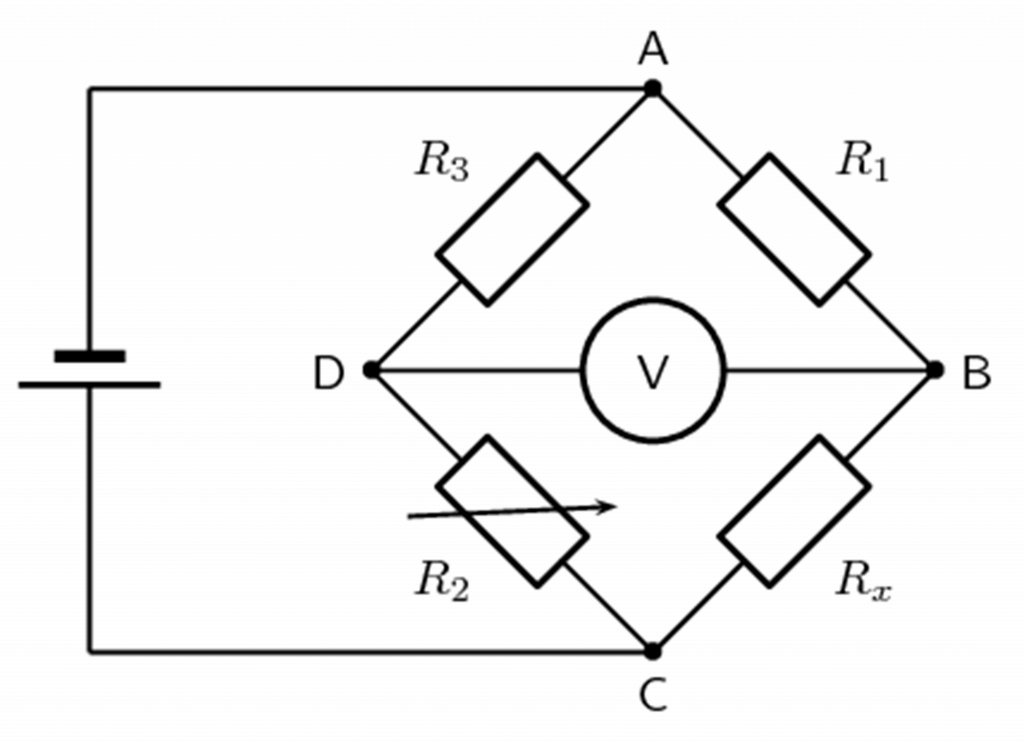
Solution

Step 1: Determine how to approach the problem

The arrangement is a Wheatstone bridge. So we use the equation:

[latex]\scriptsize {{R}_{x}}:{{R}_{3}}={{R}_{2}}:{{R}_{1}}[/latex]

Step 2: Substitute the values and solve the problem

[latex]\scriptsize \begin{align*}{{R}_{x}}:6&=8:4\\& or\\\displaystyle \frac{{{{R}_{x}}}}{6}&=\displaystyle \frac{8}{4}\\{{R}_{x}}&=12\text{ }\Omega \end{align*}[/latex]

Step 3: Write the final answer

The resistance of the unknown resistor is [latex]\scriptsize 12\text{ }\Omega[/latex].

Summary

• In circuits with series and parallel combinations of resistors, the equivalent resistance of the circuit must be worked out in stages.
• Ohm’s law ([latex]\scriptsize R=\displaystyle \frac{V}{I}[/latex]) can be applied to the whole circuit or different parts of a circuit.
• A Wheatstone bridge is an electrical device that can be used to find the resistance of an unknown resistor using the formula: [latex]\scriptsize {{R}_{x}}:{{R}_{3}}={{R}_{2}}:{{R}_{1}}[/latex].

Unit 3: Assessment

Suggested time to complete: 20 minutes

1. Examine the circuit below.
   
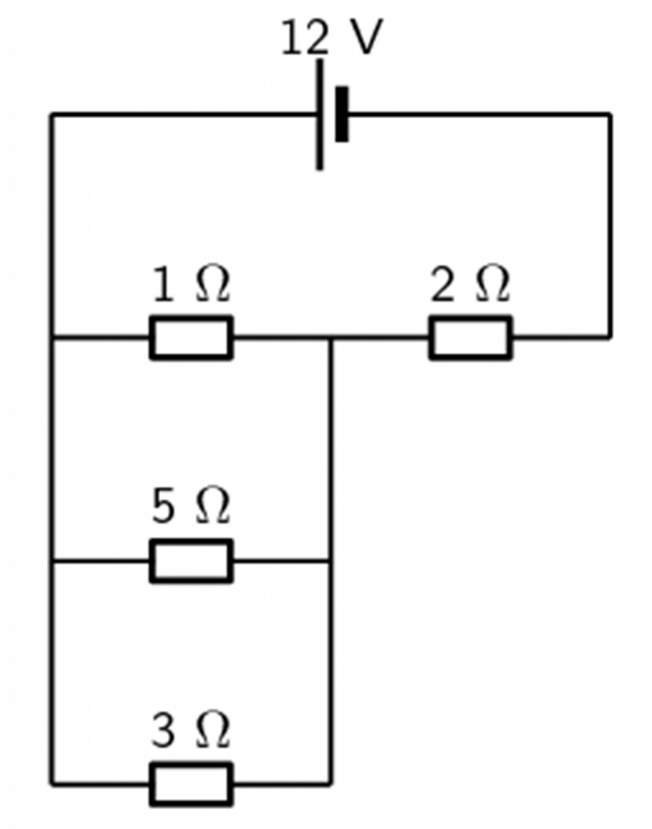
   If the potential difference across the cell is [latex]\scriptsize 12\text{ V}[/latex], calculate:
   1. the current [latex]\scriptsize I[/latex] through the cell.
   2. the current through the [latex]\scriptsize 5\text{ }\Omega[/latex] resistor.
2. Study the circuit diagram below. If the current flowing through the cell is [latex]\scriptsize 2\text{ A}[/latex], calculate the voltage across the cell and each of the resistors, [latex]\scriptsize {{R}_{1}}[/latex], [latex]\scriptsize {{R}_{2}}[/latex] and [latex]\scriptsize {{R}_{3}}[/latex].
   
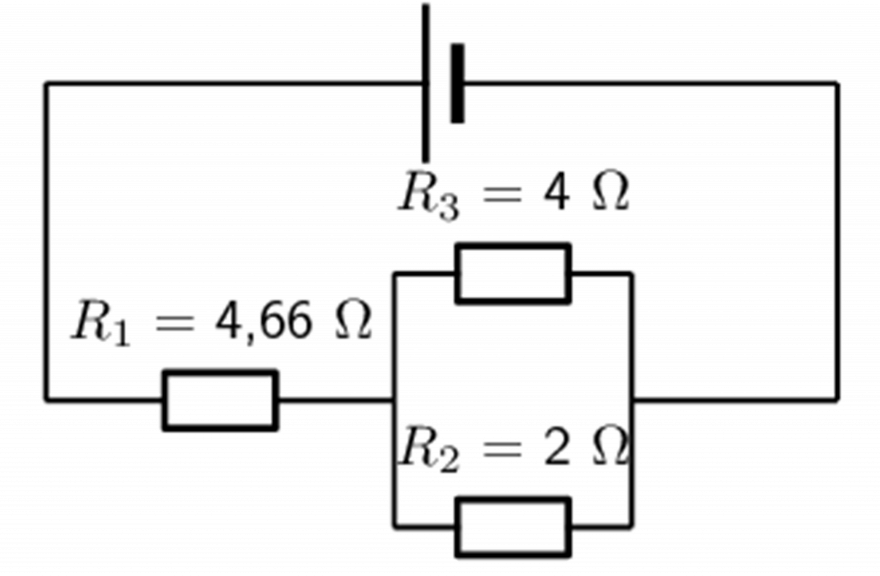
3. For the following circuit, calculate:
   
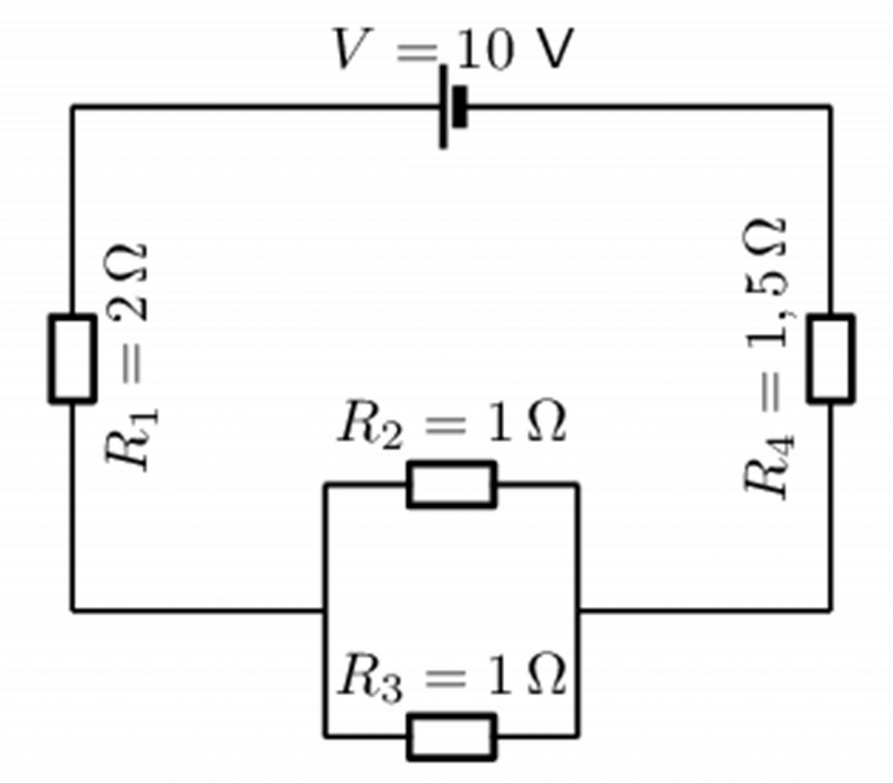
   1. the current through the cell
   2. the voltage drop across [latex]\scriptsize {{R}_{4}}[/latex]
   3. the current through [latex]\scriptsize {{R}_{2}}[/latex].
4. Describe how a Wheatstone bridge is used to find the resistance of an unknown resistor.
5. What is the resistance of the unknown resistor [latex]\scriptsize {{R}_{x}}[/latex] in the diagram below, if [latex]\scriptsize {{R}_{1}}=2\text{ }\Omega[/latex], [latex]\scriptsize {{R}_{2}}=4\text{ }\Omega[/latex] and [latex]\scriptsize {{R}_{3}}=9\text{ }\Omega[/latex].
   

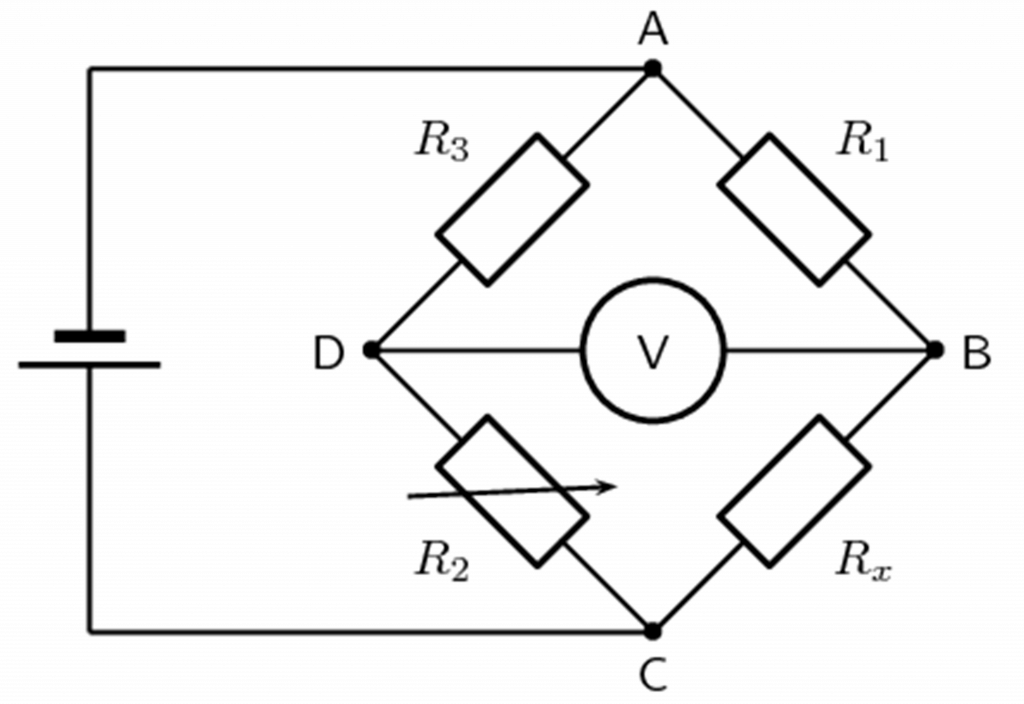
The full solutions are at the end of the unit.

Unit 3: Solutions

Exercise 3.1

1. We first use Ohm’s law to calculate the total series resistance:
   [latex]\scriptsize \begin{align*}R&=\displaystyle \frac{V}{I}\\&=\displaystyle \frac{9}{1}\\&=\text{9 }\Omega \end{align*}[/latex]
   Now find the unknown resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}+{{r}_{3}}+{{r}_{4}}\\\text{ 9}&= \text{3 + 3+1+}{{r}_{4}}\\\text{ }{{r}_{4}}&=\text{2 }\Omega \end{align*}[/latex]
2. First find the total resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}+{{r}_{3}}\\&=\text{1 + 2}\text{.5 + 1}\text{.5}\\&=\text{5 }\Omega \end{align*}[/latex]
   Now calculate the current:
   [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{9}{5}\\&=\text{1}\text{.8 A}\end{align*}[/latex]
3. Find the total resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}+{{r}_{3}}\\&=\text{1 + 5 + 10}\\&=\text{16 }\Omega \end{align*}[/latex]
   Now calculate the current:
   [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{12}}{{16}}\\&=\text{0}\text{.75 A}\end{align*}[/latex]
4. Find the total resistance:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{3}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.75 }\Omega \end{align*}[/latex]
   Now calculate the current:
   [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{9}{{0.75}}\\&=\text{12 A}\end{align*}[/latex]
5. Find the total resistance:
   [latex]\scriptsize \begin{align*}R&=\displaystyle \frac{V}{I}\\&=\displaystyle \frac{{24}}{2}\\&=\text{12 }\Omega \end{align*}[/latex]
   Now calculate the unknown resistance:
   [latex]\scriptsize \begin{align*}\text{ }\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}+\displaystyle \frac{1}{{{{r}_{3}}}}+\displaystyle \frac{1}{{{{r}_{4}}}}\\\text{ }\displaystyle \frac{1}{{12}}&=\displaystyle \frac{1}{{120}}+\displaystyle \frac{1}{{40}}+\displaystyle \frac{1}{{60}}+\displaystyle \frac{1}{{{{r}_{4}}}}\\\text{ }{{r}_{4}}&=30\text{ }\Omega \end{align*}[/latex]
6. To calculate the value of the current through the battery you first need to calculate the equivalent resistance:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}+\displaystyle \frac{1}{{{{r}_{3}}}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{5}+\displaystyle \frac{1}{{10}}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.77 }\Omega \end{align*}[/latex]
   Now calculate the current through the battery:
   [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{20}}{{0.77}}\\&=\text{26 A}\end{align*}[/latex]
   Now calculate the value of the current in each of the three resistors.
   For a parallel circuit the voltage across cell is the same as the voltage across each of the resistors. For this circuit:
   [latex]\scriptsize V={{V}_{1}}={{V}_{2}}={{V}_{3}}=20\text{ V}[/latex]
   Now use Ohm’s law for each resistor:
   [latex]\scriptsize \begin{align*}{{R}_{1}}:\text{ }I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{20}}{1}\\&=\text{20 A}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{R}_{2}}:\text{ }I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{20}}{5}\\&=\text{4 A}\end{align*}[/latex]
   [latex]\scriptsize \begin{align*}{{R}_{3}}:\text{ }I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{20}}{{10}}\\&=\text{2 A}\end{align*}[/latex]
   You can check that these add up to the total current ([latex]\scriptsize 20+4+2=26\text{ A}[/latex]).

Back to Exercise 3.1

Exercise 3.2

1. Start by determining the equivalent resistance of the parallel combination:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}\\\text{ }{{R}_{p}}&=\text{ 1}\text{.33 }\Omega \end{align*}[/latex]
   Now that you have a circuit with two resistors in series, you can calculate the equivalent resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}\\&=\text{2 + 1}\text{.33}\\&=\text{3}\text{.33 }\Omega \end{align*}[/latex]
2. Start by determining the equivalent resistance of the parallel combination:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{2}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.67 }\Omega \end{align*}[/latex]
   Now that you have a circuit with three resistors in series, you can calculate the equivalent resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}+{{r}_{3}}\\&=\text{4 + 6 + 0}\text{.67}\\&=\text{10}\text{.67 }\Omega \end{align*}[/latex]
3. Start by determining the equivalent resistance of the parallel combination:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}+\displaystyle \frac{1}{{r3}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{5}+\displaystyle \frac{1}{3}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.652 }\Omega \end{align*}[/latex]
   Now that you have a circuit with two resistors in series, you can calculate the equivalent resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}\\&=\text{2 + 0}\text{.652}\\&=\text{2}\text{.652 }\Omega \end{align*}[/latex]

Back to Exercise 3.2

Unit 3: Assessment

1. .
   1. Start by determining the equivalent resistance of the parallel combination:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}+\displaystyle \frac{1}{{{{r}_{3}}}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{5}+\displaystyle \frac{1}{3}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.652 }\Omega \end{align*}[/latex]
      Now that you have a circuit with two resistors in series, you can calculate the equivalent resistance:
      [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{2}}\\&=\text{2 + 0}\text{.652}\\&=\text{2}\text{.652 }\Omega \end{align*}[/latex]
      So the current through the cell is:
      [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{12}}{{2.652}}\\&=\text{4}\text{.52 A}\end{align*}[/latex]
   2. The current through the parallel combination of resistors is [latex]\scriptsize 4.52\text{ A}[/latex]. (The current is the same through series combinations of resistors and we can consider the entire parallel set of resistors as one series resistor.)
      Using this we can find the voltage through the parallel combination of resistors (remember to use the equivalent parallel resistance and not the equivalent resistance of the circuit):
      [latex]\scriptsize \begin{align*}V&=\displaystyle \frac{I}{R}\\&=\displaystyle \frac{{4.52}}{{0.652}}\\&=\text{2}\text{.95 V}\end{align*}[/latex]
      Since the voltage across each resistor in the parallel combination is the same, this is also the voltage across the [latex]\scriptsize 5\text{ }\Omega[/latex] resistor.
      So now you can calculate the current through the resistor:
      [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{2.95}}{5}\\&=\text{0}\text{.59 A}\end{align*}[/latex]
2. To find the voltage, first find the equivalent resistance. You start by calculating the equivalent resistance of the parallel combination:
   [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}\\\text{ }{{R}_{p}}&=\text{ 1}\text{.33 }\Omega \end{align*}[/latex]
   Now that you have a circuit with two resistors in series, you can calculate the equivalent resistance:
   [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{p}}\\&=\text{4}\text{.66 + 1}\text{.33}\\&=\text{5}\text{.99 }\Omega \end{align*}[/latex]
   So the voltage across the cell is:
   [latex]\scriptsize \begin{align*}V&=IR\\&=\text{2 x 5}\text{.99}\\&=\text{12 V}\end{align*}[/latex]
   The current through the parallel combination of resistors is [latex]\scriptsize 2\text{ A}[/latex]. (The current is the same through series combinations of resistors and you can consider the entire parallel set of resistors as one series resistor.)
   Using this, find the voltage through the each of the resistors. Start by finding the voltage across [latex]\scriptsize {{R}_{1}}[/latex]:
   [latex]\scriptsize \begin{align*}V&=IR\\&=\text{2 x 4}\text{.66}\\&=\text{9}\text{.32 V}\end{align*}[/latex]
   Now find the voltage across the parallel combination:
   [latex]\scriptsize \begin{align*}V&=IR\\&=\text{2 x 1}\text{.33}\\&=\text{2}\text{.66 V}\end{align*}[/latex]
   Since the voltage across each resistor in the parallel combination is the same, this is also the voltage across resistors [latex]\scriptsize {{R}_{2}}[/latex] and [latex]\scriptsize {{R}_{3}}[/latex].
3. .
   1. To find the current, first find the equivalent resistance. Start by calculating the equivalent resistance of the parallel combination:
      [latex]\scriptsize \begin{align*}\displaystyle \frac{1}{{{{R}_{p}}}}&=\displaystyle \frac{1}{{{{r}_{1}}}}+\displaystyle \frac{1}{{{{r}_{2}}}}\\&=\displaystyle \frac{1}{1}+\displaystyle \frac{1}{1}\\\text{ }{{R}_{p}}&=\text{ 0}\text{.5 }\Omega \end{align*}[/latex]
      Now that you have a circuit with two resistors in series, you can calculate the equivalent resistance:
      [latex]\scriptsize \begin{align*}{{R}_{s}}&={{r}_{1}}+{{r}_{4}}+{{r}_{p}}\\&=\text{2 + 1}\text{.5 + 0}\text{.5}\\&=\text{4 }\Omega \end{align*}[/latex]
      So the current through the cell is:
      [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{10}}{4}\\&=\text{2}\text{.5 A}\end{align*}[/latex]
   2. The current through all the resistors is [latex]\scriptsize 2.5\text{ A}[/latex]. (The current is the same through series combinations of resistors and we can consider the entire parallel set of resistors as one series resistor.)
      Using this, find the voltage through [latex]\scriptsize {{R}_{4}}[/latex]:
      [latex]\scriptsize \begin{align*}V&=IR\\&=\text{2}\text{.5 x 1}\text{.5}\\&=\text{3}\text{.75 V}\end{align*}[/latex]
   3. The current through all the resistors is [latex]\scriptsize 2.5\text{ A}[/latex]. (The current is the same through series combinations of resistors and you can consider the entire parallel set of resistors as one series resistor.)
      Using this, find the current through [latex]\scriptsize {{R}_{2}}[/latex].
      First find the voltage across the parallel combination:
      [latex]\scriptsize \begin{align*}V&=IR\\&=\text{2,5 x 0}\text{.5}\\&=\text{1}\text{.25 V}\end{align*}[/latex]
      Now find the current through [latex]\scriptsize {{R}_{2}}[/latex] using the fact that the voltage is the same across each resistor in the parallel combination:
      [latex]\scriptsize \begin{align*}I&=\displaystyle \frac{V}{R}\\&=\displaystyle \frac{{1.25}}{1}\\&=\text{1}\text{.25 A}\end{align*}[/latex]
4. The unknown resistor is arranged in a Wheatstone bridge with two known resistors and a rheostat (variable resistor). The variable resistor is adjusted until the voltmeter in the Wheatstone bridge reads [latex]\scriptsize 0[/latex] (reaches the balance point). The value of the unknown resistor can then be calculated using the formula:
   [latex]\scriptsize {{R}_{x}}:{{R}_{3}}={{R}_{2}}:{{R}_{1}}[/latex]
5. .
   [latex]\scriptsize \begin{align*}{{R}_{x}}:{{R}_{3}}&={{R}_{2}}:{{R}_{1}}\\\displaystyle \frac{{{{R}_{x}}}}{9}&=\displaystyle \frac{4}{2}\\{{R}_{x}}&=\text{ 18 }\Omega \end{align*}[/latex]

Back to Unit 3: Assessment